From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 19: |
Line 19: |
| | the g(y) distribution, but the drawback is that you have to generate two numbers, now one. This method will also work if the g(y) function is not a proper probability distribution (it even does not need to be normalized - every function you can always normalize). This allows for a very broad application of the von Neumann method - also to calculate definite integrals, when their analytical form does not exist. This is a typical example of a Monte Carlo method. | | the g(y) distribution, but the drawback is that you have to generate two numbers, now one. This method will also work if the g(y) function is not a proper probability distribution (it even does not need to be normalized - every function you can always normalize). This allows for a very broad application of the von Neumann method - also to calculate definite integrals, when their analytical form does not exist. This is a typical example of a Monte Carlo method. |
| | | | |
| - | Należy stworzyć trzy '''bardzo podobne''' funkcje przyjmujące obiekt typu <code>TF1</code>. Powinny one przyjmować funkcję g na przedziale [min,max]:
| + | Please prepare thee '''very similar''' functions taking as argument an object of type <code>TF1</code>. The arguments should be the function g and the range [min,max]: |
| - | * <code>double losujVonNeumann(TF1 *g, double min, double max)</code> - funkcja zwraca ''jedną'' liczbę pseudolosową z funkcji g(y), | + | * <code>double generateVonNeumann(TF1 *g, double min, double max)</code> - function returning a generated pseudo random number from distribution g(y), |
| - | * <code>double wydajnoscVonNeumann(TF1 *g, double min, double max, int n)</code> - funkcja zwraca wydajność metody akceptacji i odrzucania von Neumanna dla danej funkcji g(y) oraz zadanej liczby losowań n, | + | * <code>double efficiencyVonNeumann(TF1 *g, double min, double max, int n)</code> - function returning the efficiency of the von Neumann method for a given g(y) function and the number of generations n, |
| - | * <code>double calkaVonNeumann(TF1 *g, double min, double max, int n)</code> - funkcja zwraca całkę oznaczoną (pole powierzchni pod krzywą) z funkcji g(y) na przedzialne [min,max] przy liczbie losowań n. | + | * <code>double integra;VonNeumann(TF1 *g, double min, double max, int n)</code> - function returning the definite integral (area under the curve) from function g(y) in the range [min,max] with the number of generations n. |
| | | | |
| | ''Część trzecia:'' '''metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą''' (1 pkt.) | | ''Część trzecia:'' '''metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą''' (1 pkt.) |
Revision as of 11:43, 11 April 2022
Exercise
Part one: estimation of the Pi (1 pkt.)
Please write a function which estimates the number Pi with the von Neumann (it is arguably one of the most simple examples of the use-case of a Monte Carlo method). In order to calculate the Pi, we randomly generate two numbers x and y from the uniform distribution [0,1] and we check whether the pair falls within the circle of the radius equal to 1. Next, by calculating the ratio of accepted pairs to all of them, you approximate the ratio of areas of the circle to the rectangle. By performing such a random generation, calculate the Pi number. In addition, draw the graph of the resulted points inside and outside the circle:
- create two objects of type
TGraph and fill one of them with accepted pairs (x,y), the second one with rejected pairs. Both plots draw on one canvas,
- in addition, you can create a
TH1D object and fill it with accepted values of x. It will be a distribution of the circle.
Part two: generation of pseudo random numbers from a any probability distribution using the acceptance rejection method of von Neumann (3 pkt.)
The transformation method used a week ago has limited applications. You can do this when the analytical form of the cumulative function and its inverse function are known. The von Neumann method of generation of pseudo random numbers will work when you know only
the g(y) distribution, but the drawback is that you have to generate two numbers, now one. This method will also work if the g(y) function is not a proper probability distribution (it even does not need to be normalized - every function you can always normalize). This allows for a very broad application of the von Neumann method - also to calculate definite integrals, when their analytical form does not exist. This is a typical example of a Monte Carlo method.
Please prepare thee very similar functions taking as argument an object of type TF1. The arguments should be the function g and the range [min,max]:
-
double generateVonNeumann(TF1 *g, double min, double max) - function returning a generated pseudo random number from distribution g(y),
-
double efficiencyVonNeumann(TF1 *g, double min, double max, int n) - function returning the efficiency of the von Neumann method for a given g(y) function and the number of generations n,
-
double integra;VonNeumann(TF1 *g, double min, double max, int n) - function returning the definite integral (area under the curve) from function g(y) in the range [min,max] with the number of generations n.
Część trzecia: metoda akceptacji i odrzucania von Neumanna z funkcją pomocniczą (1 pkt.)
W celu zwiększenia wydajności metody von Neumanna, można posłużyć się ograniczeniem przedziału losowania w postacji zadanej funkcji pomocniczej. W tej części zaimplementować funkcję, która oblicza całkę z funkcji g(y) metodą akceptacji i odrzucania von Neumanna z funkcją pomocniczą s(y):
-
double calkaVonNeumannZPomoc(TF1 *g, TF1 *s, double min, double max, int n, double &wydajnosc) - zwraca całkę na przedziale [min,max] oraz dla zadanej liczby losowań n. Ponadto, funkcja powinna zwrócić przez referencję (ponieważ w języku C/C++ funkcja nie może zwrócić dwóch wartości) wydajność tej metody.
Funkcję s(y) dobieramy tak, by zawsze znajdowała się powyżej funkcji g(y) i można z niej było łatwo wygenerować liczbę pseudolosową (na przykład metodą transformacji rozkładu jednorodnego z wykorzystaniem odwrotności dystrybuanty; na wykładzie przykład z funkcją liniową).
Wszystkie obliczenia należy wykonać dla funkcji typu:
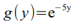
Uwagi
- Czytamy dokładnie Wykład 5 link slajdy 9-19
- Do generowania liczb z rozkładu jednorodnego używamy funkcji
Uniform z klasy TRandom lub generatora napisanego w poprzednim zadaniu
- Pamiętajmy, że zawsze akceptujemy wylosowane punkty pod zadaną krzywą w stosunku do wszystkich wylosowanych (stosunek ten ma się do siebie (dla N dążących do nieskończoności) jak stosunki powierzchni obszarów wewnątrz których zostało dokonane losowanie)
- Jako funkcję pomocniczą przyjmujemy funkcję liniową.
- W przypadku całkowania z wykorzystaniem funkcji pomocniczej zawsze dobieramy ją w taki sposób, aby można było wygenerować liczbę z jej rozkładu w łatwy sposób (za pomocą odwracania dystrybuanty) - innymi słowy, zamieniamy prostokąt (dwa rozkłady jednorodne) na inny obszar, wewnatrz którego dokonujemy losowań (musimy umieć wylosować liczby z tego obszaru)
- Funkcja kwadratowa i jej odwrotność:
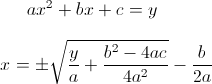
Results
Part one
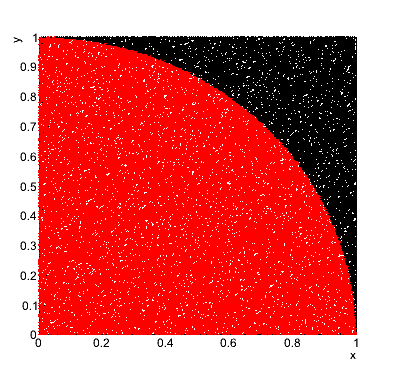
Output:
The Pi number equals: 3.14392
Parts two and three
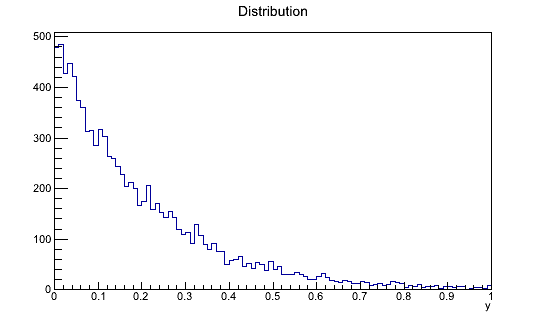
Output:
Integral: 0.199
Efficiency: 0.2072
Integral (method with the helper function): 0.198745
Efficiency (method with the helper function): 0.39749
Integral calculated using the ROOT method Integral: 0.198652