Sformułowana przez Prigogine'a zasada minimum produkcji entropii głosi, że układy w okolicach stanu równowagi przechodzą przez stany (nierównowagowe), w których produkcja entropii jest najmniejsza.
Niech P będzie produkcją entropii,
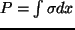 , gdzie
, gdzie 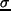 jest objętościową produkcją entropii. W układzie, gdzie występuje różnica temperatur, następuje przepływ ciepła związany z produkcją entropii. Można to zapisać jako:
jest objętościową produkcją entropii. W układzie, gdzie występuje różnica temperatur, następuje przepływ ciepła związany z produkcją entropii. Można to zapisać jako:
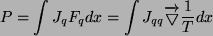 |
(16) |
gdzie 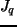 jest prądem ciepła, proporcjonalnym do siły termodynamicznej
jest prądem ciepła, proporcjonalnym do siły termodynamicznej 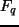 ze współczynnikiem proporcjonalności Onsagera. Prawą stronę możemy zapisać w przypadku jednowymiarowym jako:
ze współczynnikiem proporcjonalności Onsagera. Prawą stronę możemy zapisać w przypadku jednowymiarowym jako:
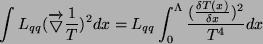 |
(17) |
gdzie 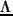 jest wielkościa układu.
jest wielkościa układu.
T(x) jest nieznaną funkcją rozkładu temperatury w układzie. Jeżeli chcemy znaleźć minimum produkcji entropii w tym układzie, musimy zastosować metodę rachunku wariacyjnego (zasada najmniejszego działania w Mechanice Teoretycznej). Oznaczmy minimalizowany funkcjonał:
![\begin{displaymath}W[T(x)] = L_{qq}\int_0^\Lambda \frac{(\frac{\delta T(x)}{\delta x})^2}{T^4} dx \end{displaymath}](img38.png) |
(18) |
Wtedy:
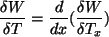 |
(19) |
gdzie
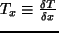 . Wykażemy, że zasada minimum produkcji entropii prowadzi do wniosku, że ciepło ma stały strumień:
. Wykażemy, że zasada minimum produkcji entropii prowadzi do wniosku, że ciepło ma stały strumień:
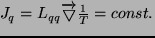 Z zasady najmniejszego działania mamy:
Z zasady najmniejszego działania mamy:
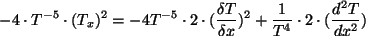 |
(20) |
Po przemnożeniu przez 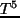 i uporządkowaniu otrzymujemy:
i uporządkowaniu otrzymujemy:
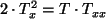 |
(21) |
Z kolei różniczkując po T stałe (z założenia) wyrażenie:
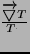 otrzymujemy:
otrzymujemy:
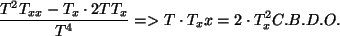 |
(22) |
Zasada minimum produkcji entropii doprowadziła do wniosku, że strumień ciepła musi być stały czyli ciepło nie jest magazynowane w obszarze przepływu. Wniosek ten jest analogiczny do zasady zachowania ładunku.
Przykład:
Jeżeli mamy dwa sprzężone strumienie: 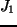 i
i 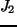 , takie, że:
, takie, że:
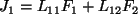 |
(23) |
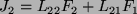 |
(24) |
Produkcja entropii jest:
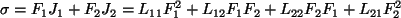 |
(25) |
Niech 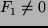 będzie ustalone,
będzie ustalone, 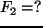 Z zasady minimum produkcji entropii mamy:
Z zasady minimum produkcji entropii mamy:
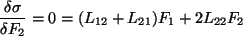 |
(26) |
Dodatkowo założymy, że 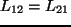 i wtedy:
i wtedy:
![\begin{displaymath}0=2\cdot [L_{12}F_1+L_{22}F_2] = 2J_2\end{displaymath}](img56.png) |
(27) |
czyli, jeżeli działamy w układzie sprzężonym siłą termodynamiczną, a druga siła ma się "dopasować", aby spełniona była zasada minimalnej produkcji entropii, to dopasowanie polega na tym, że strumień tej wielkości 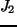 musi być równy zero. Z równania tego mamy też:
musi być równy zero. Z równania tego mamy też:
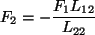 |
(28) |
Tego typu zależność opisuje np. efekt Peltiera lub Seebecka.
Dorota Cieleń
2004-01-22
![]() będzie ustalone,
będzie ustalone, ![]() Z zasady minimum produkcji entropii mamy:
Z zasady minimum produkcji entropii mamy: