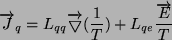Prawa termodynamiki nierównowagowej.

$$\overrightarrow J_q=L_{qq}\overrightarrow \bigtriangledown (\frac{1}{T})+L_{qe}\frac{\overrightarrow E}{T}$$ (1)

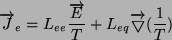$$\overrightarrow J_e=L_{ee}\frac {\overrightarrow E}{T} +L_{eq}\overrightarrow \bigtriangledown (\frac{1}{T})$$ (2)

Korzystając z tych praw wyprowadzimy wyrażenia na współczynniki Onsagera. a. Zakładamy, że rozpatrujemy tylko siłę termodynamiczną 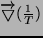$\overrightarrow \bigtriangledown (\frac{1}{T})$ - przepływ ciepła następuje pod wpływem gradientu temperatury. Wtedy:

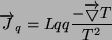$$\overrightarrow J_q = Lqq \frac{-\overrightarrow \bigtriangledown T}{T^2}$$ (3)

Z termodynamiki klasycznej wiemy, że przepływ ciepła 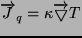$\overrightarrow J_q = \kappa \overrightarrow \bigtriangledown T$, gdzie 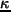$\kappa$ jest współczynnikiem przewodnictwa cieplnego. Otrzymujemy więc:

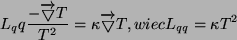$$L_qq \frac{-\overrightarrow \bigtriangledown T}{T^2}=\kappa \... ...arrow \bigtriangledown T, \qquad wiec \qquad L_{qq}=\kappa T^2$$ (4)

b. Zakładamy, że działa tylko siła elektryczna, 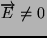$\overrightarrow E \neq 0$. Mamy więc:

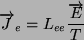$$\overrightarrow J_e = L_{ee}\frac{\overrightarrow E}{T}$$ (5)

Ponieważ gęstość prądu $\overrightarrow J_e$ związana jest z natężeniem pola przez równanie: 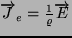$\overrightarrow J_e = \frac{1}{\varrho } \overrightarrow E$, gdzie 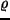$\varrho$ jest opornością właściwą, a 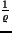$\frac{1}{\varrho }$ to współczynnik przewodnictwa elektrycznego, to otrzymujemy:

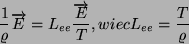$$\frac{1}{\varrho } \overrightarrow E = L_{ee} \frac{\overrightarrow E}{T}, \qquad wiec \qquad L_{ee}=\frac{T}{\varrho }$$ (6)

c. Efekt Seebecka. (RYSUNEK)

Jeżeli założymy, że opór voltomierza jest nieskończony, 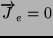$\overrightarrow J_e=0$ i korzystając ze wzoru (2) otrzymujemy:

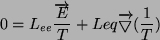$$0=L_{ee}\frac{\overrightarrow E}{T}+L{eq}\overrightarrow \bigtriangledown (\frac{1}{T})$$ (7)

Warunek ten musi być spełniony w każdym punkcie układu, czyli

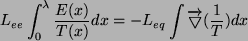$$L_{ee}\int_0^\lambda \frac{E(x)}{T(x)} dx = - L_{eq}\int \overrightarrow \bigtriangledown (\frac{1}{T})dx$$ (8)

Uśredniając temperaturę i korzystając z zależności 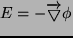$E=-\overrightarrow \bigtriangledown \phi$ otrzymujemy:

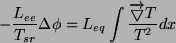$$-\frac{L_{ee}}{T_{sr}}\Delta \phi = L_{eq} \int \frac{\overrightarrow \bigtriangledown T}{T^2}dx$$ (9)

i prawą stronę w przybliżeniu można zapisać jako:

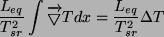$$\frac {L_{eq}}{T_{sr}^2}\int \overrightarrow \bigtriangledown T dx = \frac{L_{eq}}{T_{sr}^2} \Delta T$$ (10)

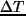gdzie $\Delta T$ oznacza różnicę temperatur. Zatem:

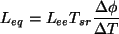$$L_{eq} = L_{ee} T_{sr} \frac {\Delta \phi}{\Delta T}$$ (11)

Otrzymujemy w ten sposób wzór łączący 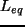$L_{eq}$ z wielkościami mierzalnymi $(\frac{\Delta \phi}{\Delta T})$.

d. Efekt Peltiera. (RYSUNEK)

Ponieważ złącza są w jednakowej temperaturze, to 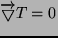$\overrightarrow \bigtriangledown T=0$, stąd korzystając ze wzoru (1) i (2):

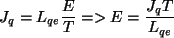$$J_q = L_{qe}\frac{E}{T} \qquad => \qquad E= \frac {J_q T }{L_{qe}}$$ (12)

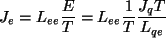$$J_e = L_{ee}\frac{E}{T} \qquad = \qquad L_{ee} \frac{1}{T} \frac {J_q T}{L_{qe}}$$ (13)

czyli :

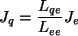$$J_q = \frac {L_{qe}}{L_{ee}} J_e$$ (14)

Pomimo równych temperatur złącz w układzie następuje przepływ ciepła, proporcjonalny do prądu w tym układzie. Widać też, że:

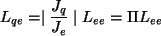$$L_{qe} = \mid \frac{J_q}{J_e}\mid L_{ee} = \Pi L_{ee}$$ (15)

gdzie 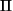$\Pi$ - ciepło Peltiera, zdefiniowany jako strumień ciepła wydzielany w układzie na skutek przepływu prądu elektrycznego o jednostkowym natężeniu.