KADD laboratorium 2

From MJanik

Revision as of 13:29, 9 March 2012 (view source) Majanik (Talk | contribs) (Created page with "Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x): <!--<math>f(x,y)=c\,e^{-(x^{2}+4y^{2}-2xy)}</math> --> <math>f(x,y)=\left\lbrace \begin{array}{ll} c\,...") ← Older edit		Latest revision as of 11:06, 14 March 2012 (view source) Majanik (Talk | contribs)
(3 intermediate revisions not shown)
Line 1:		Line 1:
		+	== Zadanie ==
		+
	Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x):		Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x):
	<!--<math>f(x,y)=c\,e^{-(x^{2}+4y^{2}-2xy)}</math> -->		<!--<math>f(x,y)=c\,e^{-(x^{2}+4y^{2}-2xy)}</math> -->
		+	[[File:Wzor.png]]
-	<math>f(x,y)=\left\lbrace \begin{array}{ll} c\,\cos(\frac{1}{2}x)\sin(y),&0\leqslant x\leqslant \pi \,\wedge\, 0\leqslant y\leqslant \pi\\0,&\text{pozostale przypadki}\end{array}\right. </math>
-		+	Należy:
-		+
-	Należy dla parametru a=6:	+
	* Narysować gęstość prawdopodobieństwa f(x) (0.5 pkt)		* Narysować gęstość prawdopodobieństwa f(x) (0.5 pkt)
	* Narysować dystrybuantę F(x). Dystrybuantę należy obliczyć analitycznie oraz numerycznie (1 pkt)		* Narysować dystrybuantę F(x). Dystrybuantę należy obliczyć analitycznie oraz numerycznie (1 pkt)
Line 19:		Line 19:
	** mediana		** mediana
	** kwartyl górny		** kwartyl górny
		+
		+
		+	== Wynik ==
		+	[[File:lab22.png]]
		+
		+	P(0.2<=X<=0.5): 0.280756
		+
		+	E(X): numerycznie=0.570796
		+
		+	var(X): numerycznie=0.141593 analityczne=0.141593
		+
		+	moda=0
		+
		+	kwartyl 0.25: 0.25268
		+
		+	kwartyl 0.5: 0.523599
		+
		+	kwartyl 0.75: 0.848062

---

Latest revision as of 11:06, 14 March 2012

Zadanie

Niech X będzie zmienną losową o gęstości prawdopodobieństwa f(x):

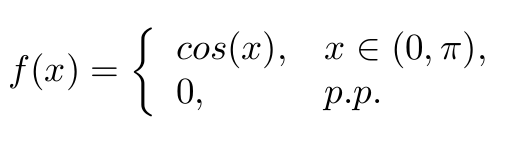
Należy:

• Narysować gęstość prawdopodobieństwa f(x) (0.5 pkt)
• Narysować dystrybuantę F(x). Dystrybuantę należy obliczyć analitycznie oraz numerycznie (1 pkt)
• Obliczyć prawdopodobieństwo P(5 <= X \<= 10) (0.5 pkt)
• Obliczyć wartość oczekiwaną E(X) oraz porównać z wynikiem analitycznym (1 pkt)
• Obliczyć wariancję V(X) oraz porównać z wynikiem analitycznym (1 pkt)
• Wyznaczyć mode rozkładu (0.5 pkt)
• Wyznaczyć kwantyle: (0.5 pkt)
  • kwartyl dolny
  • mediana
  • kwartyl górny

Wynik

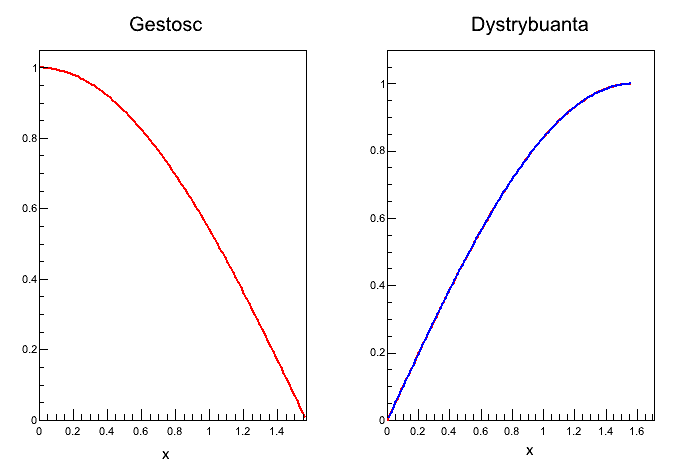
P(0.2<=X<=0.5): 0.280756

E(X): numerycznie=0.570796

var(X): numerycznie=0.141593 analityczne=0.141593

moda=0

kwartyl 0.25: 0.25268

kwartyl 0.5: 0.523599

kwartyl 0.75: 0.848062