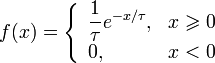From Łukasz Graczykowski
Exercise
Part one: linear congruent generator of pseudorandom numbers (1 pkt.)
Please write a generator of pseudorandom numbers and save generated numbers into a file.
The generator should be based on the following formula:
x[j+1] = (g*x[j] + c) mod m.
This generator is called LCG - linear congruent generator. Providing the first (beginning) number x[0] defines the whole series, which is periodic. The period depends on the parameters and under certain conditions it reaches maximum value of m. These conditions are:
-
c and m do not have joint divisors,
-
b = g-1 is a multiply of every prime number p, which is a divisor of a number m,
-
b is a multiply of 4 if n is also a multiply of 4.
For simplicity we can uuse c = 0, and in that case we get a multiplicative generator (MLCG).
- Value of
g and m should be easy to modify in the program.
The result of the macro execution should be a file with the name name.dat containing a series of generated numbers for a given set of parameters. The macro should be executed three times, resulting in three files: random1.dat, random2.dat, random3.dat, for the following parameters, respectively:
-
m=97 i g=23,
-
m=32363 i g=157,
-
m=147483647 i g=16807.
Second part: spectral test (1 pkt.)
Please perform a spectral test to see what is the quality of the generator. In order to do so please draw plot on the (x[n], x[n+1]) points from generated numbers. The obtained graph will show a spectral pattern of the generator - hence the name of the test.
If the points are distributed uniformly, the test can be judged good. If they show a certain periodic pattern - the test doesn't work properly. Of course, for the position of the points what maters are the parameters g and m.
- In order to draw spectral test, please use
TH2D.
As a result, we should have three spectral tests.
Część trzecia: generacja liczb losowych oparta na transformacji rozkładu jednorodnego (3 pkt.)
Dowolna funkcja zmiennej losowej jest zmienną losową. Powstaje więc pytanie jaka jest gęstość zmiennej losowej Y jeżeli znana jest gęstość f(x). Zakładamy, że prawdopodobieństwo g(y)dy jest równe f(x)dx, gdzie dx odpowiada wartością dy. Warunek jest spełniony dla odpowiednio małych dx. Wynika stąd, że:
g(y) = dx/dy f(x)
Teraz jeżeli założymy, że gęstość prawdopodobieństwa f(x) wynosi 1 w 0<=x<=1 i f(x) = 0 dla x<= 0 i x>1 to powyższe równanie możemy zapisać w postaci:
g(y)dy = dx = dG(y),
gdzie G(y) jest dystrybuantą zmiennej losowej Y. Co po całkowaniu daje nam
x = G(y) => y = G^-1(x).
Jeśli zmienna losowa X ma rozkład jednostajny na odcinku pomiędzy 0 i 1 oraz jeśli znana jest funkcja odwrotna G^-1(x) to funkcja g(y) opisuje gęstość prawdopodobieństwa rozkładu zmiennej losowej Y.
Używając tej metody należy wygenerować 10000 liczb z rozkładu:
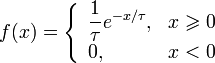
Dla tau = 2:
- Należy wygenerować 10000 liczb z rozkładu 0 do 1 używając generatora z części pierwszej (zapisać do pliku wartości xn makrem z pierwszej części a następnie je wczytać w makrze z części drugiej).
- Analitycznie (na kartce) policzyć dystrybuantę tego rozkładu, a następnie funkcję odwrotną. (1 pkt.)
- Wygenerować rozkład
f(x) - wrzucając wygenerowane wartości do histogramu - korzystając z: (1 pkt.)
- liczb wygenerowanych wcześniej i wczytanych z plików
losowe1.dat, losowe2.dat, losowe3.dat,
- standardowego generatora ROOT'a, np.
gRandom->Uniform(1) (obiekt gRandom istnieje domyślnie w uruchomionej instancji ROOT; można oczywiście również stworzyć samodzielnie obiekt TRandom - link).
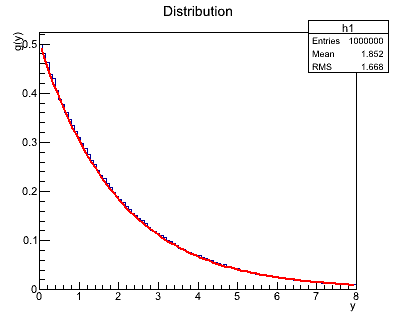
- Narysować na jednym wykresie histogram (odpowiednio unormowany) oraz funkcję teoretyczną
f(x) (obiekt TF1). (1 pkt.)
Uwagi
- Czytamy dokładnie Wykład 4 (link), zwłaszcza slajdy 6 oraz 18-25
- Na samym początku, przed losowaniem, musimy samodzielnie ustawić wartość pierwszej liczby pseudolosowej x0 (tzw. ziarno, "seed"). Jeżeli chcemy, by za każdym razem liczby pseudolosowe były inne, możemy je ustawić z zegara systemowego:
x0 = time(NULL);
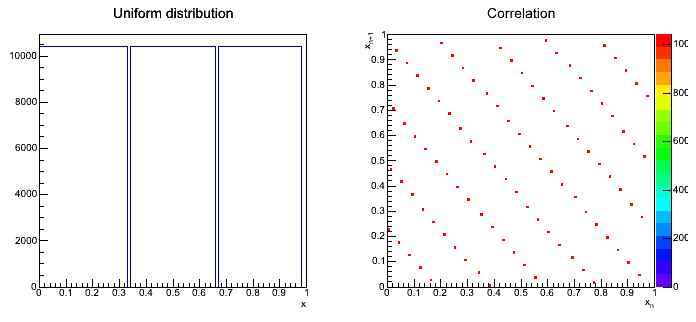
- Parametry histogramów z obrazków poniżej:
TH1D *hUniform = new TH1D("hUniform","Uniform distribution",100,0,1);
TH2D *hCorr = new TH2D("hCorr","Correlation",100,xmin,xmax,100,0,1);
- Ilość losowań w części pierwszej:
const int N = 1000000;
- Wczytywanie danych z pliku:
ifstream ifile;
ifile.open("dane.dat");
double val;
while(ifile>>val)
{
cout<<val<<endl;
}
ifile.close();
- Zapisywanie danych do pliku:
ofstream ofile;
ofile.open("dane.dat");
for(int i=0;i<N;i++)
ofile<<val<<endl;
}
ofile.close();
Wynik
Przykładowy rozkład dla parametrów:
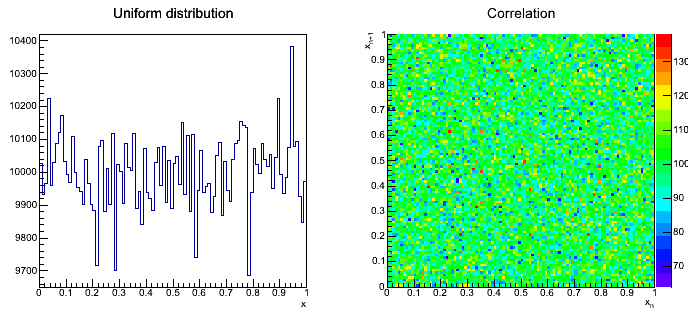
Przykładowy wynik transformacji rozkładu jednorodnego: