From Łukasz Graczykowski
(Difference between revisions)
|
|
| (11 intermediate revisions not shown) |
| Line 2: |
Line 2: |
| | '''Weryfikacja hipotez statystycznych''' (5 pkt.) | | '''Weryfikacja hipotez statystycznych''' (5 pkt.) |
| | | | |
| - | * Przeprowadzono eksperyment naświetlania wodorowej komory pęcherzykowej wiązką fotonów w celu badania oddziaływań fotonów z protonami. Fotony powodują powstawanie par elektron-pozyton, które mogą być wykorzystane do monitorowania wiązki fotonów. Częstość występowania zdjęć z 0,1,2,... parami elektron-pozyton powinna podlegać rozkładowi Poissona. Należy wczytać dane z [http://www.if.pw.edu.pl/~lgraczyk/KADD2016/lab10/dane10.txt pliku] (w pierwszej kolumnie znajduje się liczba par elektronowych na zdjęciu <code>k</code>, a w drugiej liczba zdjęć zawierających <code>k</code> par elektronowych). Widzimy, że rozkład ten przypomina rozkład Poissona - próbujemy zatem obliczyć estymator największej wiarygodności dla parametry rozkładu Poissona (patrz [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad10-2019.pdf Wykład 10] slajd 13) (1 pkt.) | + | * Przeprowadzono eksperyment naświetlania wodorowej komory pęcherzykowej wiązką fotonów w celu badania oddziaływań fotonów z protonami. Fotony powodują powstawanie par elektron-pozyton, które mogą być wykorzystane do monitorowania wiązki fotonów. Częstość występowania zdjęć z 0,1,2,... parami elektron-pozyton powinna podlegać rozkładowi Poissona. Należy wczytać dane z [http://www.if.pw.edu.pl/~lgraczyk/KADD2016/lab10/dane10.txt pliku] (w pierwszej kolumnie znajduje się liczba par elektronowych na zdjęciu <code>k</code>, a w drugiej liczba zdjęć zawierających <code>k</code> par elektronowych). Widzimy, że rozkład ten przypomina rozkład Poissona - próbujemy zatem obliczyć estymator największej wiarygodności dla parametry rozkładu Poissona (patrz [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad11-2019.pdf Wykład 11] slajd 14) (1 pkt.) |
| | | | |
| | * Narysować na jednym wykresie punkty pomiarowe i dopasowanie (metodą estymatora największej wiarygodności i funkcją Fit z ROOT'a użytą z parametrami "LR" - dopasowanie metodą największej wiarygodności). Funkcja TF1 do rysowania (i dopasowania ROOT'em) to TMath::PoissonI (1 pkt.) | | * Narysować na jednym wykresie punkty pomiarowe i dopasowanie (metodą estymatora największej wiarygodności i funkcją Fit z ROOT'a użytą z parametrami "LR" - dopasowanie metodą największej wiarygodności). Funkcja TF1 do rysowania (i dopasowania ROOT'em) to TMath::PoissonI (1 pkt.) |
| Line 25: |
Line 25: |
| | | | |
| | Wykorzystując zaimplementowaną funkcję zweryfikować hipotezę mówiacą, że dane pomiarowe podlegają rozkładowi Poissona. Dobrać odpowiednią wartość poziomu istotności. Uwaga! Kwanyl możemy odczytać z policzonej na ostatnich zajęciach dystrybuanty. (2 pkt.) | | Wykorzystując zaimplementowaną funkcję zweryfikować hipotezę mówiacą, że dane pomiarowe podlegają rozkładowi Poissona. Dobrać odpowiednią wartość poziomu istotności. Uwaga! Kwanyl możemy odczytać z policzonej na ostatnich zajęciach dystrybuanty. (2 pkt.) |
| | + | |
| | + | == Uwagi == |
| | + | * Nasze zadanie to '''ręczne''' przeprowadzenie czynności wykonywanych automatycznie przez funkcję <code>Fit</code>. |
| | + | * Zadanie zawiera w sobie dwie części: wyznaczenie parametru rozkładu Poissona '''metodą największej wiarygodności''' (maximum likelihood), szukając '''estymatora o najniższej wariancji'''. Czytamy zatem: Wykład 9 [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad9-2019.pdf link] - o metodzie największej wiarygodności, od początku do slajdu 24 (to są części teoretyczne z wyprowadzeniami), dalej Wykład 10 [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad10-2019.pdf link] |
| | + | * Funkcja wiarygodności to ogólnie rzecz biorąc funkcja rozkładu prawdopodobieństwa dla '''parametrów''' badanego rozkładu, okreslana na podstawie próby losowej (jeżeli badamy np. rozkład wzrostu Polaków f(x), gdzie X to zmienna losowa okreslająca wzrost Polaków, np. rozkład Gaussa o dwóch parametrach (średnia, odchylenie), to L będzie funkcją wiarygodności, rozkładem prawdopodobieństwa parametrów średniej i odchylenia -> szukamy maksimum funkcji L, które da nam najbardziej wiarygodne wartości parametrów średnia i odchylenie funkcji f(x)) |
| | + | * Szukanie parametrów metodą największej wiarygodności polega na rozwiązaniu równań wiarygodności, które są niczym innym tylko warunkami koniecznymi na istnienie maksimum funkcji L (zgodnie z analizą matematyczna - liczymy odpowiednie pochodne) |
| | + | * Dla rozkładu Poissona estymator o najniższej wariancji otrzymany metodą największej wiarygodności wynika z rozwiązania równania wiarygodności (jedno równanie, bo jeden parametr Lambda) - slajd 14 na Wykładzie 11 [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad11-2019.pdf link] |
| | + | * Druga część, po znalezieniu estymatora o najniższej wiarygodności, polega na przeprowadzeniu testu chi-kwadrat. W tym celu czytamy dokładnie Wykład 11 (zwłaszcza slajdy 7-16) [http://www.if.pw.edu.pl/~lgraczyk/KADD2019/Wyklad11-2019.pdf link]. |
| | + | * Na wykresie poniżej (histogram) są dwie linie - niebieska i czerwona. Jedna z nich to dopasowanie dokonane automatycznie funkcją <code>Fit</code>, druga to ręczne dopasowanie sposeb powyżej. |
| | + | * Do rozkładu Poissona w postaci takich "schodków" stosujemy funkcję <code>TMath::PoissonI</code> ([https://root.cern.ch/root/html534/TMath.html#TMath:PoissonI link]) |
| | | | |
| | == Wynik == | | == Wynik == |
Latest revision as of 09:22, 4 May 2020
Zadanie
Weryfikacja hipotez statystycznych (5 pkt.)
- Przeprowadzono eksperyment naświetlania wodorowej komory pęcherzykowej wiązką fotonów w celu badania oddziaływań fotonów z protonami. Fotony powodują powstawanie par elektron-pozyton, które mogą być wykorzystane do monitorowania wiązki fotonów. Częstość występowania zdjęć z 0,1,2,... parami elektron-pozyton powinna podlegać rozkładowi Poissona. Należy wczytać dane z pliku (w pierwszej kolumnie znajduje się liczba par elektronowych na zdjęciu
k, a w drugiej liczba zdjęć zawierających k par elektronowych). Widzimy, że rozkład ten przypomina rozkład Poissona - próbujemy zatem obliczyć estymator największej wiarygodności dla parametry rozkładu Poissona (patrz Wykład 11 slajd 14) (1 pkt.)
- Narysować na jednym wykresie punkty pomiarowe i dopasowanie (metodą estymatora największej wiarygodności i funkcją Fit z ROOT'a użytą z parametrami "LR" - dopasowanie metodą największej wiarygodności). Funkcja TF1 do rysowania (i dopasowania ROOT'em) to TMath::PoissonI (1 pkt.)
- Sprawdzić jakość dopasowania za pomocą testu χ2. W tym celu należy zaimplementować funkcję obliczającą statystykę testową χ2 zgodnie z wzorem
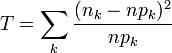
gdzie: nk - liczba obserwacji w k-tym binie, npk - przewidywana przez teorię liczba przypadków w k-tym binie tj.:
// h - histogram danych
// g - przewidywanie "teoretyczne"
double chi2(TH1D *h, TF1 *f);
- Okreslić liczbę stopni swobody i obliczyć wartość statystyki testowej. (1 pkt.)
- Zaimplementować funkcję zwracającą wynik testu χ2 na zadanym poziomie istotności α tj.:
// true - brak podstaw do odrzucenia hipotezy
// false - sa podstawy do odrzucenia hipotezy
// Parametry:
// T - wartosc statystyki testowej chi2
// alpha - poziom istotnosci
// ndf - liczba stopni swobody rozkladu chi2
bool testChi2(double T, double alpha, int ndf);
Wykorzystując zaimplementowaną funkcję zweryfikować hipotezę mówiacą, że dane pomiarowe podlegają rozkładowi Poissona. Dobrać odpowiednią wartość poziomu istotności. Uwaga! Kwanyl możemy odczytać z policzonej na ostatnich zajęciach dystrybuanty. (2 pkt.)
Uwagi
- Nasze zadanie to ręczne przeprowadzenie czynności wykonywanych automatycznie przez funkcję
Fit.
- Zadanie zawiera w sobie dwie części: wyznaczenie parametru rozkładu Poissona metodą największej wiarygodności (maximum likelihood), szukając estymatora o najniższej wariancji. Czytamy zatem: Wykład 9 link - o metodzie największej wiarygodności, od początku do slajdu 24 (to są części teoretyczne z wyprowadzeniami), dalej Wykład 10 link
- Funkcja wiarygodności to ogólnie rzecz biorąc funkcja rozkładu prawdopodobieństwa dla parametrów badanego rozkładu, okreslana na podstawie próby losowej (jeżeli badamy np. rozkład wzrostu Polaków f(x), gdzie X to zmienna losowa okreslająca wzrost Polaków, np. rozkład Gaussa o dwóch parametrach (średnia, odchylenie), to L będzie funkcją wiarygodności, rozkładem prawdopodobieństwa parametrów średniej i odchylenia -> szukamy maksimum funkcji L, które da nam najbardziej wiarygodne wartości parametrów średnia i odchylenie funkcji f(x))
- Szukanie parametrów metodą największej wiarygodności polega na rozwiązaniu równań wiarygodności, które są niczym innym tylko warunkami koniecznymi na istnienie maksimum funkcji L (zgodnie z analizą matematyczna - liczymy odpowiednie pochodne)
- Dla rozkładu Poissona estymator o najniższej wariancji otrzymany metodą największej wiarygodności wynika z rozwiązania równania wiarygodności (jedno równanie, bo jeden parametr Lambda) - slajd 14 na Wykładzie 11 link
- Druga część, po znalezieniu estymatora o najniższej wiarygodności, polega na przeprowadzeniu testu chi-kwadrat. W tym celu czytamy dokładnie Wykład 11 (zwłaszcza slajdy 7-16) link.
- Na wykresie poniżej (histogram) są dwie linie - niebieska i czerwona. Jedna z nich to dopasowanie dokonane automatycznie funkcją
Fit, druga to ręczne dopasowanie sposeb powyżej.
- Do rozkładu Poissona w postaci takich "schodków" stosujemy funkcję
TMath::PoissonI (link)
Wynik
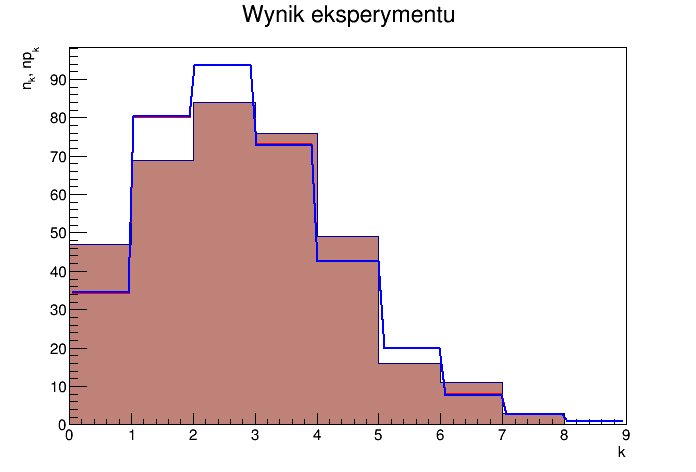
Output:
FCN=5.75356 FROM MIGRAD STATUS=CONVERGED 29 CALLS 30 TOTAL
EDM=5.17016e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 3.55268e+02 1.88558e+01 3.25727e-02 3.68816e-05
2 p1 2.33737e+00 8.17264e-02 1.40382e-04 -2.26405e-03
ERR DEF= 0.5
Lambda najwiekszej wiarygodnosci: 2.33239
Lambda (ROOT Fit): 2.33737
chi2 (wartosc statystyki testowej T): 10.5336
chi2/NDF: 1.7556
chi2 (ROOT Fit): 9.85507
chi2 (ROOT Fit)/NDF: 1.40787
Poziom istotnosci alpha: 0.01
Wynik testu: nie ma podstaw do odrzucenia hipotezy