From Łukasz Graczykowski
(Difference between revisions)
|
|
| (6 intermediate revisions not shown) |
| Line 35: |
Line 35: |
| | ifile.close(); | | ifile.close(); |
| | | | |
| - | * Do wszystkich operacji na macierzach (tworzenie macierzy kowariancji, mnożenie macierzy, transponowanie macierzy) - polecana jest klasa '''<code>TMatrixD</code>''' | + | * Do wszystkich operacji na macierzach (tworzenie macierzy kowariancji, mnożenie macierzy, transponowanie macierzy) - polecana jest klasa '''<code>TMatrixD</code>''' [https://root.cern.ch/root/html534/TMatrixT_double_.html link] |
| | + | * '''Pamiętajcie, że w przypadku działań na macierzach (mnożenie) kolejność jest ważna (mnożenie macierzy nie jest przemienne).''' |
| | + | * Niepewności oraz wsp. korelacji wielkości X określamy z histogramów TH2D po wczytaniu danych, niepewności oraz wsp. korelacji wielkości Y określamy z macierzy kowariancji wielkości Y |
| | + | * '''Granice przedziałów na osiach oraz liczba binów w histogramach TH2D (w moim rozwiazaniu): |
| | + | |
| | + | double x1min = 1.5, x1max = 5.0; |
| | + | double x2min = 0.0, x2max = 3.0; |
| | + | double x3min = 4.0, x3max = 16.0; |
| | + | TH2D *h12 = new TH2D("h12","Hist12",100,x1min,x1max,100,x2min,x2max); |
| | + | TH2D *h13 = new TH2D("h13","Hist13",100,x1min,x1max,100,x3min,x3max); |
| | + | TH2D *h23 = new TH2D("h13","Hist23",100,x2min,x2max,100,x3min,x3max); |
| | + | |
| | * [http://pl.wikibooks.org/wiki/Statystyka_matematyczna/Momenty_statystyczne_w_dzia%C5%82aniu Wikibooks] | | * [http://pl.wikibooks.org/wiki/Statystyka_matematyczna/Momenty_statystyczne_w_dzia%C5%82aniu Wikibooks] |
| | | | |
Latest revision as of 09:08, 23 March 2020
Zadanie
Wykonano pomiary trzech wielkości fizycznych X1, X2 oraz X2. Wyniki pomiarów znajdują się w plikach: Dane1.dat, Dane2.dat oraz Dane3.dat.
- Należy określić wynik pomiaru (średnia oraz niepewność - odchylenie standardowe) tych wielkości oraz narysować wykresy zależności między zmiennymi
(X1, X2), (X2, X3) oraz (X1, X3). (1 pkt)
Wielkości fizyczne Y1, Y2 związane są z wielkościami X1, X2, X3 następującymi relacjami:
Y1 = 2 X1 + 5 X2 + X3
Y2 = 3 + 0.5 X1 + 4 X2
Należy wyznaczyć:
- macierz kowariancji zmiennych X1, X2, X3 (1 pkt)
- zmierzone wartości średnie zmiennych Y1, Y2 w pomiarze pośrednim (0.5 pkt)
- macierz kowariancji zmiennych Y1, Y2 (1pkt)
- błędy z jakimi zmierzono pośrednio wielkości Y1, Y2 (1 pkt)
- wpółczynnik korelacji pomiędzy zmiennymi Y1 i Y2 (0.5 pkt)
Uwagi
- Obejrzeć dokładnie trzy pierwsze slajdy z Wykładu 5 link
- Szczegółowy opis slajdy 12-16 na wykładzie 4 link
- Wczytywanie danych z pliku (tak samo jak w języku C++):
ifstream ifile;
ifile.open("dane.dat");
double val;
while(ifile>>val)
{
cout<<val<<endl;
}
ifile.close();
- Do wszystkich operacji na macierzach (tworzenie macierzy kowariancji, mnożenie macierzy, transponowanie macierzy) - polecana jest klasa
TMatrixD link
- Pamiętajcie, że w przypadku działań na macierzach (mnożenie) kolejność jest ważna (mnożenie macierzy nie jest przemienne).
- Niepewności oraz wsp. korelacji wielkości X określamy z histogramów TH2D po wczytaniu danych, niepewności oraz wsp. korelacji wielkości Y określamy z macierzy kowariancji wielkości Y
- Granice przedziałów na osiach oraz liczba binów w histogramach TH2D (w moim rozwiazaniu):
double x1min = 1.5, x1max = 5.0;
double x2min = 0.0, x2max = 3.0;
double x3min = 4.0, x3max = 16.0;
TH2D *h12 = new TH2D("h12","Hist12",100,x1min,x1max,100,x2min,x2max);
TH2D *h13 = new TH2D("h13","Hist13",100,x1min,x1max,100,x3min,x3max);
TH2D *h23 = new TH2D("h13","Hist23",100,x2min,x2max,100,x3min,x3max);
Wynik
Wykresy:
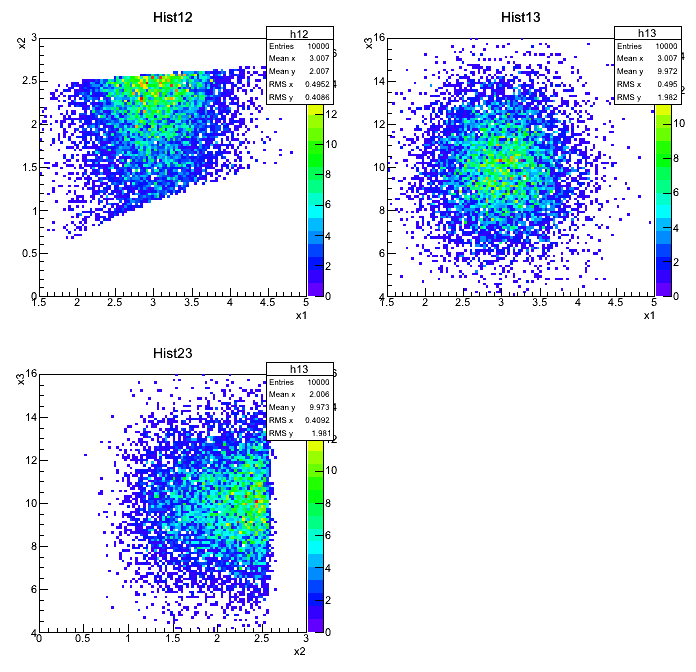
Output:
X1=3.00691, u(X1)=0.495242
X2=2.00581, u(X1)=0.40909
X3=9.97287, u(X3)=1.98102
rho(X1,X2)=0.156132
rho(X1,X3)=-0.00698853
rho(X2,X3)=0.00875851
po zakragleniu do 2 cyfr znaczacych:
X1=3.01, u(X1)=0.50
X2=2.01, u(X1)=0.41
X3=9.97, u(X3)=1.98
To jest macierz kowariancji wielkosci X
3x3 matrix is as follows
| 0 | 1 | 2 |
--------------------------------------------
0 | 0.2453 0.0316 -0.006855
1 | 0.0316 0.1674 0.0071
2 | -0.006855 0.0071 3.924
To jest macierz kowariancji wielkosci Y
2x2 matrix is as follows
| 0 | 1 |
-------------------------------
0 | 9.765 3.949
1 | 3.949 2.865
Y1=26.0157, u(Y1)=3.1249
Y2=12.5267, u(Y2)=1.6927404
rho(Y1,Y2)=0.746574
rho(Y2,Y1)=0.746574
po zakragleniu do 2 cyfr znaczacych:
Y1=26.02, u(Y1)=3.13
Y2=12.53, u(Y2)=1.70
