Entropia

 Cykl Carnota jest dobrym przykładem do wprowadzenia jeszcze jednej ważnej funkcji stanu. Zauważmy, że ze wzorów (13.3) i (13.8) wynika związek

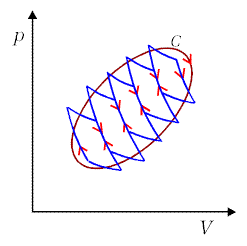
Związki te można łatwo uogólnić na dowolny cykl odwracalny traktując go jako złożenie wielu cykli Carnota, patrz Rys.13.3. Wówczas dla każdego elementarnego cyklu mamy

Stosunek ilości ciepła pobranego z danego źródła do jego temperatury bezwzględnej nazywamy ciepłem zredukowanym. Widzimy więc, że suma ciepeł zredukowanych w każdym elementarnym cyklu Carnota równa jest zeru. 

	Kiedy zapiszemy takie równania dla cykli, otrzymamy
		(13.14)
	Zwróćmy uwagę, że adiabaty znajdujące się wewnątrz konturu przekrywają się parami, co odpowiada sprężaniu i rozprężaniu gazu. W rezultacie następuje kompensacja pochodzących od nich wkładów i sumaryczny cykl zawiera tylko elementy brzegowe izoterm i adiabat. W ten sposób przybliżamy dowolny odwracalny cykl kołowy sumą cykli Carnota. Kiedy liczba cykli elementarnych rośnie, otrzymujemy w granicy
Rys.13.3. Każdy proces odwracalny można aproksymować złożeniem cykli Carnota.		(13.15)

Widzimy, że całka po obwodzie zamkniętym z wyrażenia równa jest zeru. Oznacza to również, że w przypadku procesu przeprowadzającego układ ze stanu A do stanu B całka z tego wyrażenia nie będzie zależeć od drogi całkowania. (Przypomnij sobie analogiczną własność pracy wykonywanej w polu sił zachowawczych, omawianą w lekcji czwartej.) Własność ta oznacza, że funkcja określona tą całką jest funkcją stanu. Funkcję tą poznaliśmy już w lekcji dwunastej w interpretacji statystycznej jako wielkość związaną z prawdopodobieństwem stanu układu. Nosi ona nazwę entropii i oznaczana jest przez S.  Mamy więc: 

Dla kołowego procesu odwracalnego mamy

Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu A do stanu B 

 Podana tu definicja nie pozwala na wyznaczenie bezwzględnej wartości entropii bowiem z zależności (13.18), widać, że

Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma pryncypialne znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie. Ważną cechą entropii jest także jej addytywność, co oznacza, że entropia układu jest sumą entropii podukładów. Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej  mamy to wartość entropii jest dla tej przemiany stała; . Proces adiabatyczny nazywa się dlatego procesem izoentropowym.

Zauważmy, że w przypadku procesów nieodwracalnych wzrasta oddane otoczeniu ciepło o znaku ujemnym w stosunku do ciepła pobranego, któremu przypisaliśmy znak dodatni. Przyczyną jest niekwazistatyczny przebieg procesu, niedoskonała izolacja układu itp. 

Sprawność silników nieodwracalnych jest mniejsza niż odwracalnego silnika Carnota. Z nierówności (13.10) wynika, że

co możemy przepisać w postaci

Porównując tę zależność ze wzorem (13.12) widzimy, że ciepło zredukowane w procesach nieodwracalnych jest mniejsze niż w procesach odwracalnych Wartość całki z lewej strony wzoru (13.17) też będzie mniejsza w procesach nieodwracalnych niż w odwracalnych, dla których wartość ta równa jest zeru. Łącznie dla obu typów procesów możemy zapisać nierówność postaci

Nierówność ta zwana jest nierównością Clausiusa. Przypadek znaku równości dotyczy procesów odwracalnych.

Porównajmy ze sobą sumaryczne ciepło zredukowane i zmiany entropii dla przemian odwracalnych i nieodwracalnych. Rozpatrzmy cykl kołowy, w którym przemiana ze stanu A do B jest nieodwracalna, a przemiana z B do A jest odwracalna. W oparciu o nierówność Clausiusa możemy napisać 

gdzie wskaźnikami (n) i (o) oznaczyliśmy odpowiednio przemianę nieodwracalną i odwracalną. Dla przemiany odwracalnej mamy

Biorąc to pod uwagę możemy wzór (13.23) przepisać w postaci

lub inaczej

Oznacza to, że sumaryczne ciepło zredukowane w procesie nieodwracalnym jest mniejsze od zmiany entropii. Dla układu  izolowanego nie wymieniającego ciepła z otoczeniem  mamy , czyli

 Wzór (13.26) możemy dla takiego przypadku napisać w postaci

Rezultat ten znany jest jako prawo wzrostu entropii. Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.

Jeżeli w układzie zachodzą wyłącznie procesy odwracalne, albo układ osiągnął stan równowagi termodynamicznej wtedy entropia pozostaje stała. 

Jak wspominaliśmy już, stwierdzenie to stanowi zasadniczą wartość pojęcia entropii. Jest to funkcja stanu określająca kierunek przebiegu procesów, zarówno wyidealizowanych (odwracalnych) jak i rzeczywistych. Określając zmiany entropii możemy przewidzieć, czy dany proces jest  możliwy, czy też nie lub czy może zajść samorzutnie w układzie pozostawionym sobie.