Związek pomiędzy makroskopową i mikroskopową definicją entropii

Jeżeli korzystając z rozwiązania zadania 13.4 (a więc wychodząc z definicji entropii danej wzorem (13.16)) określisz zmianę entropii przy izotermicznym (T₁=T₂) rozprężaniu 1-go mola gazu doskonałego od objętości V₁ do V₂, oraz określisz logarytm stosunku prawdopodobieństwa stanu końcowego (N_A cząsteczek w objętości V₂) do prawdopodobieństwa stanu początkowego (N_A cząsteczek w objętości V₁) to przekonasz się, że otrzymasz te same wyrażenia, tj. 

W wyrażeniu po prawej stronie W₂=1 jest prawdopodobieństwem, że wszystkie cząsteczki są w objętości V₂, natomiast W₁ jest prawdopodobieństwem, że wszystkie cząsteczki  po rozprężeniu znajdą się w objętości V₁ . Wartość tę nietrudno określić zauważając, że pojedyncza cząsteczka będąc w objętości V₂ znajdzie się w obszarze o objętości V₁ z prawdopodobieństwem będącym stosunkiem V₁/V₂. Dla większej liczby cząsteczek prawdopodobieństwo to jest iloczynem prawdopodobieństw, bowiem zakładamy że położenia cząsteczek są od siebie niezależne. Dla wszystkich cząsteczek mamy więc 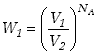. Stosunek tych prawdopodobieństw jest prawdopodobieństwem termodynamicznym czyli wagą statystyczną stanu o objętości V₂ w stosunku do stanu o objętości V₁. Pamiętając, że k=R/N_A  widzimy, po prostych przekształceniach algebraicznych, równoważność obu definicji entropii.