gdzie znak ładunku może być dodatni bądź ujemny. Kierunek siły zgodny jest z kierunkiem wektora natężenia pola, a zwrot zależny jest od znaku ładunku. 

Zapiszmy równania Newtona dla tego przypadku. Pamiętamy, że , gdzie jest masą cząstki, a    jest jej przyspieszeniem. Z kolei, przyspieszenie jest drugą pochodną wektora położenia i pierwszą pochodną wektora prędkości względem czasu. Wektory te mogą mieć dowolną orientację w przestrzeni.  Równanie ruchu ma więc postać. 

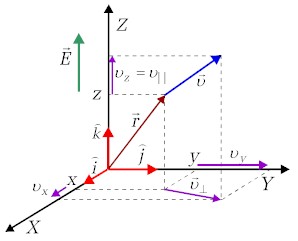
Określmy warunki początkowe dla naszego przypadku. Przyjmijmy, że wektor natężenia pola skierowany jest wzdłuż osi Z, czyli jego składowe można zapisać jako . Składowe wektora położenia i prędkości przyjmijmy za dowolne i oznaczmy je dla chwili czasu symbolami oraz. Ilustruje to rysunek 4.4.1.  Rys.2.5.1 Wektory: położenia, prędkości i pola elektrycznego

 Równania Newtona dla poszczególnych składowych oraz ich rozwiązania mają więc postać.

Zauważamy, że ruch w każdym z kierunków jest niezależny od ruchów w kierunkach pozostałych. Jeśli więc wszystkie prędkości początkowe równe będą zeru, to ruch będzie odbywał się tylko w kierunku zgodnym z kierunkiem wektora natężenia pola, czyli w naszym przypadku w kierunku osi Z. Będzie to ruch jednostajnie przyspieszony, jednowymiarowy.  Przyspieszenie w tym ruchu zapisać więc można w postaci skalarnej

bowiem kierunek przyspieszenia w tym ruchu jest także wielkością stałą.

Jeśli ładunek cząstki jest ujemny, to ruch będzie odbywał się w kierunku przeciwnym do kierunku wektora . Jeśli dodatkowo w chwili  składowa prędkości w kierunku Z była nierówna zeru i dodatnia to ruch będzie ruchem jednostajnie opóźnionym aż do momentu kiedy ujemny przyrost prędkości będzie równy prędkości początkowej, czyli kiedy .  Jeśli w chwili  składowa prędkości w kierunku X była nierówna zeru, to ruch w tym kierunku będzie ruchem jednostajnym, prostoliniowym, a cząstka poruszać się będzie w płaszczyźnie (X,Z) - będzie to więc ruch płaski. Zwróćmy tez uwagę, że przyspieszenie w tym ruchu określa czynnik wyrażający proporcjonalność przyspieszenia cząstki do wartości natężenia pola i ładunku cząstki i odwrotną proporcjonalność do jej masy.

Rozważania nasze możesz teraz sprawdzić samemu za pomocą przygotowanego w tym celu interaktywnego testu graficznego. 

Rozważmy bliżej ruch elektronu w polu elektrycznym. Ładunek elektronu wynosi (porównaj z tablicami stałych fizycznych) , a jego masa ; stosunek ładunku elektronu do jego masy wynosi . Natężenie pola wyrazić możemy w niutonach na kulomb lub, co jest ekwiwalentne,  w woltach na metr. Wymiar wyrażenia jest więc . W układzie SI wyrażenie to możemy więc zapisać dla elektronu w postaci

Wyraziliśmy to w metrach na nanosekundę do kwadratu, bo w praktycznych zastosowaniach wygodniej będzie wyrażać czas ruchu elektronu w nanosekundach.