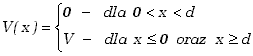
Rozwiązywanie równania Schrödingera nie należy na ogół do zadań łatwych, ale właśnie rozwiązania tego równania odzwierciedlają korpuskularno-falowe własności obiektów, które chcemy poznać. Własności te pojawiają się jako wynik nałożenia na funkcje stanowiące rozwiązania równania Schrödingera pewnych standardowych warunków: funkcje własne oraz ich pochodne muszą być jednoznaczne, skończone i ciągłe (poza niektórymi punktami osobliwymi). 

Rozważymy tu jeden z najprostszych przypadków, kiedy cząstka znajduje się w nieskończenie głębokiej studni potencjału.

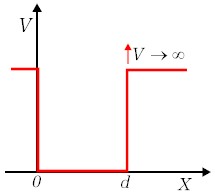
	Rysunek 12.4.1. przedstawia jednowymiarową studnię potencjału szerokości d i o głębokości V. Oznacza to, że energia potencjalna cząstki w funkcji położenia określona jest zależnością
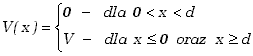		(12.4.1)
	My rozważać będziemy przypadek kiedy
Rys.12.4.1. Studnia potencjału
		(12.4.2)

Założenie to upraszcza nasze rozważania, bo poza obszarem gdzie prawdopodobieństwo znalezienia cząstki równe jest zeru, co oznacza, że 

(12.4.3)

W obszarze gdzie , czyli dla równanie Schrödingera (12.3.25) ma postać

(12.4.4)

Wprowadźmy pożyteczne oznaczenie

(12.4.5)

Równanie (12.4.4) przybiera teraz uproszczoną postać

(12.4.6)

Zauważmy, że jest to dokładnie taka sama postać jak równania (6.2a) w lekcji szóstej kursu Fizyka I, jeśli w równaniu tym wykonamy przyporządkowanie: . Rozwiązaniem tego równania są funkcje sinusoidalne ,  które można przedstawić w różnej postaci np. jako

(12.4.7)

Weźmy pod uwagę drugie z tych rozwiązań i nałóżmy na nie warunki naszego przykładu. Pamiętając, wzór (12.4.3), że otrzymujemy warunek

(12.4.8)

Wynika z tego natychmiast, że w naszym przypadku . Drugi warunek dotyczy zerowania się funkcji na drugiej krawędzi potencjału

(12.4.9)

z czego wynika, że

(12.4.10)

Biorąc pod uwagę związek (12.4.5) widzimy, że energia cząstki w studni potencjału może przyjmować tylko dyskretne wartości określone przez relację

(12.4.11)

Widać, że energia cząstki w nieskończenie głębokiej studni potencjału może przyjmować tylko dyskretne wartości określone wzorem (12.4.11). Wartości te zależne są od masy cząstki i kwadratu szerokości studni. Funkcje własne odpowiadające tym energiom otrzymamy wstawiając w argumencie funkcji sinus we wzorze (12.4.7) wyrażenie określające dozwolone w naszym przypadku wartości k. Otrzymujemy wtedy

(12.4.12)

Współczynnik A możemy wyznaczyć z warunku normalizacji (12.3.16) zastosowanego tu do przypadku jednowymiarowego. Otrzymujemy warunek

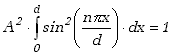(12.4.13)

Całkę tę można obliczyć różnymi sposobami. Najprościej jest zauważyć, że funkcja podcałkowa musi być równa zeru na krańcach przedziału całkowania oraz, że wartość średnia funkcjo podcałkowej będzie w takim przypadku równa 1/2. Całka równa więc będzie iloczynowi tej wartości średniej przez długość przedziału równą d, czyli d/2. Warunek (12.4.13) ma wiec postać

(12.4.14)

Funkcje własne dla naszego przypadku mają więc postać

(12.4.15)

W ten sposób rozwiązaliśmy równanie Schrödingera dla przypadku cząstki w nieskończenie głębokiej studni potencjału. Na zakończenie parę uwag, które pokażą potrzebę innego spojrzenia na fizykę mikroświata niż wynika to z "klasycznych" przyzwyczajeń.

1. Wartość n we wzorze (12.4.15) nie może przyjmować wartości zero - dlaczego? Gdyby tak było, to funkcja nie spełniałaby warunku unormowania, tzn. całka z niej nie byłaby równa jedności, bo byłaby równa zeru. Oznaczałoby to również, że zgodnie ze wzorem (12.4.11) określona jest dokładnie energia, a więc i pęd cząstki (są dokładnie równe zeru), czyli niepewność tych wartości też jest równa zeru. Położenie cząstki określone jest ze skończoną dokładnością równą d. Iloczyn niepewności byłby więc równy zeru, a przecież ma być nie mniejszy niż stała Plancka!
2. Wartości energii cząstki w studni potencjału nie mogą być dowolne, ale są skwantowane i dozwolone wartości określone są wzorem (12.4.11). Warunki tego typu nie istnieją w fizyce klasycznej. 
3. Kształt funkcji falowej dla różnych wartości d i n możesz zobaczyć korzystając z załączonej interaktywnej ilustracji graficznej. Możesz zobaczyć także rozkład gęstości prawdopodobieństwa znajdowania się cząstki w różnych miejscach studni dla różnych wartości n, czyli dla różnych poziomów energetycznych. Uruchamiając program w Excelu możesz zobaczyć, że prawdopodobieństwo znalezienia się cząstki ma charakter krzywej z wieloma maksimami, a ich liczba zależy od wartości n. Na rysunku poniżej, Rys. 12.4.2, pokazany jest przykładowy kształt funkcji falowej (krzywa koloru niebieskiego) oraz rozkład prawdopodobieństwa znajdowania się cząstki w różnych miejscach studni  (kolor czerwony) dla n=2. Widać, że w tym przypadku najmniej prawdopodobne jest znajdowanie się cząstki na brzegach i w środku studni. Nawet jednak dla n=1 prawdopodobieństwo to nie jest równomierne. Wręcz przeciwnie, dla bardzo dużych wartości n, prawdopodobieństwo to staje się jednakowe dla całego obszaru studni. Odpowiada to przewidywaniom fizyki klasycznej, gdzie żadne położenia nie są uprzywilejowane.   

A teraz sprawdź to sam -  korzystając z załączonej interaktywnej ilustracji graficznej. Zmieniaj wartości n, a czerwona krzywa pokaże Ci gdzie możesz spodziewać się znaleźć cząstkę. Zobacz, że dla n równego sto lub więcej prawdopodobieństwo to staje się równomierne. Fizyka kwantowa przechodzi w fizykę klasyczną. Nazywa to się zasadą korespondencji.