Gaz van der Waalsa

Własności gazów rzeczywistych bliskie są własnościom gazu doskonałego przy dostatecznie małych ciśnieniach i wystarczająco wysokich temperaturach. Jeśli warunki te nie są spełnione, to równanie stanu gazu doskonałego nie opisuje poprawnie własności gazów rzeczywistych.

Przy opisie mikroskopowych własności gazu doskonałego zakłada się, że cząsteczki gazu zajmują znikomą objętość, a ich oddziaływania sprowadzają się do zderzeń sprężystych. W rzeczywistości, objętość dostępna dla ruchu cząsteczek  jest pomniejszona, bowiem nie mogą one zbliżać się do siebie na odległość mniejszą niż wynosi średnica cząsteczki i nie mogą zbliżyć się do ścianek na odległość mniejszą od ich promienia. Ciśnienie także jest wynikiem nie tylko sprężystych i natychmiastowych zderzeń cząsteczek, ale również rezultatem ich wzajemnych oddziaływań. Objętość dostępna dla ruchu cząsteczek jest zatem pomniejszona w stosunku do objętości gazu doskonałego, a ciśnienie - powiększone.  Efekty te zostały uwzględnione w równaniu van der Waalsa w postaci dodatkowych członów, które dodaje się do ciśnienia i odejmuje od objętości..

Jeśli wartości i są równe zeru, otrzymujemy znane nam równanie stanu gazu doskonałego. Ciśnienie zwane jest ciśnieniem kohezyjnym. Ciśnienie to proporcjonalne jest do gęstości gazu i sił wzajemnego oddziaływania cząsteczek. Siły te także wzrastają proporcjonalnie do gęstości gazu, a gęstość jest odwrotnie proporcjonalna do objętości. Mamy więc

Zmniejszenie objętości proporcjonalne jest do liczby cząsteczek, a liczba ta, przy danym ciśnieniu, jest proporcjonalna do objętości naczynia. Objętość stanowi więc tę część objętości, która jest efektywnie zajęta przez cząsteczki gazu.

Wprowadzając oznaczenia: oraz , otrzymujemy równanie znane jako równanie van der Waalsa.

Stałe i charakteryzują własności danego gazu rzeczywistego.

Zależność ciśnienia od objętości przy stałej temperaturze dla gazu van der Waalsa wynikająca z równania (14.3) ma postać

Przykładowe izotermy van der Waalsa dla dwutlenku węgla CO₂ pokazane są na Rys. 14.1.

Z postaci wzorów (14.3)  i (14.4) oraz kształtu izoterm widzimy, że sprężając gaz przy stałej temperaturze mamy dla temperatur wysokich systematyczny wzrost ciśnienia przy zmniejszaniu się objętości, podobnie jak dla gazu doskonałego. Najmniejsza wartość objętości równa jest parametrowi , który opisuje efektywną objętość zajmowaną przez cząsteczki gazu. Kiedy więc objętość staje się bliska , to ciśnienie dąży do nieskończoności, bowiem różnica w mianowniku wyrażenia dąży do zera. Z kolei, wyrażenie obniża wartość ciśnienia, co przy stosunkowo niskich temperaturach powoduje powstanie lokalnego minimum w obszarze pomiędzy punktami C i B. 

Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury nie pojawia się minimum, ale jedynie punkt przegięcia na poziomym odcinku krzywej. Punkt ten zwany jest punktem krytycznym i na rysunku 14.1 oznaczony jest literą K. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę wartości krytycznych. Znaczenie tych wartości omówimy w dalszej części tego wykładu.

Znając wartości krytyczne dla danej substancji nietrudno jest wyznaczyć odpowiednie wartości współczynników a i b w równaniu van der Waalsa. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza  zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy zatem dla T=const

Z równań tych wyznaczamy

Współczynniki równania van der Waalsa wyrażone przez wartości krytyczne wynoszą

Tak wyznaczone współczynniki zostały użyte w naszej interaktywnej ilustracji izoterm van der Waalsa dla dwutlenku węgla, gdzie T_kr=304K,  p_kr=7.38MPa.

Na koniec warto zaznaczyć, że nasze dotychczasowe rozważania w tym wykładzieodnosiły się do jednego mola gazu. Kiedy rozważamy moli, wówczas dodatkowe człony równania (14.1) są: 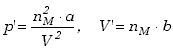 , a równanie van der Waalsa ma postać