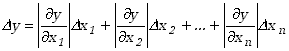
Pomiar jest podstawowym źródłem informacji w fizyce. Proces pomiaru polega na porównaniu wielkości mierzonego obiektu z wzorcem przyjętym za jednostkę. Wynik pomiaru zawiera zasadniczo dwie informacje: rodzaj jednostki (np. metr, sekunda, kilogram, amper itp.) oraz wartość liczbową, która określa ile razy mierzony obiekt jest większy lub mniejszy od przyjętego wzorca. 

Uzyskana w rezultacie wykonanego pomiaru wartość liczbowa nie jest jednak nigdy wyznaczona bezwzględnie precyzyjnie. Dlatego wynik pomiaru musi zawsze zawierać trzecią informację określającą jego dokładność. Bez tej informacji wynik pomiaru może prowadzić do zupełnie błędnych wniosków.

Dokładność pomiaru charakteryzujemy podając wartość tzw. niepewności pomiarowej zwanej też niekiedy błędem pomiaru. To drugie określenie, choć często używane, nie jest poprawne, bowiem pomiary właściwie wykonane nie powinny zawierać błędów, natomiast ich dokładność jest zawsze skończona.

Błędy i niepewności pomiarowe dzielimy na kilka rodzajów i w różny sposób uwzględniamy w analizie wyników pomiarów..

1. Błędy grube - powstające wskutek pomyłki wykonującego pomiar lub nagłej zmiany warunków pomiaru. Błędy grube należy eliminować, zaś wynik pomiaru nie powinien być obarczony ich wpływem.
2. Niepewności systematyczne - wynikające z niedoskonałości przyrządów pomiarowych lub metody pomiaru. Błędy tego typu należy (w miarę możliwości) korygować a ich granice powinny być wyraźnie określone.
3. Niepewności przypadkowe - występujące zawsze w pomiarach spowodowane są przez wiele różnorodnych czynników. Nie można ich ani wyeliminować ani skorygować. Należy jednak oszacować ich wartość i podawać jako jeden z elementów wyniku pomiaru.

Kiedy przy kilkakrotnym wykonywaniu pomiaru uzyskuje się ten sam wynik,  mamy do czynienia z przewagą niepewności systematycznych nad przypadkowymi, kiedy wyniki są różne, większy jest udział niepewności przypadkowych. Rzeczywiście, wykonując pomiar napięcia podręcznym woltomierzem wskazówkowym uzyskujemy na ogół wartość, która nie zmienia się jeśli powtórzymy pomiar. Gdybyśmy użyli precyzyjnego woltomierza cyfrowego okazałoby się, że ostatnia wskazana cyfra zmienia się nawet  w czasie trwania pomiaru. W pierwszym przypadku niepewności systematyczne woltomierza wskazówkowego były o wiele większe niż, występujące z pewnością również, niepewności przypadkowe. W drugim - woltomierz cyfrowy odnotowywał, nawet bardzo małe, przypadkowe zmiany napięcia. Rozpatrzmy pokrótce oba przypadki. Przyjmujemy założenie, że niepewności zastosowanego przyrządu oraz odczytu wartości mierzonej przez wykonującego pomiar nie kompensują się, ale sumują. Określoną w ten sposób niepewność pomiaru nazywamy niepewnością maksymalną. 

Kiedy mamy za zadanie wyznaczyć wielkość, która jest funkcją innych wielkości mierzonych, na przykład pole powierzchni walca na podstawie pomiaru jego średnicy i długości, musimy uwzględnić zależność funkcyjną wielkości wyznaczanej od wielkości mierzonych. Najczęściej stosujemy metodę różniczki zupełnej. 

Przyjmijmy, że chcemy ocenić niepewność wielkości  y, która jest funkcją mierzonych wielkości x₁, x₂,...x_n. (W naszym przykładzie mamy przyporządkowanie: y - pole powierzchni, x₁ - średnica, x₂ - długość mierzonego walca.) Korzystając z rozwinięcia funkcji y w szereg Taylora wokół wartości będącej wynikiem pomiaru, zaniedbując wyrazy wyższego rzędu i zastępując nieskończenie małe przyrosty zmiennych niezależnych wartościami przyrostów skończonych otrzymamy 

(1.1)

Zapis ten przypomina znane z matematyki pojęcie różniczki zupełnej. Wartości bezwzględne pochodnych cząstkowych wynikają właśnie z naszego założenia o sumowaniu się przyczynków niepewności. Skończone przyrosty  wartości  x,  to nasze niepewności  pomiarowe. Uzyskana w ten sposób wartość niepewności nosi nazwę niepewności maksymalnej.

W przypadku, kiedy nasza zależność funkcyjna ma postać iloczynowo/ilorazową możemy skorzystać z metody różniczki logarytmicznej. (Na przykład, z postacią taką mielibyśmy do czynienia przy wyznaczaniu objętości walca.)  Zapiszmy ogólnie taką funkcję dla dwóch zmiennych w postaci

(1.2)

gdzie a, n₁ oraz n₂ są wielkościami stałymi. Zlogarytmujmy obustronnie wyrażenie (1.2)

Zapisując teraz różniczkę logarytmu i traktując niepewności pomiarowe jako skończone przyrosty zmiennych niezależnych otrzymamy

Uzyskaliśmy w ten sposób nie wartość niepewności ale stosunek niepewności do samej wartości mierzonej. Stosunek ten , to niepewność względna, która jest wielkością bezwymiarową. 

Charakterystyczną cechą niepewności przypadkowych jest to, że na końcowy błąd pojedynczego pomiaru składa się suma wielu małych, niezależnych przyczynków, tzw. błędów elementarnych. W rezultacie, przy kilkakrotnym wykonywaniu pomiarów tej samej wielkości uzyskuje się różne wyniki. Wyniki te grupują się wokół wartości prawdziwej, zaś ich rozrzut może być miarą dokładności pomiaru. Samej wartości prawdziwej nie znamy, możemy jednak uzyskać wartość przybliżoną, oraz statystyczną ocenę jej dokładności. 

Gdybyśmy tych pomiarów wykonali bardzo wiele, okazałoby się, że ich rozkład ma formę podobną do dzwonu. Kształt tego rozkładu może być zapisany w postaci 

Jest to tzw. rozkład normalny lub rozkład Gaussa. Kształt tego rozkładu określony jest przez wartości dwóch parametrów: wartości przeciętnej oraz odchylenia standardowego . Pierwszy z nich określa położenie maksimum krzywej, drugi charakteryzuje "szerokość" rozkładu. W obszarze wokół wartości ograniczonym wartościami zawiera się ok. 68% wszystkich wartości x. Przykładowe kształty rozkładów Gaussa, uzyskane za pomocą programu EXCEL, przedstawione są poniżej.

Rozkład Gaussa jest rozkładem gęstości prawdopodobieństwa  f(x) dla zmiennej losowej, która może przyjmować dowolne wartości rzeczywiste. Oznacza to, że prawdopodobieństwo znalezienia wartości zmiennej losowej w przedziale pomiędzy liczbami  x₁  i  x₂ dane jest wyrażeniem

.

(1.6)

Kiedy wartość  x₁  we wzorze (1.6) zdąża do minus nieskończoności otrzymujemy wartość dystrybuanty rozkładu w punkcie x₂

.

(1.7)

Znając postać rozkładu dystrybuanty możemy łatwo obliczyć prawdopodobieństwo zadane całką we wzorze (1.6), bowiem

.

(1.8)

Kiedy  wartość  x₁  zdąża do minus nieskończoności, a wartość x₂ zdąża do plus nieskończoności otrzymujemy warunek unormowania rozkładu 

,

(1.9)

co oznacza, że prawdopodobieństwo zdarzenia pewnego równe jest jedności.

Rozkład normalny ma ogromne znaczenie w wielu działach nie tylko fizyki lecz ogólnie - nauki i techniki, dlatego warto poznać bliżej jego własności. Możesz uczynić to sam korzystając z załączonej poniżej interaktywnej ilustracji graficznej prezentującej zarówno postać rozkładu gęstości prawdopodobieństwa  jak i postać dystrybuanty rozkładu Gaussa dla wybranych przez Ciebie parametrów oraz . Przeczytaj podane tam objaśnienia i odpowiedz na załączone w arkuszu trzecim - pytania. 

MS-Excel	Interaktywna ilustracja graficzna	Kliknij w polu rysunku.
Rys.1.2. Rozkład normalny (Gaussa) dla a=0 oraz sigma=0.5.

Rozkład wyników pomiarów wokół wartości średniej jest właśnie praktycznym przykładem zastosowania rozkładu normalnego. Jeśli obliczymy wartość średnią z serii wykonanych pomiarów

(1.10)

a następnie obliczymy wartość wyrażenia

(1.11)

to uzyskamy przybliżoną wartość (estymator) drugiego z parametrów rozkładu normalnego, . Wartość ta charakteryzuje rozrzut wyników pomiarów wokół wartości średniej, którą możemy traktować jako estymator wartości przeciętnej w rozkładzie normalnym.. Ocenę niepewności samej wartości średniej możemy wyznaczyć z zależności

(1.12)

Zwróćmy uwagę, że tak wyznaczone oceny dokładności nie są niepewnościami maksymalnymi, bowiem, zgodnie z własnościami rozkładu normalnego tylko około 68% wyników pomiarów mieści w ich granicach.

Kiedy chcemy ocenić dokładność wyznaczenia wielkości będącej funkcją wyników pomiarów obarczonych niepewnościami przypadkowymi, korzystamy  ze wzoru  

(1.13)

Wzór ten zapisaliśmy dla dwóch zmiennych niezależnych: , ale w naturalny sposób można go uogólnić na większa liczbę zmiennych.

 Kiedy już wykonaliśmy pomiar i wyznaczyliśmy jego niepewność musimy prawidłowo zapisać jego wynik. Pamiętajmy, że wartości niepewności pomiarowych podajemy z dokładnością nie większą niż dwóch cyfr znaczących zaś samą zmierzoną wartość zaokrąglamy do tylu liczb znaczących ile wynika z zapisanej wartości niepewności. Typowym błędem studentów jest zapisywanie wyniku przepisując wszystkie cyfry znaczące z okienka kalkulatora czy ekranu komputera nie myśląc o tym, że pewna ich część nie niesie z sobą żadnej informacji fizycznej. Jest po prostu zbiorem liczb przypadkowych. 

Dla przykładu, jeśli wyznaczona wartość oraz jej niepewność wyniosły

,

to wynik ten zapiszemy jako

.

Na ogół przyjmuje się regułę, że wynik pomiaru zaokrąglamy "w dół", jeśli następna cyfra jest mniejsza niż  5,  w przeciwnym przypadku, zaokrąglamy "w górę". Wartość niepewności pomiarowej zaokrąglamy zawsze "w górę".

Ocena dokładności wykonanych pomiarów stanowi istotny fragment opracowania ćwiczeń laboratoryjnych z fizyki, wykonywanych przez studentów. W przypadku naszego kursu realizacja tego punktu programu studiów jest na razie niemożliwa. Tym bardziej więc należy zapamiętać podane tu podstawowe informacje.