Do tej pory intersowaliśmy się rozkładem jakiś np. liczby rejestracji cząstek, w zależności od czasu pamiaru. Rozkład zależał od czasu, bezpośrednio po przez czas pomiaru i pośrednio, po przez intensywność rejestracji cząstek (średniej liczby rejestracji na jednostkę czasu).
Możemy jednak rozpatrywać również zdarzenia związane z parametrami określającymi przestrzeń. W tej klasie zagadnień jest wiele takich, które podlegają rozkładowi Poissona. O to parę typowych przykładów.
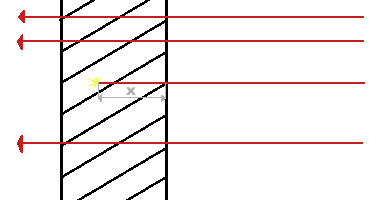
Wyobraźmy sobie, że oświetlamy target strumieniem cząstek, wywołujący w nim rozpady promieniotwórcze. Przy czym, przy przechodzeniu przez target strumień cząstek prawie nie zmienia swojej intensywności oraz jedna cząstka może wywołać tylko jeden rozpad (patrz poniższy rysunek).
Rysunek: Target bombordowany cząstkami.
(Za W. I. Goldański, A. W. Kucenko, M. I. Podgorecki; "Statystyka pomiarów przy rejestracji promieniowania jądrowego"; [1])
W takim przypadku wszystkie warunki rozkładu (patrz punkt 2) Poissona są spełnione z tym, że sens czasu ma teraz głębokość penetracji x. Rozkład rozczepień od głębokości ma postać
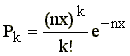 ,
,gdzie: n średnia ilość rozczepień na jednostkę długości.
Taki rozkład, zależny od x, nosi nazwę przestrzennego rozkładu Poissona.
Podobnym zagadnieniem jest zależność liczby jonizacji atomów grubej elmulsji, przez przelatujące przez nią szybką, ciężką cząstkę, od długości toru tej cząsteki. Na następującym rysunku widać zdjęcie napromieniowanej emulsji.

Rysunek: Ślady elektronów wybitych po przez szybką, ciężką cząstkę.
(Za W. I. Goldański, A. W. Kucenko, M. I. Podgorecki; "Statystyka pomiarów przy rejestracji promieniowania jądrowego"; [1])
Widać wzdłuż poszczególnych torów ślady oderwanych elektronów. Zakładamy przy tym, że jonizacja jakiegoś atomu nie zależy od tego czy inne atomy uległy jonizacji. I w tym przypadku rozkład liczby jonizacji od długości toru jest zgodny z rozkładem Poissona. Teraz przez x należy rozmieć długość toru, zaś n to średnia liczba jonizacji na jednostkę długość.
Można rozważać również przypadki wielowymiarowe . Niżej znajduje się zdjęcie emulsji, nasyconej przed wywołaniem substancją radioaktywną (tutaj roztwór soli toru).
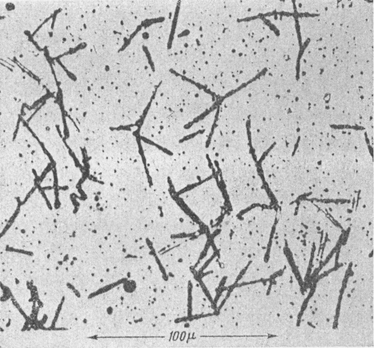
Rysunek: Ślady rozpadów jądrowych w grubej emulsji.
(Za W. I. Goldański, A. W. Kucenko, M. I. Podgorecki; "Statystyka pomiarów przy rejestracji promieniowania jądrowego"; [1])
Każdy rozpad promieniotwórczy uwidacznia się przez "gwiazdę" (grupa krótkich torów o wspólnym początku), utworzoną w wyniku przelotu produktów rozpadu.
Okazuje się, że rozkład liczby tych "gwiazd" na powierzchni emulsji, również podlega rozkładowi Poissona w postaci
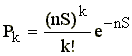
gdzie: S - interesująca nas powierzchnia, n - średnia liczba "gwiazd" na jednostkę powierzchni.
Analogiczny rozkład otrzymujemy dla zależności od objętości emulsji. Wystarczy zamienić S na V.