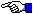2. Rozkład Poissona i kiedy mamy z nim doczynienia.

Rysunek: Schematyczny układ zliczający cząstki pochodzenia kosmicznego

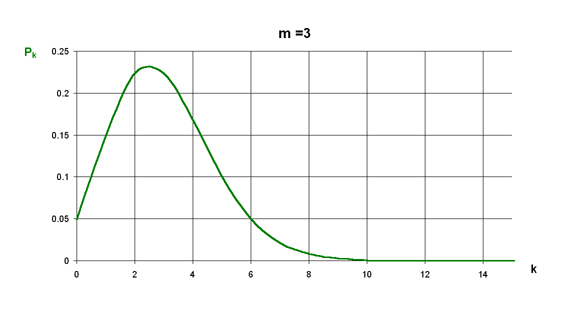
Zakładamy, że rejestracja jednej cząstki jest niezależna od rejestracji innej cząstki. Mamy do dyspozycji detektor rejestrujący te rozpady. Nasze pomiar polega na zliczaniu liczby zarejestrowanych cząstek przez pewien czas t. Oznaczmy tę liczbę przez k. Pomiar ten wykonujemy wielokrotnie (n - razy), notując za każdym razem otrzymane liczby rejestracji tzn. kolejne wartości k₁, k₂, k₃, k₂, ... k_n,.

Jeżeli przeprowadziliśmy naprawdę dużo tych pomiarów, to możemy się pokusić o wyznaczenie prawdopodobieństwa otrzymania konkretnej liczby k w jednym pomiarze.

Możemy założyć, że jest ono równe stosunkowi liczby pomiarów w których uzyskaliśmy k pomiarów do liczby wszystkich pomiarów (prawdziwe dla dużej liczby pomiarów).

gdzie: n_k liczba pomiarów w których wyszło k, n - liczba wszystkich pomiarów.

Okazuje się otrzymane prawdopodobieństwa zależą od k zgodnie ze wzorem:

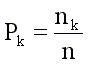
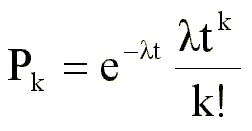
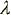gdzie: - pewien parametr, t - czas jednego pomiaru.

Wzór ten opisuje rozkład Poissona. A więc uzyskiwane liczby rejestracji, będące dyskretnymi zmiennymi losowymi podlegają właśnie temu rozkładowi.

Na poniższym rysunku widać jak wygląda graficzna reprezentacja przykładowego

Rysunek: Rozkład Poissona; t = 3.

(mimo że linie są ciągłe trzeba pamiętać że sens prawdopodobieństwa mają jedynie punkty dla całkowitych k)

Powstaje pytanie dlaczego właśnie rozkład Poissona, jeden z wielu rozkładów prawdopodobieństwa, tak dobrze opisuje otrzymywane przez nas wyniki. Odpowiedź tkwi w podstawowych założeniach rozkładu Poissona.

• Po pierwsze opisuje ono niezależne statystycznie zdarzenia - w naszym przypadku liczby zarejestrowanych cząstek nie zależą od siebie.
• Po drugie jest  to rozkład związany z dyskretnymi zmiennymi losowych - możemy otrzymać tylko tego typu liczby zarejestrowanych cząstek (nie można zarejestrować np. połowy cząstki).
• Po trzecie prawdopodobieństwa nastąpienia w bardzo krótkim przedziale czasu więcej niż jednego zdarzenia jest zerowe - w naszym przypadku zarejestrowanie w bardzo krótkim odcinku czasu więcej niż jednej cząstki jest znikome, praktycznie równe zero.
• I ostatni warunek: zmienne losowe mogą przyjmować jedynie nieujemne wartości - ten warunek jest również spełniony, nie możemy otrzymać ujemnej liczby cząstek.

Można pokazać, że wychodząc tylko z tych warunków można wyprowadzić postać rozkładu Poissona .

Spis treści