Wspominałem, że średnia m dla rozkładu Poissona zależy od dwóch parametrów - czasu
pomiaru t oraz intensywności promieniowania 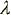 - zgodnie ze wzorem m =
- zgodnie ze wzorem m = 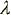 t.
t.
Na znajdującym się niżej obrazku widać zmiany kształtu rozkładu wraz ze wzrostem średniej.
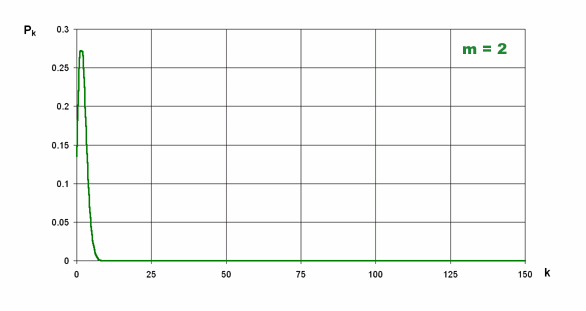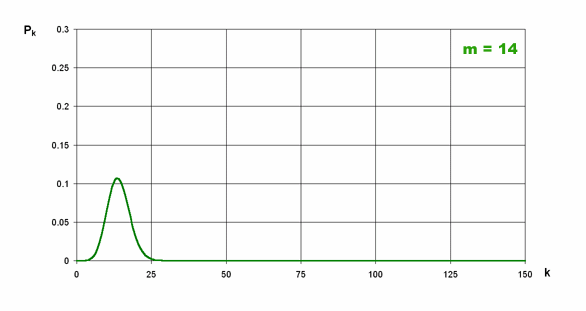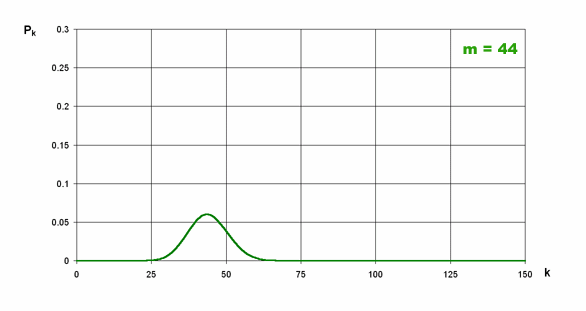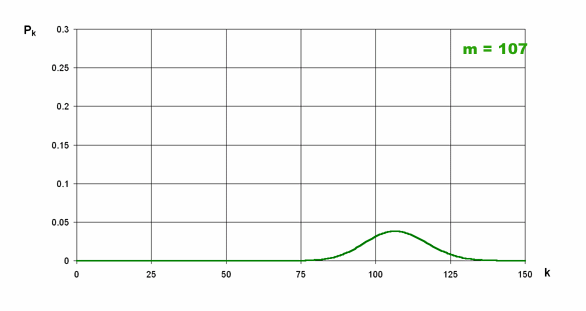
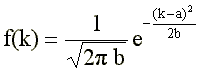
Poniższy przypadek pokazuje kształt obu rozkładów dla m = 75.
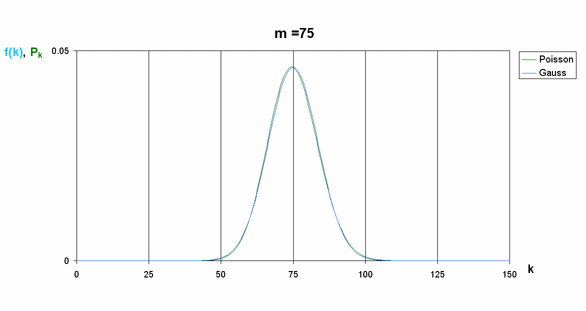
Rysunek: Rozkład Gaussa i Poissona dla m=75 (aby powiększyć kliknij)
J est to rozkładach prawdopodobieństwa dla zmiennych losowych typu ciągłego, podczas gdy my do tej pory zakładaliśmy, że k może być jedynie liczbą naturalną. Przejście do rozkładu ciągłego można jednak uzasadnić. Wielkość f(k)dk określa prawdopodobieństwo,że liczba cząstek jest w "nieskończenie małym" przedziale (k,k+dk) . Jeżeli interesuje nas przypadek w którym m jest bardzo duże (np. rzędu 1000) to dk liczące kilka jednostek w porównaniu z k, które bliskie m, możemy uważać za wielkość "nieskończenie małą".
Jak widać funkcja f(k) zależy od dwóch parametrów a i b, natomiast rozkład Poissona jest opisany jedynie przez średnią m. Można pokazać , że dla rozkładu Gaussa wielkość ta jest równa średniej, zaś parametr b wariancji. Ponieważ przejście między oboma rozkładami jest ciągłe to a = b = m i rozkład Gaussa ma postać.
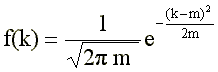
Jest jeszcze jeden problem, rozkład Gaussa opisuje zdarzenia losowe, które mogą przyjmować również wartości ujemne. Na szczęście funkcja f(k) bardzo szybko maleje wraz ze zwiększaniem się |k-m| i już nawet dla małych dodatnich k jest praktycznie równa zeru. Dla przykładu dla m = 50 otrzymujemy f(6)= 2.2*10-10 kiedy f(41)= 2.5*10-2 czyli ostatnia wartość jest około 10-7 raz większa.
Można pokazać że zarówno rozkład Poissona jak i rozkład Gaussa są unormowane ![]() .
.
Przy określaniu prawdopodobieństwa, że wielkość (k-m) jest w przedziale możemy wykorzystać fakt, że dla rozkłady Gaussa wielkość ta równa się:

Spis treści
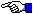
 to funkcja Gaussa
to funkcja Gaussa