Rozpatrzymy bardzo mały (w granicy nieskończenie mały)
przedział czasu dt oraz załóżmy, że prawdopodbieństwo ralizacji w
dt jednego zdarzenia P1(dt) jest proprcjonalne do dt, tzn
P1(dt) = ndt.
Ponadto szanse zrealizowania więcej niż jednego zdarzenia w dt są zerowe:
P1(dt) =P2(dt)=...=0.
Przyjmujemy, że wszystkie zdarzenia są statystycznie niezależne.
Zastanówmy się ile wynosi prawdopodobieństwo braku
zdarzenia w czasie t+dt. Oznacza to, że zarówno w przedziałach t jak
i dt nie nastąpiło żadne zdarzenia. Wykorzystujemy tutaj to, że zdarzenia
nie mogą się odejmowąć. Inaczej moglibyśmy dostać zero zdarzeń po czasie
t+dt mimo ich nastąpienia. Ze statystcznej niezależności między zdarzeniami
wspomniane prawdopodobieństwo wynosi
P0(t+dt)=P0(t)P0(dt)=P0(t)(1-ndt).
Zarazem jednak z rozwinięcia P0(t+dt) w szereg i obcięci na wyrach drugiego rzędu dostajemy.
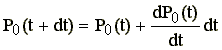 .
.
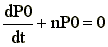 .
.
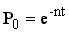 .
.
Szukamy teraz Pk(t) dla k większego 1.
Znowu wychodzimy od Pk(t+dt).
Takie zdarzenie zachodzi jeżeli w czasie t zaszło k, w dt żadne, lub w czasie
t - k-1 zdarzeń kiedy w dt jedno, lub w czasie t k-2 zdarzeń kiedy
w dt dwa, itd. aż do sytuacji, gdzie w czasie t - 0 zdarzeń w
dt - k.
Ze statystycznej niezależności
Pk(t+dt)=Pk(t)P0(dt)+Pk-1(t)P0(dt)+Pk-2(t)P1(dt)+...+.P0(t)Pk(dt).
Zaniedbując pk(dt) dla kwiększego od 1 dostajemy
Pk(t+dt)=Pk(t)P0(dt)+Pk-1(t)P1(dt).
Co jest równe
Pk(t+dt)=Pk(t)(1-ndt)+Pk-1(t)ndt.
Przy okazji również zachodzi
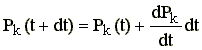 .
.
Z tych dwóch równań otrzymujemy układ równań.
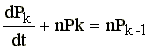 .
.
Rozwiązaniem tego układu jest właśnie równanie na Pk w postaci
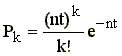 .
.
czyli właśnie równanie Poissona
Unormowanie rozkładów
Każdy rozkład prawdopodobieństwa musi spełnieć pewien warunek zwany unormowaniem.
Warunek ten oznacza, że suma (całka dla rozkładów ciągłych)
po wszystkich możliwych zdarzeniach musi być równa 1. Wynika
to z bezpośrednio z tego, że prawdopodbieństwo zdarzenia pewnego (a takim
jest suma po wszystkich zdarzeniach) musi być równa 1.
Dla rozkładu Poissona warunek ten jest spełniony. bo
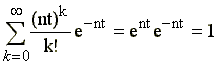 .
.
.
.
.
.
.
.
.
.
.
.