Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - dyfrakcji, czyli "uginania się" fal.

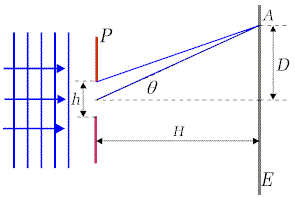
Zmodyfikujmy nieco rysunek 10.2.1. umożliwiając interferencję pomiędzy promieniami pochodzącymi z różnych punktów szczeliny. Dwa przykładowe promienie pokazane są na rysunku.   Szerokość szczeliny oznaczamy symbolem h. Podobnie jak poprzednio, zakładamy, że H>>h  i możemy uznać promienie biegnące z różnych punktów szczeliny za równoległe, co jest na ogół z niezłym przybliżeniem spełnione i upraszcza opis ilościowy. Taki przypadek nosi nazwę dyfrakcji Fraunhofera w odróżnieniu od dyfrakcji Fresnela, gdzie zakłada się,  że odległość pomiędzy źródłem i ekranem ma skończoną wartość.

Fig. 10.3.1. Dyfrakcja na pojedynczej szczelinie

Rozważmy na początek dwa promienie wybiegające z punktów szczeliny odległych o h/2. Warunek ich wygaszania się jest analogiczny do wzoru (10.2.2)

(10.3.1)

Na rysunku jeden promień jest na górnym krańcu szczeliny, drugi w jej środku. Możemy jednak przemieszczać się w dół z położeniami obu promieni odnajdując dla każdego promienia z górnej połowy szczeliny odpowiadający mu promień z połowy dolnej.

Możliwe są i inne kombinacje. Gdyby odległość pomiędzy rozważanymi promieniami była równa jednej czwartej szerokości szczeliny to warunek na wygaszanie byłby

(10.3.2)

Uogólniając można napisać, że warunek na wygaszanie się promieni biegnących z różnych punktów szczeliny ma postać

(10.3.3)

Minimów, i pomiędzy nimi maksimów, może więc być bardzo wiele. Powstaje więc pytanie jaki będzie rozkład natężeń w obrazie dyfrakcyjnym, jak natężenie wypadkowej fali zależeć będzie od kąta odchylenia promieni od pierwotnego kierunku? Największe wzmocnienie natężenia fali uzyskujemy, gdy obie fale mają taką sama fazę, największe osłabienie, gdy faza jest przeciwna. Pomiędzy tymi skrajnymi przypadkami mamy wszystkie przypadki pośrednie, zależne od różnicy faz.

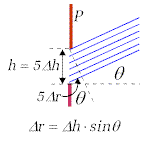Podzielmy w myśli całą szerokość szczeliny na n pasków. Ilustruje to pomocniczy rysunek obok, gdzie n=5. Różnica faz dla fal biegnących od dwóch sąsiednich pasków zależy od różnicy dróg , która związana jest z położeniem pasków względem siebie jak pokazano na rysunku..  Kiedy różnica dróg równa jest długości fali, to odpowiadająca różnica faz równa jest . Rys. 10.3.2. Przykładowy podział szczeliny na 5 pasków

  Mamy więc proporcję

(10.3.4)

gdzie jest odległością pomiędzy punktami w płaszczyźnie przesłony. 

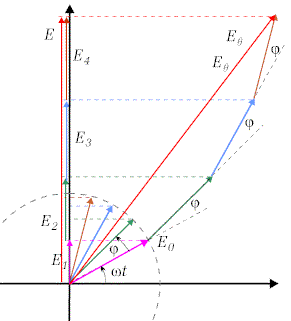Dla wyznaczenia sumarycznej różnicy faz oraz amplitudy wypadkowej fali  wykorzystamy tu metodę tzw. strzałek fazowych. Metoda ta umożliwia dodawanie wielkiej liczby fal o tej samej amplitudzie i częstości , a różniących się fazą. Ilustruje to rysunek 10.3.3. Niech amplituda pierwszej fali będzie wynosić , kolejna - różniąca się od pierwszej przesunięciem w fazie o będzie , kolejna niech będzie przesunięta o itd. (Na rysunku pokazane są przykładowo różnymi kolorami cztery fale i ich złożenie pokazane kolorem czerwonym.) Wypadkowa amplituda i faza może być otrzymana konstruując układ strzałek z których każda reprezentuje amplitudę i fazę i gdy kolejna ma swój początek w miejscu, gdzie kończy się poprzednia.

Rys. 10.3.3. Strzałki fazowe

 W naszym przypadku sumaryczna amplituda i sumaryczne przesuniecie fazowe będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem (10.3.4) od kąta określającego położenie danego punktu względem szczeliny. 

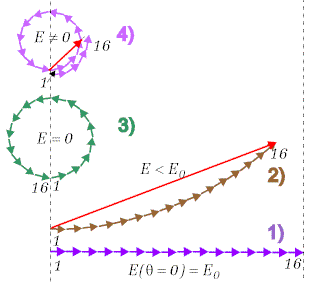Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą n jednakowych składników. Jeśli będzie inny, musimy sumować n przyczynków zgodnie z metodą strzałek fazowych. Ilustruje to Rys. 10.3.4, gdzie n=16. Przypadek 1) odpowiada sytuacji gdy . Sumaryczna amplituda jest tu maksymalna. Przypadek 2)  ilustruje sytuacje gdy jest różne od zera . Suma wszystkich 16 składników (długość łuku) jest taka sama, ale wypadkowa amplituda jest mniejsza. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta amplituda znów będzie różna od zera ale jej wartość stanie się o wiele mniejsza.

Rys. 10.3.4. Cztery przykłady konstrukcji amplitudy fali wypadkowej dla 16 strzałek fazowych i wzrastających wartości kąta .

 Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia . Związek pomiędzy wartością tego kąta, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na Rys. 10.3.4.

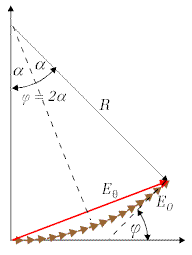	Kiedy liczba pasków będzie zmierzać do nieskończoności a ich szerokość do zera, to łuk strzałek fazowych  będzie można przybliżyć łukiem koła. Długość łuku jest  równa , a kąt pomiędzy stycznymi do łuku na obu jego końcach równy jest różnicy faz pomiędzy promieniami biegnącymi z obu krańców szczeliny. Kąt ten, mierzony w radianach,  równy jest z definicji stosunkowi długości łuku, czyli , do promienia R. tzn.  . Z kolei, jak widać na rysunku,  wypadkowa amplituda , zaś. Wynika z tego, że
	.	(10.3.5)
	Rys.10.3.5. Zależności geometryczne dla dyfrakcji na szczelinie.

 Wypadkowa różnica faz odpowiada promieniom biegnącym z dwóch krańców szczeliny i określona jest tak samo, wzór (10.3.4), jak różnica faz dla dwóch sąsiednich pasków, jeśli szerokość paska zamienimy szerokością szczeliny

(10.3.6

W ten sposób różnica faz określona została przez mierzalne wielkości: szerokość szczeliny, długość fali i kąt obserwacji. Podstawiając wyznaczoną wypadkową różnicę faz do  wzoru (10.3.5) otrzymujemy wyrażenie na amplitudę fali wypadkowej. Intensywność obrazu dyfrakcyjnego proporcjonalna jest do kwadratu amplitudy. Zapiszmy więc kompletny wzór na rozkład intensywności obrazu dyfrakcyjnego zależny jedynie od mierzalnych wielkości, czyli umożliwiający weryfikację doświadczalną. Przez oznaczamy względną intensywność określoną jako stosunek intensywności dla danego kąta do intensywności maksymalnej, czyli dla kąta równego zeru.

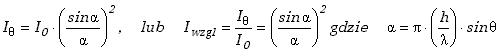(10.3.7)

Warto jest zobaczyć jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru (10.3.7) widać również, że zależy nie tyle od samych tych wartości, ale od ich stosunku. Jak kształt rozkładu intensywności wygląda w praktyce, możesz sprawdzić sam korzystając z zamieszczonej poniżej interaktywnej ilustracji graficznej.

Uzyskaliśmy interferencyjne efekty na pojedynczej szczelinie, zaś poprzednio rozważaliśmy układ dwóch szczelin, gdzie również określiliśmy warunki na wzmacnianie i wygaszanie wypadkowej fali interferencyjnej. Można się więc spodziewać, że w układzie dwóch szczelin, uzyskamy superpozycje obu dyskutowanych tu efektów. Pamiętamy, wzór (10.2.5), że w rezultacie nałożenia się dwóch fal o tych samych częstościach i amplitudach uzyskujemy fale wypadkową, której amplituda zależy od różnicy faz fal składowych. W naszym przypadku możemy amplitudę ze wzoru (10.2.5) zapisać następująco

(10.3.8)

gdzie przez E_i oznaczyliśmy amplitudę natężenia pola elektrycznego zależną od różnicy faz promieni przechodzących przez dwie szczeliny, a przez E_0i  amplitudę fali biegnącej z każdej szczeliny. Amplituda maksymalna E_m jest sumą obu amplitud składowych E_m=2E_0i . Podobnie jak i w przypadku dyfrakcji .  Należy jeszcze powiązać różnicę faz z kątem odchylenia promieni od pierwotnego kierunku fali padającej na układ szczelin. Wykorzystamy tu otrzymaną dla pojedynczej szczeliny zależność (10.3.6) gdzie zamiast szerokości szczeliny wstawiamy odległość pomiędzy dwoma szczelinami d.

(10.3.9)

Natężenie fali (intensywność) jest proporcjonalna do kwadratu amplitudy. Intensywność obrazu interferencyjnego możemy więc zapisać w postaci

(10.3.10)

gdzie jest maksymalną intensywnością  promieni biegnących z każdej szczeliny. Ta maksymalna intensywność zależna jest jednak od efektów dyfrakcyjnych i wyrażona jest wzorem (10.3.7). Intensywność łączna zawierająca w sobie oba efekty wyrazi się wiec wzorem (10.3.10) jeśli za podstawimy intensywność uwzględniającą efekty dyfrakcyjne ze wzoru (10.3.7). W rezultacie otrzymamy. 

(10.3.11)

Jest to końcowy wzór zależny wyłącznie od wielkości mierzalnych. Indeksami "i" i "d" oznaczyliśmy kąty odpowiadające interferencji i dyfrakcji. Symbolem d oznaczona jest odległość pomiędzy szczelinami, a symbolem h, szerokość każdej ze szczelin. I_m jest maksymalną intensywnością  odpowiadającą promieniom biegnącym na wprost.

Obraz interferencyjno - dyfrakcyjny określony wzorem (10.3.11) dla różnych kombinacji parametrów układu szczelin można zobaczyć korzystając z załączonej interaktywnej ilustracji graficznej.

Naturalnym rozszerzeniem układu dwóch szczelin jest układ wielu szczelin zwany siatką dyfrakcyjną, Rys. 10.3.8. 

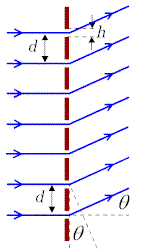Siatkę dyfrakcyjną charakteryzuje wielkość zwana stałą siatki d, która równa jest odległości pomiędzy dwoma sąsiednimi szczelinami, szerokość szczeliny a oraz liczba szczelin N; Rys.10.3.8. Oczekujemy, że w przypadku siatki dyfrakcyjnej efekt interferencyjny będzie silniejszy, bo sumować się będą składniki pochodzące od każdej pary sąsiednich szczelin. Wystąpią też efekty dodatkowe związane z interferencją pomiędzy innymi kombinacjami dwóch szczelin w siatce. Warunek wzmocnienia dla par sąsiednich szczelin będzie taki sam jak dla układu dwóch szczelin, czyli kąt odchylenia określony będzie stosunkiem długości fali padającej do stałej siatki, analogicznie jak we wzorze (10.2.1) Podobnie też jak w przypadku dwóch szczelin o określonych szerokościach wystąpią też efekty dyfrakcyjne zależne od szerokości samych szczelin h.  Rys.10.3.8. Schemat działania siatki dyfrakcyjnej

Zapiszemy więc warunek wzmocnienia w postaci

(10.3.12)

Wielkość n nazywamy rzędem widma. 

Dla znalezienia warunków określających położenia minimów postąpimy analogicznie do znajdowania minimów dyfrakcyjnych w pojedynczej szczelinie. Znajdziemy warunek wygaszania się  promieni z pierwszej i drugiej części siatki tj. odległych od siebie o Nd/2. Jeśli rozpatrujemy promienie odchylone względem pierwotnego kierunku o kąt , to ich różnica dróg  wynosić będzie (patrz Rys.10.3.2)

(10.3.13)

Pierwsze wygaszenie nastąpi kiedy ta różnica równa będzie połowie długości fali, czyli kiedy

(10.3.14)

Kolejne minima dane będą zależnością 

(10.3.15)

Kiedy jednak i stanie się równe N to zamiast minimum... spełniony zostanie warunek na pierwsze boczne maksimum, patrz wzór (10.3.12) dla n=1. 

Różnica kątowa pomiędzy maksimum głównym a najbliższym minimum charakteryzuje zdolność rozdzielczą siatki dyfrakcyjnej. Gdyby źródło emitowało dwie fale takie, że różnica ich długości byłaby równa , to uważamy, że możemy je rozróżnić jeśli maksimum dla jednej fali przypada na pierwsze minimum drugiej.  Położenie n-tego maksimum i pierwszego przy nim minimum dla fali o długości określają zależności

(10.3.16)

Maksimum drugiej fali o długości musi  być nie bliżej niż pierwsze minimum pierwszej fali, czyli musi być spełniony warunek

(10.3.17)

Wielkość R nazywamy zdolnością rozdzielczą siatki dyfrakcyjnej. Wniosek stąd, że dla uzyskania dużej zdolności rozdzielczej należy stosować siatki o wielkiej liczbie szczelin i analizować widma wysokiego rzędu.

A teraz sprawdź to sam -  korzystając z załączonej interaktywnej ilustracji graficznej.

 Efekty dyfrakcyjne możemy obserwować nie tylko dla światła widzialnego i dla fal przechodzących przez szczeliny. Ważną i wartościową z punktu widzenia badania struktur krystalicznych jest dyfrakcja odbiciowa wiązek promieni Roentgena na kryształach. Zjawisko dyfrakcji zachodzi na zbudowanej z atomów sieci krystalicznej i polega na nałożeniu się fal odbitych od płaszczyzn utworzonych przez atomy. Przykład dwuwymiarowy struktury sieci pokazuje rysunek 10.3.8. 

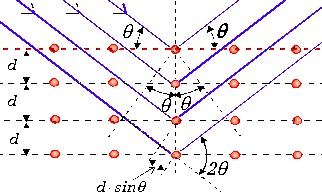Kolorem czerwonym zaznaczone są węzły sieci na których zachodzi zjawisko dyfrakcji. Odległość pomiędzy płaszczyznami poziomymi wynosi d. Kąt między płaszczyzną kryształu a promieniami padającymi równy jest . Padające na kolejne płaszczyzny fale płaskie ulegają odbiciu i jeśli różnica dróg optycznych fal odbitych od poszczególnych warstw równa jest całkowitej wielokrotności długości fali padającej, to wypadkowa fala odbita ma maksymalną amplitudę. Zależności geometryczne pomiędzy promieniami padającymi i odbitymi pokazane są na rysunku.

Rys. 10.3.8. Geometria dyfrakcji na kryształach.

 Warunek powstawania maksimów dyfrakcyjnych zwany jest prawem Bragga i wynika bezpośrednio z zależności geometrycznych  widocznych na rysunku 10.3.8. Aby po odbiciu uformowane zostało czoło zgodnych w fazie fal musi być spełniony warunek.

(10.3.18)

Prawo Bragga znajduje zastosowanie do badania struktury sieci krystalicznej, np. określania odległości miedzy płaszczyznowych. Z drugiej strony, umożliwia także analizę składu widmowego promieniowania Roentgena stanowiąc element metod spektroskopii rentgenowskiej. Stosując kryształy o znanych parametrach sieci krystalicznej można określić długość padającej fali, stosując promieniowanie o znanej długości można określić odległości pomiędzy płaszczyznami struktury krystalicznej.