Składniki Przyspieszenia

Jeszcze raz przypominamy zasadnicze założenie naszych rozważań. Przedział czasu, w którym obserwowane jest określone przesunięcie w dwóch różnych układach odniesienia jest taki sam, czyli .  Zakładamy więc, że czas upływa tak samo we wszystkich rozważanych tu układach odniesienia. W lekcji dziesiątej dowiemy się, że założenie to jest spełnione tylko dla prędkości znacznie mniejszych niż prędkość światła. 

Przyspieszenie jest pochodną prędkości względem czasu. Możemy to zapisać w  układzie nieruchomym wykorzystując wzory (7.3) i (7.4)  oraz znany z matematyki wzór na pochodną iloczynu;

Kolejna ważna uwaga!  Zapisaliśmy tu wyrażenie na przyspieszenie punktu materialnego w układzie nieruchomym poprzez pochodne (w układzie nieruchomym) wielkości wyrażonych w układzie poruszającym się, co symbolizuje znak ( ' ) przy wektorach prędkości i położenia. Związek pomiędzy pochodnymi dowolnego wektora w obu układach można zapisać w postaci (patrz objaśnienie).

Pamiętając definicję prędkości w układzie ruchomym (7.4) i założenie oraz wykonując zaznaczone w prawej części wyrażenia (7.8) działania, można przepisać wyrażenie to w postaci 

(7.9)

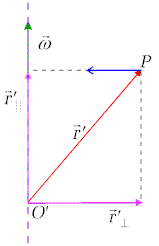Rys.4.2. Wektor położenia w układzie poruszającym się i jego składowe.

W końcowej części wyrażenia (7.9) mamy podwójny iloczyn wektorowy. Przypomnijmy znany z matematyki wzór pozwalający zapisać taki iloczyn trzech wektorów w bardziej użytecznej dla nas formie kombinacji iloczynów skalarnych.

(7.10)

W naszym przypadku w podwójnym  iloczynie wektorowym najpierw rozłożymy wektor położenia w układzie ruchomym na dwie składowe: równoległą i prostopadłą do chwilowej osi obrotu; patrz Rys. 4.2. Następnie skorzystamy z własności iloczynu wektorowego pamiętając, że iloczyn wektorowy dwóch wektorów równoległych wynosi zero. Wreszcie zastosujemy wzór (7.10) pamiętając z kolei, że iloczyn skalarny dwóch wektorów prostopadłych wynosi zero. W rezultacie otrzymamy.

(7.11)

Ostatecznie, więc wzór na przyspieszenie w układzie nieruchomym przybiera formę (7.12) gdzie: (7.13) Wzór (7.12) możemy też przedstawić w postaci (7.14) gdzie jest przyspieszeniem, które należy dodać do przyspieszenia ciała w układzie ruchomym, aby otrzymać jego przyspieszenie w układzie nie poruszającym się. Przyspieszenie to zawiera kilka składników.  (7.15)

Nazwijmy poszczególne składniki:

	przyspieszenie punktu w układzie poruszającym się,
	przyspieszenie będące rezultatem zmiany prędkości translacyjnej układu poruszającego się względem układu nieruchomego,
	przyspieszenia Coriolisa -Przyspieszenie, jakie ma ciało poruszające się w układzie obracającym się; nie występuje dla punktów spoczywających w układzie, który się obraca względem innego układu.
	przyspieszenie będące  rezultatem zmiany prędkości kątowej opisującej ruch wzajemny obu układów. Jeśli prędkość kątowa nie zmienia się, czyli przyspieszenie kątowe wynosi zero, to przyspieszenie to też jest równe zeru.
	przyspieszenie dośrodkowe - skierowane ku osi obrotu przyspieszenie ciała znajdującego się w układzie będącym w ruchu obrotowym

 Często mamy do czynienia z przypadkami, kiedy występują tylko niektóre ze składników we wzorze (7.15). Obecnie omówimy kilka najbardziej typowych przypadków.