From MJanik
Zadanie
Minimalizacja funkcji wielu zmiennych (5 pkt.)
Dana jest funkcja:
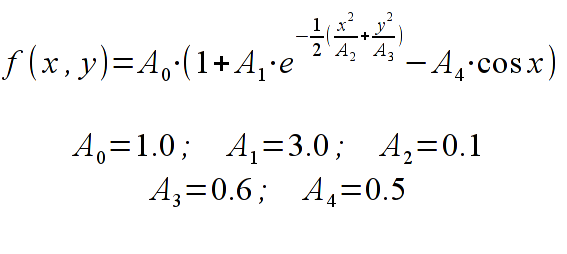
W zadaniu należy:
- Wygenerować (losowo -
GetRandom2) dane podlegające rozkładowi opisanemu powyższym wzorem. Należy uwzględnić szum pomiarowy, tzn. otrzymaną zmienną losową należy przeskalować przez liczbę losową (rozkład jednorodny) z przedziału 1.0-e .. 1.0+e, gdzie e=0.3.
- Dokonać minimalizacji funkcji celu określonej jako wartość statystyki chi-kwadrat, obliczonej dla funkcji teoretycznej (powyższy wzór) i wygenerowanych danych. W zadaniu należy wykorzystać obiekt klasy
TMinuit. Przykładowy skrypt znajduje się tutaj. Celem minimalizacji jest znalezienie parametrów A dla których dopasowanie jest najlepsze (wartość statystyki chi-kwadrat najmniejsza).
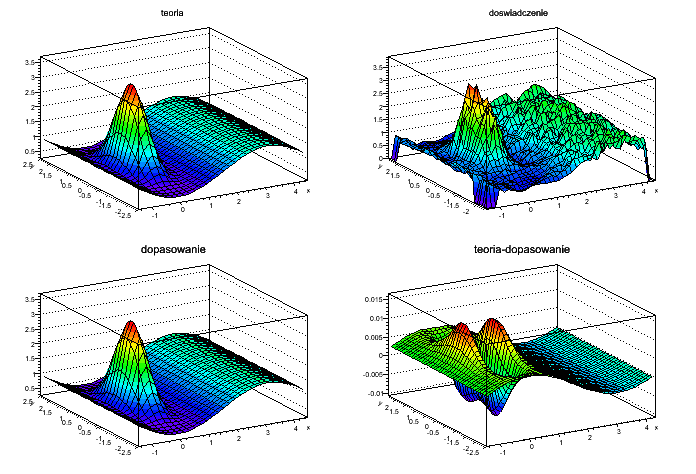
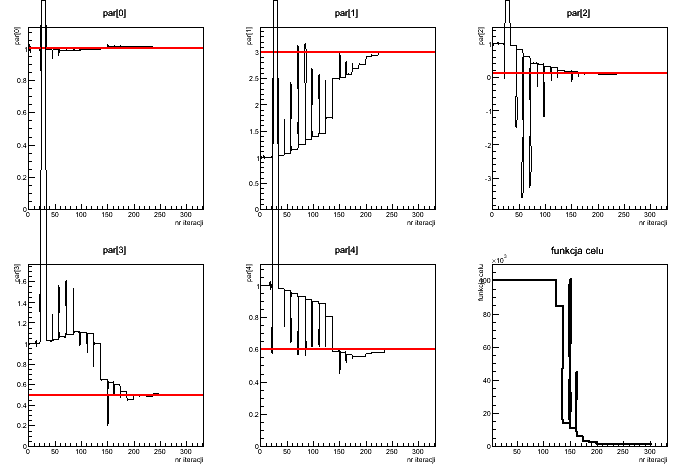
- Narysowć wykresy przedstawiające funkcję teoretyczną, wygenerowane dane, funkcję dopasowaną oraz różnicę między funkcją teoretyczną i funkcją dopasowaną. Ponadto, przedstawić wykresy zależności wartości parametrów oraz funkcji celu od numeru iteracji.
- Przeprowadzić test chi-kwadrat na poziomie istotności 0.01 w celu weryfikacji hipotezy o zgodności danych wygenerowanych (doświadczalnych) z dopasowaną funkcją.
- Przeanlizować dokładność i szybkość zbieżności procedury dopasowania w zależności od wyboru algorytmu minimalizcji (np. MIGRAD, SIMPLEX, MINIMIZE) oraz od początkowych wartości parametrów. Znaleźć największą wartość różnicy między teorią i dopasowaniem. Dla którego algorytmu jest ona najmniejsza? Proszę znaleźć przykłady parametrów początkowych, dla których minimalizacja jest nieskuteczna lub wolna oraz przykłady 'dobrych' parametrów.
Przykładowe wyniki