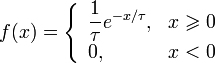From MJanik
(Difference between revisions)
|
|
| (5 intermediate revisions not shown) |
| Line 5: |
Line 5: |
| | == Zadanie == | | == Zadanie == |
| | | | |
| - | ''Część pierwsza:'' <b> liniowy kongruentny generator liczb losowych</b> | + | ''Część pierwsza'': '''liniowy kongruentny generator liczb losowych''' (1 pkt.) |
| | | | |
| | Należy napisać generator liczb pseudolosowych oraz zapisać wygenerowane liczby do pliku. | | Należy napisać generator liczb pseudolosowych oraz zapisać wygenerowane liczby do pliku. |
| Line 11: |
Line 11: |
| | Stworzony generator powinien opierać się na wzorze: | | Stworzony generator powinien opierać się na wzorze: |
| | | | |
| - | <code> | + | <code>x[j+1] = (g*x[j] + c) mod m.</code> |
| - | x[j+1] = ( a*x[j] + c ) mod m | + | |
| - | </code> | + | |
| | | | |
| - | Generator taki nazywamy generatorem LCG - czyli generatorem liniowym kongruentnym. Zadanie pewnej wartości poczatkowej x[0] definiuje nam zatem cały ciąg. Ponadto jest to ciąg okresowy. Okres zależy od doboru parametrów i przy spelnieniu kilku warunków osiąga maksymalnie wartość m. Warunki te to: | + | Generator taki nazywamy generatorem LCG - czyli generatorem liniowym kongruentnym. Zadanie pewnej wartości poczatkowej <code>x[0]</code> definiuje nam zatem cały ciąg, który ponadto jest ciągiem okresowym. Okres zależy od doboru parametrów i przy spelnieniu kilku warunków osiąga maksymalnie wartość <code>m</code>. Warunki te to: |
| - | * c i m nie maja wspolnych dzielników
| + | |
| - | * <code>b = a-1</code> jest wielokrotnoscia kazdej liczby pierwszej p, ktora jest dzielnikiem liczby m
| + | |
| - | * b jest wielokrotnością 4 jesli m tez jest wielokrotnością 4.
| + | |
| | | | |
| - | Dla uproszczenia należy przyjąć c = 0, otrzymując w ten sposób <b> multiplikatywny liniowy generator kongruentny (MLCG)</b>.
| + | * <code>c</code> i <code>m</code> nie maja wspolnych dzielników, |
| - | * Wartości a oraz m powinny być łatwe do modyfikacji w programie. | + | * <code>b = g-1</code> jest wielokrotnoscia kazdej liczby pierwszej <code>p</code>, ktora jest dzielnikiem liczby <code>m</code>, |
| | + | * <code>b</code> jest wielokrotnością 4 jesli <code>n</code> tez jest wielokrotnością 4. |
| | | | |
| - | Efektem działania makra powinien być plik nazwa.dat zawierający ciąg wygenerowanych liczb dla zadanych parametrów. Makro należy uruchomić trzy razy, otrzymując trzy pliki: losowe1.dat, losowe2.dat, losowe3.dat, dla parametrów odpowiednio:
| + | Dla uproszczenia należy przyjąć <code>c = 0</code>, otrzymując w ten sposób multiplikatywny liniowy generator kongruentny (MLCG). |
| - | * m=7 i a=3,
| + | |
| - | * m=97 i a=23,
| + | |
| - | * m=32363 i a=157.
| + | |
| | | | |
| | + | * Wartości <code>g</code> oraz <code>m</code> powinny być łatwe do modyfikacji w programie. |
| | | | |
| - | ''Część druga:'' <b> test widmowy</b>
| + | Efektem działania makra powinien być plik nazwa.dat zawierający ciąg wygenerowanych liczb dla zadanych parametrów. Makro należy uruchomić trzy razy, otrzymując trzy pliki: <code>losowe1.dat, losowe2.dat, losowe3.dat</code>, dla parametrów odpowiednio: |
| | | | |
| - | Należy przeprowadzić test widmowy aby przetestować jakość generatora. By to zrobić należy narysować na płaszczyźnie punkty o współrzędnych <code>(x[n], x[n+1])</code>. Uzyskany obraz utworzy wzór przypominający widmo generatora - stąd nazwa testu.
| + | * <code>m=97</code> i <code>g=23</code>, |
| | + | * <code>m=32363</code> i <code>g=157</code>, |
| | + | * <code>m=147483647</code> i <code>g=16807</code>. |
| | | | |
| - | Jeśli punkty będą rozłożone równomiernie generator można uznać za dobry. Jeśli zdecydowanie widać pewną okresowość - punkty powtarzają się wielokrotnie - generator nie działa poprawnie. Oczywiście na rozłożenie punktów wpływa jedynie dobór parametrów a i m.
| + | ''Część druga'': '''test widmowy''' (1 pkt.) |
| | | | |
| - | * Do tworzenia wykresów widma poleca się użycie obiektów <code>TH2D</code>
| + | Należy przeprowadzić test widmowy aby przetestować jakość generatora. By to zrobić należy narysować na płaszczyźnie punkty o współrzędnych <code>(x[n], x[n+1])</code>. Uzyskany obraz utworzy wzór przypominający widmo generatora - stąd nazwa testu. |
| | | | |
| - | Wynikiem działania programu powinny być trzy wykresy widma uzyskane na podstawie uprzednio zapisanych plików losowe1.dat, losowe2.dat, losowe3.dat.
| + | Jeśli punkty będą rozłożone równomiernie generator można uznać za dobry. Jeśli zdecydowanie widać pewną okresowość - punkty powtarzają się wielokrotnie - generator nie działa poprawnie. Oczywiście na rozłożenie punktów wpływa jedynie dobór parametrów <code>g</code> i <code>m</code>. |
| | | | |
| | + | * Do tworzenia wykresów widma poleca się użycie obiektów <code>TH2D</code>. |
| | | | |
| - | ''Część trzecia:'' <b>Generacja liczb losowych oparta na transformacji rozkładu jednorodnego</b>
| + | Wynikiem powinny być trzy wykresy widma. |
| | | | |
| - | Dowolna funkcja zmiennej losowej jest zmienną losową. Powstaje więc pytanie jaka jest gęstość zmiennej losowej Y jeżeli znana jest gęstość f(x). Zakładamy że prawdopodobieństwo g(y)dy jest równe f(x)dx gdzie dx odpowiada wartością dy. Warunek jest spełniony dla odpowiednio małych dx. Wynika stąd, że:
| + | ''Część trzecia'': '''generacja liczb losowych oparta na transformacji rozkładu jednorodnego''' (3 pkt.) |
| | | | |
| - | <code> g(y) = dy/dx f(x) </code> | + | Dowolna funkcja zmiennej losowej jest zmienną losową. Powstaje więc pytanie jaka jest gęstość zmiennej losowej Y jeżeli znana jest gęstość <code>f(x)</code>. Zakładamy że prawdopodobieństwo <code>g(y)dy</code> jest równe <code>f(x)dx</code> gdzie <code>dx</code> odpowiada wartością <code>dy</code>. Warunek jest spełniony dla odpowiednio małych <code>dx</code>. Wynika stąd, że: |
| | | | |
| - | Teraz jeżeli założymy, że gęstość prawdopodobieństwa f(x) = 1 dla <code> 0<=x<=1 </code> i f(x) = 0 dla x<= 0 i x>1 to powyższe równanie możemy zapisać w postaci:
| + | <code>g(y) = dx/dy f(x)</code> |
| | | | |
| - | <code> g(y)dy = dx = dG(y), </code> | + | Teraz jeżeli założymy, że gęstość prawdopodobieństwa <code>f(x)</code> wynosi 1 w <code>0<=x<=1</code> i <code>f(x) = 0</code> dla <code>x<= 0 i x>1</code> to powyższe równanie możemy zapisać w postaci: |
| | | | |
| - | gdzie G(y) jest dystrybuantą zmiennej losowej Y. Co po całkowaniu daje nam
| + | <code>g(y)dy = dx = dG(y),</code> |
| | | | |
| - | <code> x = G(y) => y = G-1(x). </code> | + | gdzie <code>G(y)</code> jest dystrybuantą zmiennej losowej <code>Y</code>. Co po całkowaniu daje nam |
| | | | |
| - | Jeśli zmienna losowa X ma rozkład jednostajny na odcinku pomiędzy 0 i 1 oraz jeśli znana jest funkcja odwrotna G-1(x) to funkcja g(y) opisuje gęstość prawdopodobieństwa rozkładu zmiennej losowej Y. | + | <code>x = G(y) => y = G^-1(x).</code> |
| | + | |
| | + | Jeśli zmienna losowa <code>X</code> ma rozkład jednostajny na odcinku pomiędzy 0 i 1 oraz jeśli znana jest funkcja odwrotna <code>G^-1(x)</code> to funkcja <code>g(y)</code> opisuje gęstość prawdopodobieństwa rozkładu zmiennej losowej Y. |
| | | | |
| | Używając tej metody należy wygenerować 10000 liczb z rozkładu: | | Używając tej metody należy wygenerować 10000 liczb z rozkładu: |
| | | | |
| - | [[File:lab06_wzor.png]] | + | [[File:Lab06_wzor.png]] |
| | + | |
| | + | Dla <code>tau = 2</code>: |
| | | | |
| - | Dla tau = 2:
| |
| | * Należy wygenerować 10000 liczb z rozkładu 0 do 1 używając generatora z części pierwszej. | | * Należy wygenerować 10000 liczb z rozkładu 0 do 1 używając generatora z części pierwszej. |
| - | * Analitycznie (na kartce) policzyć dystrybuantę tego rozkładu, a nastęþnie funkcję odwrotną. | + | * Analitycznie (na kartce) policzyć dystrybuantę tego rozkładu, a następnie funkcję odwrotną. (1 pkt.) |
| - | * Wygenerować rozkład f(x) - wrzucając wygenerowane wartości do histogramu - korzystając z: | + | * Wygenerować rozkład <code>f(x)</code> - wrzucając wygenerowane wartości do histogramu - korzystając z: (1 pkt.) |
| - | ** Liczb wygenerowanych z pliku. | + | ** liczb wygenerowanych wcześniej i wczytanych z plików <code>losowe1.dat, losowe2.dat, losowe3.dat</code>, |
| - | ** Standardowego generatora ROOT'a <code> gRandom->Rndm(1)</code>. | + | ** standardowego generatora ROOT'a <code>gRandom->Rndm(1)</code>. |
| - | * Narysować na jednym wykresie histogram (odpowiednio unormowany) oraz teoretyczną funkcję f(x) (obiekt <code> TF1</code>). | + | * Narysować na jednym wykresie histogram (odpowiednio unormowany) oraz funkcję teoretyczną <code>f(x)</code> (obiekt <code>TF1</code>). (1 pkt.) |
| | + | |
| | + | == Uwagi == |
| | + | * Wczytywanie danych z pliku: |
| | + | ifstream ifile; |
| | + | ifile.open("dane.dat"); |
| | + | double val; |
| | + | while(ifile>>val) |
| | + | { |
| | + | cout<<val<<endl; |
| | + | } |
| | + | ifile.close(); |
| | + | |
| | + | * Zapisywanie danych do pliku: |
| | + | ofstream ofile; |
| | + | ofile.open("dane.dat"); |
| | + | for(int i=0;i<N;i++) |
| | + | ofile<<val<<endl; |
| | + | } |
| | + | ofile.close(); |
| | + | |
| | + | == Wynik == |
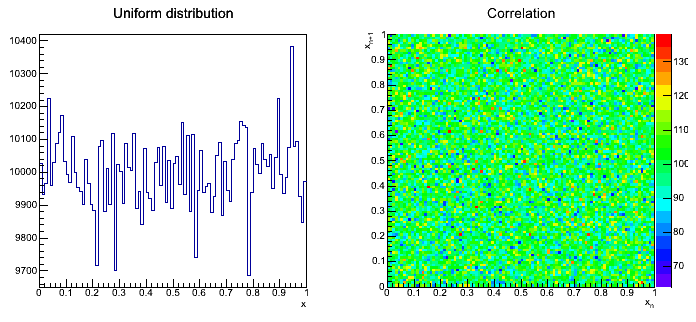
| | + | Przykładowy rozkład dla parametrów: |
| | + | * <code>m=97, g=23</code> |
| | + | [[File:lab06_n97_g23_2.png]] |
| | + | * <code>m=2147483647, g=16807</code> |
| | + | [[File:lab06_n2147483647_g16807_2.png]] |
| | + | |
| | + | Przykładowy wynik transformacji rozkładu jednorodnego: |
| | + | |
| | + | |
| | + | [[File:lab06_b_2.png]] |
Latest revision as of 08:15, 4 April 2012
Zadanie
Część pierwsza: liniowy kongruentny generator liczb losowych (1 pkt.)
Należy napisać generator liczb pseudolosowych oraz zapisać wygenerowane liczby do pliku.
Stworzony generator powinien opierać się na wzorze:
x[j+1] = (g*x[j] + c) mod m.
Generator taki nazywamy generatorem LCG - czyli generatorem liniowym kongruentnym. Zadanie pewnej wartości poczatkowej x[0] definiuje nam zatem cały ciąg, który ponadto jest ciągiem okresowym. Okres zależy od doboru parametrów i przy spelnieniu kilku warunków osiąga maksymalnie wartość m. Warunki te to:
-
c i m nie maja wspolnych dzielników,
-
b = g-1 jest wielokrotnoscia kazdej liczby pierwszej p, ktora jest dzielnikiem liczby m,
-
b jest wielokrotnością 4 jesli n tez jest wielokrotnością 4.
Dla uproszczenia należy przyjąć c = 0, otrzymując w ten sposób multiplikatywny liniowy generator kongruentny (MLCG).
- Wartości
g oraz m powinny być łatwe do modyfikacji w programie.
Efektem działania makra powinien być plik nazwa.dat zawierający ciąg wygenerowanych liczb dla zadanych parametrów. Makro należy uruchomić trzy razy, otrzymując trzy pliki: losowe1.dat, losowe2.dat, losowe3.dat, dla parametrów odpowiednio:
-
m=97 i g=23,
-
m=32363 i g=157,
-
m=147483647 i g=16807.
Część druga: test widmowy (1 pkt.)
Należy przeprowadzić test widmowy aby przetestować jakość generatora. By to zrobić należy narysować na płaszczyźnie punkty o współrzędnych (x[n], x[n+1]). Uzyskany obraz utworzy wzór przypominający widmo generatora - stąd nazwa testu.
Jeśli punkty będą rozłożone równomiernie generator można uznać za dobry. Jeśli zdecydowanie widać pewną okresowość - punkty powtarzają się wielokrotnie - generator nie działa poprawnie. Oczywiście na rozłożenie punktów wpływa jedynie dobór parametrów g i m.
- Do tworzenia wykresów widma poleca się użycie obiektów
TH2D.
Wynikiem powinny być trzy wykresy widma.
Część trzecia: generacja liczb losowych oparta na transformacji rozkładu jednorodnego (3 pkt.)
Dowolna funkcja zmiennej losowej jest zmienną losową. Powstaje więc pytanie jaka jest gęstość zmiennej losowej Y jeżeli znana jest gęstość f(x). Zakładamy że prawdopodobieństwo g(y)dy jest równe f(x)dx gdzie dx odpowiada wartością dy. Warunek jest spełniony dla odpowiednio małych dx. Wynika stąd, że:
g(y) = dx/dy f(x)
Teraz jeżeli założymy, że gęstość prawdopodobieństwa f(x) wynosi 1 w 0<=x<=1 i f(x) = 0 dla x<= 0 i x>1 to powyższe równanie możemy zapisać w postaci:
g(y)dy = dx = dG(y),
gdzie G(y) jest dystrybuantą zmiennej losowej Y. Co po całkowaniu daje nam
x = G(y) => y = G^-1(x).
Jeśli zmienna losowa X ma rozkład jednostajny na odcinku pomiędzy 0 i 1 oraz jeśli znana jest funkcja odwrotna G^-1(x) to funkcja g(y) opisuje gęstość prawdopodobieństwa rozkładu zmiennej losowej Y.
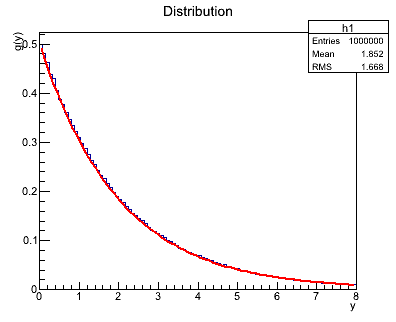
Używając tej metody należy wygenerować 10000 liczb z rozkładu:
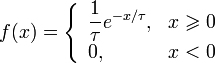
Dla tau = 2:
- Należy wygenerować 10000 liczb z rozkładu 0 do 1 używając generatora z części pierwszej.
- Analitycznie (na kartce) policzyć dystrybuantę tego rozkładu, a następnie funkcję odwrotną. (1 pkt.)
- Wygenerować rozkład
f(x) - wrzucając wygenerowane wartości do histogramu - korzystając z: (1 pkt.)
- liczb wygenerowanych wcześniej i wczytanych z plików
losowe1.dat, losowe2.dat, losowe3.dat,
- standardowego generatora ROOT'a
gRandom->Rndm(1).
- Narysować na jednym wykresie histogram (odpowiednio unormowany) oraz funkcję teoretyczną
f(x) (obiekt TF1). (1 pkt.)
Uwagi
- Wczytywanie danych z pliku:
ifstream ifile;
ifile.open("dane.dat");
double val;
while(ifile>>val)
{
cout<<val<<endl;
}
ifile.close();
- Zapisywanie danych do pliku:
ofstream ofile;
ofile.open("dane.dat");
for(int i=0;i<N;i++)
ofile<<val<<endl;
}
ofile.close();
Wynik
Przykładowy rozkład dla parametrów:
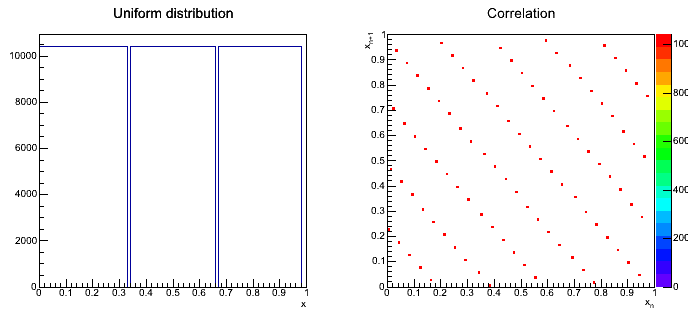
Przykładowy wynik transformacji rozkładu jednorodnego: