From Łukasz Graczykowski
(Difference between revisions)
|
|
| (One intermediate revision not shown) |
| Line 1: |
Line 1: |
| - | <!--
| |
| - |
| |
| | {| align="right" | | {| align="right" |
| | | __TOC__ | | | __TOC__ |
| Line 22: |
Line 20: |
| | | | |
| | == Uwagi == | | == Uwagi == |
| - | * Jako minimum i naksimum na osiach x oraz y we wszystkich obiektach ustawiamy 0 i liczbę PI | + | * Jako minimum i naksimum na osiach x oraz y we wszystkich obiektach ustawiamy 0 i liczbę PI/2 |
| | * Do pracy z histogramami należy wykorzystać obiekty <code>TH1D</code> i <code>TH2D</code>. Krótki przegląd możliwości tych obiektów można znaleźć w dokumencie: [ftp://root.cern.ch/root/doc/3Histograms.pdf Histograms] | | * Do pracy z histogramami należy wykorzystać obiekty <code>TH1D</code> i <code>TH2D</code>. Krótki przegląd możliwości tych obiektów można znaleźć w dokumencie: [ftp://root.cern.ch/root/doc/3Histograms.pdf Histograms] |
| | + | * Histogram gęstości prawdopodobieństwa tworzymy oprzez '''losowanie''' liczb pseudolosowych z funkcji gęstości (czyli musimy stworzyć obiekt TF2 jak na poprzednich zajeciach, następnie zrobić pętlę do założonej ilości losowań, pobrać dwie liczby funkcją '''GetRandom2''' oraz wypełnić funkcją '''Fill'' histogram gęstości) |
| | + | * Dystrybuantę liczymy '''numerycznie''' (dwie pętle '''for''' i całkujemy histogram gęstości iterujac po x oraz y, dla każdej iteracji poprzez '''SetBinContent''' ustawiamy wartości histogramu) |
| | + | * Gęstości brzegowe mają swoje funkcje w histogramach ('''podpowiedź:''' są to projekcje) |
| | + | * Do parametrów (średnie, odchylenia, kowariancje, współczynnik korelacji) - są odpowiednie metody |
| | | | |
| | == Przykładowy wynik == | | == Przykładowy wynik == |
| Line 40: |
Line 42: |
| | cov(X,Y)=-0.0137694 | | cov(X,Y)=-0.0137694 |
| | rho(X,Y)=-0.09661 | | rho(X,Y)=-0.09661 |
| - |
| |
| - | -->
| |
Latest revision as of 14:32, 16 March 2020
Zadanie
Dana jest gęstość prawdopodobieństwa:
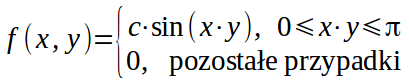
Należy:
- wyznaczyć stałą c w taki sposób aby rozkład gęstości był unormowany
- wylosować z rozkładu gęstości parę liczb (x,y) i następnie wypełnić nimi histogram gęstości prawdopodobieństwa f(x,y) (0.5pkt)
- unormować histogram gęstości prawdopodobieństwa (0.5pkt)
- wyznaczyć i narysować histogram dystrybuanty F(x,y) (1pkt)
- wyznaczyć i narysować histogram gęstości brzegowej g(x) i h(y) (1pkt)
- wyznaczyć:
- wartości oczekiwane: E(X), E(Y) (0.5pkt)
- odchylenia standardowe sigma(X), sigma(Y) (0.5pkt)
- kowariancję cov(X,Y) (0.5pkt)
- współczynnik korelacji rho(X,Y) (0.5pkt)
Uwagi
- Jako minimum i naksimum na osiach x oraz y we wszystkich obiektach ustawiamy 0 i liczbę PI/2
- Do pracy z histogramami należy wykorzystać obiekty
TH1D i TH2D. Krótki przegląd możliwości tych obiektów można znaleźć w dokumencie: Histograms
- Histogram gęstości prawdopodobieństwa tworzymy oprzez losowanie' liczb pseudolosowych z funkcji gęstości (czyli musimy stworzyć obiekt TF2 jak na poprzednich zajeciach, następnie zrobić pętlę do założonej ilości losowań, pobrać dwie liczby funkcją GetRandom2 oraz wypełnić funkcją Fill histogram gęstości)
- Dystrybuantę liczymy numerycznie (dwie pętle for i całkujemy histogram gęstości iterujac po x oraz y, dla każdej iteracji poprzez SetBinContent ustawiamy wartości histogramu)
- Gęstości brzegowe mają swoje funkcje w histogramach (podpowiedź: są to projekcje)
- Do parametrów (średnie, odchylenia, kowariancje, współczynnik korelacji) - są odpowiednie metody
Przykładowy wynik
Wykresy:
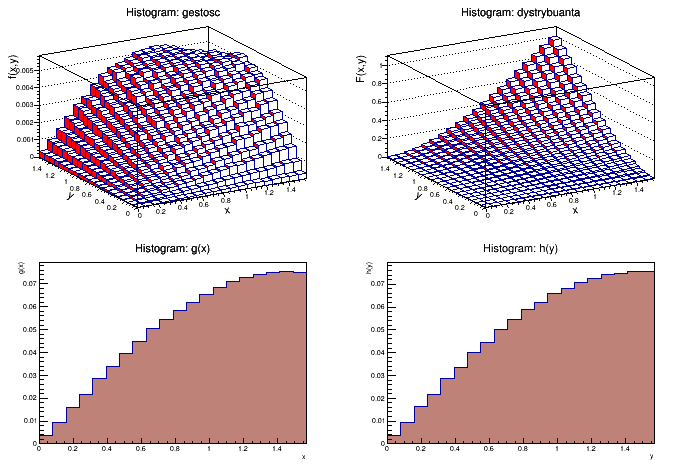
Wykres gęstości obrócony:
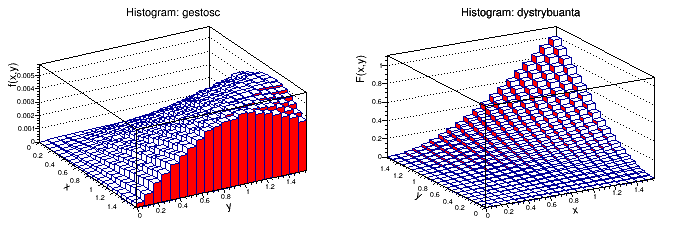
Output:
E(X)=0.990827
E(Y)=0.990535
sigma(X)=0.377467
sigma(Y)=0.377583
cov(X,Y)=-0.0137694
rho(X,Y)=-0.09661