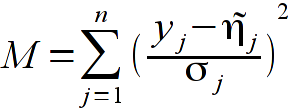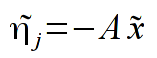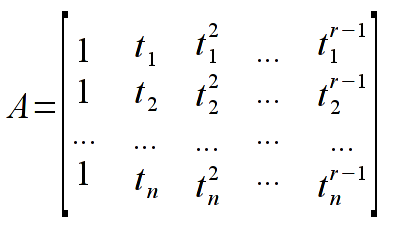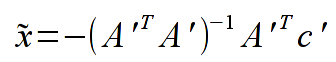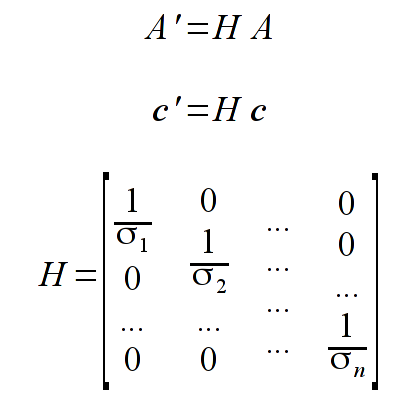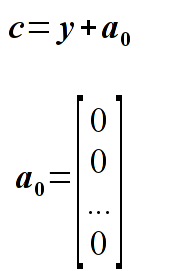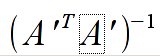From Łukasz Graczykowski
(Difference between revisions)
|
|
| Line 1: |
Line 1: |
| - |
| |
| | == Zadanie == | | == Zadanie == |
| - | '''Dopasowywanie danych przy użyciu ROOT'a''' (5 pkt.) | + | '''Metoda najmniejszych kwadratów''' (5 pkt.) |
| | + | |
| | + | Korzystając z metody najmniejszych kwadratów, dopasować do otrzymanych danych wielomiany stopnia <code>n=0..5</code>. |
| | + | |
| | + | * Proszę wczytać dane z [http://www.if.pw.edu.pl/~lgraczyk/KADD2016/lab11/dane.dat pliku]. Pochodzą one z eksperymentu zderzeń sprężystych ujemnie naładowanych mezonów K z protonami, przy ustalonej energii mezonu K. W pierwszej kolumnie znajdują się wartości cosinusa kąta rozpraszania w układzie środka masy, a w drugiej kolumnie odpowiadające im liczby zderzeń. Jako błędy pomiarów należy przyjąć pierwiastek kwadratowy z liczby obserwacji. Jeżeli otrzymany rozkład ma postać wielomianu, to wyznaczenie jego stopnia umożliwia wyznaczenie spinowych liczb kwantowych występujących stanów pośrednich ("Analiza danych", S.Brandt, Przykład 9.2.). |
| | + | |
| | + | * Proszę zaimplementować funkcję realizującą procedurę dopasowania metodą najmniejszych kwadratów. W tym celu należy wykorzystać wzory (ich wyprowadzenie znajduje się w [http://www.if.pw.edu.pl/~lgraczyk/KADD2018/Wyklad11-2018.pdf wykładzie 11] oraz w [http://www.if.pw.edu.pl/~majanik/files/wiel.ps instrukcji]): |
| | + | |
| | + | [[File:wzor1_new_asd.png]] |
| | + | |
| | + | [[File:wzor2.png]] |
| | + | |
| | + | [[File:wzor3.png]] |
| | + | |
| | + | [[File:wzor4.png]] |
| | + | |
| | + | [[File:wzor567.png]] |
| | + | |
| | + | [[File:wzor89.png]] |
| | + | |
| | + | ''Komentarz'': szukamy minimum funkcji M (odpowiednik statystyki chi-kwadrat), wartości <code>t_{j}</code> to cosinusy kąta rozproszenia (pierwsza kolumna pliku), wartości <code>y_{j}</code> to liczby obserwacji (druga kolumna). Estymatory <code>x</code> to poszukiwane współczynniki wielomianu. |
| | + | |
| | + | Przykładowy nagłówek funkcji: |
| | + | // Funkcja zwraca wartosc funkcji M |
| | + | // parametry: |
| | + | // st - stopien dopasowanego wielomianu |
| | + | // n - liczba pomiarow |
| | + | // tj - tablica cosinusow kata rozproszenia |
| | + | // yj - wyniki pomiarow |
| | + | // sigmaj - bledy pomiarow |
| | + | // wsp - tablica do ktorej nalezy wpisac wartosci wyznaczonych wspolczynnikow ([[File:wzor10.png]]) |
| | + | // bswp - tablica do ktorej nalezy wpisac bledy wyznaczonych wspolczynnikow (pierwiastki kwadratowe z elementów diagonalnych macierzy [[File:wzor11.png]]) |
| | + | double dopasuj (int st, int n, double *tj, double *yj, double *sigmaj, double *wsp, double *bwsp); |
| | + | |
| | + | Do zaimplementowania powyższych wzorów wygodnie jest skorzystać z klasy [http://www.slac.stanford.edu/comp/unix/package/cernroot/30106/TMatrixD.html TMatrixD]. Przykłady jej użycia: |
| | + | |
| | + | // utworzenie macierzy o wymiarach n x m |
| | + | TMatrixD *macierzA = new TMatrixD(n,m); |
| | + | |
| | + | // dostep do elementu o indeksach i,j macierzy macierzA, np.: |
| | + | (*macierzA)(i,j) = 1; |
| | + | |
| | + | // mnozenie macierzy: macierzA = macierzB macierzC |
| | + | TMatrixD *macierzA = new TMatrixD(*macierzB, TMatrix::kMult, *macierzC); |
| | + | |
| | + | // transponowanie macierzy |
| | + | TMatrixD *macierzAt = new TMatrixD(TMatrix::kTransposed,*macierzA); |
| | + | |
| | + | // odwracanie macierzy |
| | + | macierz->Invert(); |
| | + | |
| | + | * Proszę zinterpretować otrzymane dopasowania przeprowadzając test chi-kwadrat (korzystając z wyznaczonej wartości funkcji M). Należy określić stopień wielomianu, dla którego dopasowanie jest najlepsze oraz wyznaczyć najmniejszy stopień wielomianu, którego nie możemy odrzucić. Proszę wypisać wartości wyznaczonych współczynników wielomianu. |
| | + | |
| | + | == Wynik == |
| | + | |
| | + | [[File:mnk_2.png]] |
| | + | |
| | + | Output: |
| | + | |
| | + | Dopasowanie wielomianem stopnia 0 |
| | + | M = 833.548 |
| | + | x0 = 57.8452 +- 2.4051 |
| | + | Liczba stopni swobody=9 |
| | + | Kwantyl=21.666 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 0: odrzucamy |
| | + | |
| | + | Dopasowanie wielomianem stopnia 1 |
| | + | M = 585.449 |
| | + | x0 = 82.6551 +- 2.87498 |
| | + | x1 = 99.0998 +- 6.29159 |
| | + | Liczba stopni swobody=8 |
| | + | Kwantyl=20.0902 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 1: odrzucamy |
| | | | |
| - | Wczytujemy plik z danymi (histogram rozkładu masy inwariantnej): [http://www.if.pw.edu.pl/~lgraczyk/KADD2017/lab12/ExperimentalData.root plik]
| + | Dopasowanie wielomianem stopnia 2 |
| | + | M = 36.4096 |
| | + | x0 = 47.267 +- 3.24753 |
| | + | x1 = 185.955 +- 7.30235 |
| | + | x2 = 273.612 +- 11.6771 |
| | + | Liczba stopni swobody=7 |
| | + | Kwantyl=18.4753 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 2: odrzucamy |
| | | | |
| - | Chcemy otrzymać wynik dopasowania tła i sygnału:
| + | Dopasowanie wielomianem stopnia 3 |
| | + | M = 2.84989 |
| | + | x0 = 37.949 +- 3.62403 |
| | + | x1 = 126.546 +- 12.5894 |
| | + | x2 = 312.018 +- 13.4278 |
| | + | x3 = 137.585 +- 23.7499 |
| | + | Liczba stopni swobody=6 |
| | + | Kwantyl=16.8119 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 3: akceptujemy |
| | | | |
| - | [[File:Lab12_result.png|500px]]
| + | Dopasowanie wielomianem stopnia 4 |
| | + | M = 1.68602 |
| | + | x0 = 39.6179 +- 3.94036 |
| | + | x1 = 119.102 +- 14.3563 |
| | + | x2 = 276.49 +- 35.5643 |
| | + | x3 = 151.91 +- 27.2096 |
| | + | x4 = 52.5999 +- 48.7566 |
| | + | Liczba stopni swobody=5 |
| | + | Kwantyl=15.0863 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 4: akceptujemy |
| | | | |
| - | Całość dopasowujemy: tło - funkcja kwadratowa, sygnał - funkcja Lorentza
| + | Dopasowanie wielomianem stopnia 5 |
| | + | M = 1.66265 |
| | + | x0 = 39.8786 +- 4.29351 |
| | + | x1 = 121.384 +- 20.7054 |
| | + | x2 = 273.188 +- 41.6103 |
| | + | x3 = 136.571 +- 103.954 |
| | + | x4 = 56.8995 +- 56.2858 |
| | + | x5 = 16.7294 +- 109.424 |
| | + | Liczba stopni swobody=4 |
| | + | Kwantyl=13.2767 |
| | + | Poziom istotnosci=0.01 |
| | + | Stopien 5: akceptujemy |
Revision as of 11:54, 13 May 2019
Zadanie
Metoda najmniejszych kwadratów (5 pkt.)
Korzystając z metody najmniejszych kwadratów, dopasować do otrzymanych danych wielomiany stopnia n=0..5.
- Proszę wczytać dane z pliku. Pochodzą one z eksperymentu zderzeń sprężystych ujemnie naładowanych mezonów K z protonami, przy ustalonej energii mezonu K. W pierwszej kolumnie znajdują się wartości cosinusa kąta rozpraszania w układzie środka masy, a w drugiej kolumnie odpowiadające im liczby zderzeń. Jako błędy pomiarów należy przyjąć pierwiastek kwadratowy z liczby obserwacji. Jeżeli otrzymany rozkład ma postać wielomianu, to wyznaczenie jego stopnia umożliwia wyznaczenie spinowych liczb kwantowych występujących stanów pośrednich ("Analiza danych", S.Brandt, Przykład 9.2.).
- Proszę zaimplementować funkcję realizującą procedurę dopasowania metodą najmniejszych kwadratów. W tym celu należy wykorzystać wzory (ich wyprowadzenie znajduje się w wykładzie 11 oraz w instrukcji):
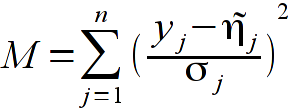
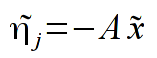
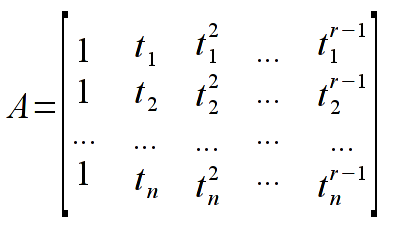
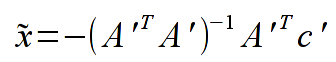
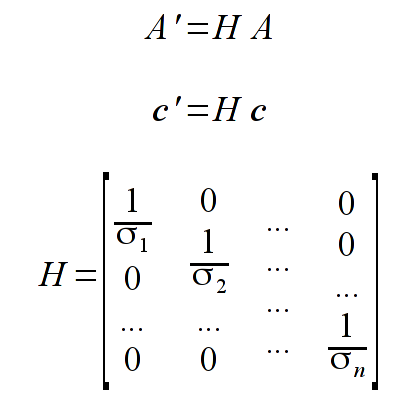
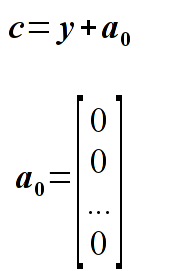
Komentarz: szukamy minimum funkcji M (odpowiednik statystyki chi-kwadrat), wartości t_{j} to cosinusy kąta rozproszenia (pierwsza kolumna pliku), wartości y_{j} to liczby obserwacji (druga kolumna). Estymatory x to poszukiwane współczynniki wielomianu.
Przykładowy nagłówek funkcji:
// Funkcja zwraca wartosc funkcji M
// parametry:
// st - stopien dopasowanego wielomianu
// n - liczba pomiarow
// tj - tablica cosinusow kata rozproszenia
// yj - wyniki pomiarow
// sigmaj - bledy pomiarow
// wsp - tablica do ktorej nalezy wpisac wartosci wyznaczonych wspolczynnikow (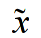 )
// bswp - tablica do ktorej nalezy wpisac bledy wyznaczonych wspolczynnikow (pierwiastki kwadratowe z elementów diagonalnych macierzy
)
// bswp - tablica do ktorej nalezy wpisac bledy wyznaczonych wspolczynnikow (pierwiastki kwadratowe z elementów diagonalnych macierzy 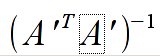 )
double dopasuj (int st, int n, double *tj, double *yj, double *sigmaj, double *wsp, double *bwsp);
)
double dopasuj (int st, int n, double *tj, double *yj, double *sigmaj, double *wsp, double *bwsp);
Do zaimplementowania powyższych wzorów wygodnie jest skorzystać z klasy TMatrixD. Przykłady jej użycia:
// utworzenie macierzy o wymiarach n x m
TMatrixD *macierzA = new TMatrixD(n,m);
// dostep do elementu o indeksach i,j macierzy macierzA, np.:
(*macierzA)(i,j) = 1;
// mnozenie macierzy: macierzA = macierzB macierzC
TMatrixD *macierzA = new TMatrixD(*macierzB, TMatrix::kMult, *macierzC);
// transponowanie macierzy
TMatrixD *macierzAt = new TMatrixD(TMatrix::kTransposed,*macierzA);
// odwracanie macierzy
macierz->Invert();
- Proszę zinterpretować otrzymane dopasowania przeprowadzając test chi-kwadrat (korzystając z wyznaczonej wartości funkcji M). Należy określić stopień wielomianu, dla którego dopasowanie jest najlepsze oraz wyznaczyć najmniejszy stopień wielomianu, którego nie możemy odrzucić. Proszę wypisać wartości wyznaczonych współczynników wielomianu.
Wynik
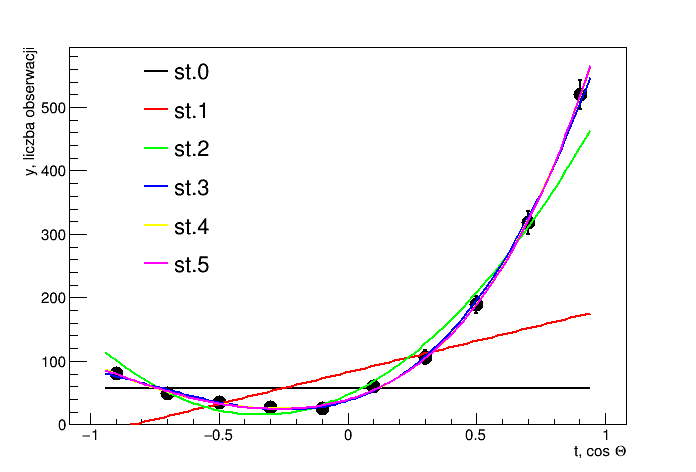
Output:
Dopasowanie wielomianem stopnia 0
M = 833.548
x0 = 57.8452 +- 2.4051
Liczba stopni swobody=9
Kwantyl=21.666
Poziom istotnosci=0.01
Stopien 0: odrzucamy
Dopasowanie wielomianem stopnia 1
M = 585.449
x0 = 82.6551 +- 2.87498
x1 = 99.0998 +- 6.29159
Liczba stopni swobody=8
Kwantyl=20.0902
Poziom istotnosci=0.01
Stopien 1: odrzucamy
Dopasowanie wielomianem stopnia 2
M = 36.4096
x0 = 47.267 +- 3.24753
x1 = 185.955 +- 7.30235
x2 = 273.612 +- 11.6771
Liczba stopni swobody=7
Kwantyl=18.4753
Poziom istotnosci=0.01
Stopien 2: odrzucamy
Dopasowanie wielomianem stopnia 3
M = 2.84989
x0 = 37.949 +- 3.62403
x1 = 126.546 +- 12.5894
x2 = 312.018 +- 13.4278
x3 = 137.585 +- 23.7499
Liczba stopni swobody=6
Kwantyl=16.8119
Poziom istotnosci=0.01
Stopien 3: akceptujemy
Dopasowanie wielomianem stopnia 4
M = 1.68602
x0 = 39.6179 +- 3.94036
x1 = 119.102 +- 14.3563
x2 = 276.49 +- 35.5643
x3 = 151.91 +- 27.2096
x4 = 52.5999 +- 48.7566
Liczba stopni swobody=5
Kwantyl=15.0863
Poziom istotnosci=0.01
Stopien 4: akceptujemy
Dopasowanie wielomianem stopnia 5
M = 1.66265
x0 = 39.8786 +- 4.29351
x1 = 121.384 +- 20.7054
x2 = 273.188 +- 41.6103
x3 = 136.571 +- 103.954
x4 = 56.8995 +- 56.2858
x5 = 16.7294 +- 109.424
Liczba stopni swobody=4
Kwantyl=13.2767
Poziom istotnosci=0.01
Stopien 5: akceptujemy