Statystyczna Eksploracja Danych

LABORATORIUM 8

MASZYNY WEKTORÓW NOŚNYCH

Maszyny wektorów nośnych (podpierających) [ang. support vector machines] są dość współczesną (z last 90-tych XX w.) metodą uczenia pod nadzorem. Ich podstawową cechą jest nowe spojrzenie na problem hiperpłaszczyzny rozdzielającej: zadanie polega na znalezieniu jak największego możliwego marginesu, rodzialającego punkty należące do różnych klas. Same hiperpłaszczyzny marginesów muszą przechodzić przez konkertne elementy próby uczącej i są nazwany właśnie wektorami podpierającymi. Problem został omówiony szerzej naWykładzie 6

Matematycznie oznacza to, że w przypadku próby uczącej o \(n\) obserwacjach mamy do czynienia z zagadnieniem funkcji Lagrange'a.

\(L(\mathbf{\alpha}) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y_i y_j \alpha_i \alpha_j (\mathbf{x}_i \cdot \mathbf{x}_j)\)

maksymalizowanej przy ograniczeniach

\(\begin{array}{ccc}\alpha_i \ge 0 & i = 1,...,n & \sum_{i=1}^n y_i \alpha_i = 0.\\\end{array}\)

W powyższych wzorach \(y_i=\{-1;1\}\) jest klasą wektora obserwacji \(\mathbf{x}_i\) natomiast \(\mathbf{x}_i \cdot \mathbf{x}_j\) jest iloczynem skalarnym. Współczynniki \(\alpha_i\) dają wartości niezerowe jedynie dla wektorów nośnych. Dzięki temu możliwe jest wyznaczenie wektora określającego hiperpłaszczyznę rozdzielającą

\(\mathbf{w} = \sum_{i=1}^n y_i \alpha_i \mathbf{x}_i\)

a wyraz wolny jest równy

\( b = \frac{1}{2} \left( \mathbf{w} \cdot \mathbf{x}^{*}_{1} + \mathbf{w} \cdot \mathbf{x}^{*}_{-1} \right) \)

gdzie \(\mathbf{x}^{*}_{1}\) i \(\mathbf{x}^{*}_{-1}\) to punkty, przez które przechodzą wektory nośne.

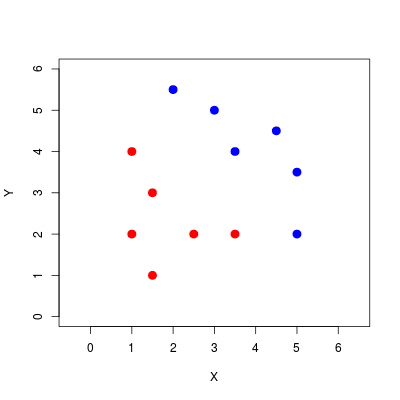
Jako ilustrację wykorzystamy prosty przykład z 12 obserwacjami z dwóch klas.

library(e1071)
# Dane
x <- c(1.0, 1.5, 1.0, 1.5, 2.5, 3.5, 2.0, 3.0, 3.5, 4.5, 5.0, 5.0)
y <- c(2.0, 1.0, 4.0, 3.0, 2.0, 2.0, 5.5, 5.0, 4.0, 4.5, 2.0, 3.5)

cl <- c(1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1)

data <- data.frame(x = x, y = y, class = as.factor(cl))

# Rysowanie danych
plot(data[,1:2], pch = 19, cex = 1.5, col = c("blue", "red")[data$class], xlim = c(0, 6), ylim = c(0, 6), xlab = "X", ylab = "Y", asp = 1)

Rysunek 9.1

Użyjemy funkcji svm() z biblioteki e1071, przy czym ponieważ funkcja jest dość ogólna i obsługuje różne przypadki, musimy podać dość konkretne opcje: wybrać klasyfikację, ustawić wysoki koszt, dać liniowe jądro, a także nie pozwolic na przeskalowywanie.

# Wywołanie metody SVM
data.svm <- svm(class ~ x + y, type = "C-classification", data = data, cost = 10, scale = F, kernel = "linear")

# Wektory nośne
print(data.svm$SV)

     x y.1
6  3.5 2.0
7  2.0 5.5
11 5.0 2.0
# Wartości współczynników alfa
print(data.svm$coefs) 
           [,1]
[1,]  1.5416840
[2,] -0.3264949
[3,] -1.2151892

Jak widać, jedynie trzy punkty stanowią SV (supporting vectors - wektory nośne), przy czym wartości współczynników \(\alpha\) kodują od razu klasę poprzez umieszczenie znaku - lub +..

Następnym krokiem jest wizualizacja działania algorytmu. W tym celu rozepniemy siatkę na współrzędnych i dokonamy przewidywania klas na tak skonstruowanych punktach za pomocą funkcji predict(), po czym wyniki wyświetlimy za pomocą funkcji image(), dodając oryginalne punkty.

# Rozpinanie siatki
xp <- seq(-1, 6, 0.01)
yp <- seq(-1, 6, 0.01)

gr <- expand.grid(x = xp, y = yp)

# Predykcja klas na siatce
M <- matrix(as.numeric(predict(data.svm, gr)), length(xp))

# Rysowanie obszarów przynależności do klas
image(xp, yp, M, col = c("lightgreen", "lightblue"), xlim = c(0, 6), ylim = c(0, 6), xlab = "X", ylab = "Y")

# Dodanie punktów
points(data[,1:2], pch = 19, cex = 1.5, col = c("blue", "red")[data$class])

Rysunek 9.2

Na koniec wyznaczymy wektor \(\mathbf{w}\) i dzięki niemu naniesiemy na wykres hiperpłaszczyznę rodzielająca oraz hiperpłaszczyzny marginesów.

# Wyznaczenie wektora w
w <- t(data.svm$SV) %*% data.svm$coefs
b <- data.svm$rho

xx <- 0:10

# Hiperpłaszczyzna rodzielająca
lines(xx, -w[1] / w[2] * xx + b / w[2], lty = 2, lwd = 2)

# Hiperpłaszczyzny marginesów
lines(xx, -w[1] / w[2] * xx + (b + 1) / w[2], lty = 2, lwd = 2, col = "red")
lines(xx, -w[1] / w[2] * xx + (b - 1) / w[2], lty = 2, lwd = 2, col = "blue")

Rysunek 9.3

BRAK SEPAROWALNOŚCI

Oczywiście, idealna separowalność klas jest pożądana, lecz nie zawsze możliwa do osiągnięcia. W takich wypadkach kluczową rolę odgrywa wartość \(C\), która określa "karę" za przekroczenie granicy marginesów. W zapisie matematycznym dalej dokonujemy maksymalizacji funkcji Lagrange'a

\(L(\mathbf{\alpha}) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y_i y_j \alpha_i \alpha_j (\mathbf{x}_i \cdot \mathbf{x}_j)\)

przy czym ograniczenie są teraz w postaci

\(\begin{array}{ccc}0 \le \alpha_i \le C & i = 1,...,n & \sum_{i=1}^n y_i \alpha_i = 0.\\\end{array}\)
library(MASS)

# Generowanie
draw.data.gauss <- function(S1, S2, m1, m2, n1, n2) {

X1 <- mvrnorm(n1, m1, S1)
X2 <- mvrnorm(n2, m2, S2)

X1 <- data.frame(X1); colnames(X1) <- c("x", "y")
X2 <- data.frame(X2); colnames(X2) <- c("x", "y")

X1$class <- 1; X2$class <- 2

data <- rbind(X1, X2); data$class <- factor(data$class)

return(data)
}

# Rysowanie punktów
plot.data <- function(data) {

cols <- c("blue", "red")

plot(data[,1:2], col = cols[data$class], cex = 2.5, pch = 19)
text(data[,1:2], labels = 1:nrow(data), cex = 0.8, col = "white", font = 2)

}

# Parametry danych z rozkładu Gaussa
S1 <- matrix(c(4, 2, 2, 4), 2, 2)
S2 <- matrix(c(4, 2, 2, 2), 2, 2)

m1 <- c(-1, -1)
m2 <- c(2, 2)

n1 <- 30
n2 <- 20

# Ustawienie ziarna dla losowania danych
set.seed(128)

# Generowanie obserwacji
data <- draw.data.gauss(S1, S2, m1, m2, n1, n2)

# Rysowanie danych
plot.data(data)

# Wywołanie metody SVM
data.svm <- svm(class ~ x + y, type = "C-classification", data = data, cost = 10, scale = F, kernel = "linear")

# Wypisywanie wektorów nośnych i wartości alfa
print(with(data.svm, cbind(SV, coefs)))

            x         y.1           
1   1.1887760 -1.12149780   5.125037
2   1.9523878 -2.28057082   3.667998
3   3.0173246  0.74834428  10.000000
5   2.1199128  0.06827946  10.000000
10  0.1188442  3.11589903  10.000000
12  0.1436874  0.94538990  10.000000
14 -0.4461424  1.54912322  10.000000
27  0.8645302  2.28290458  10.000000
30  2.1459450  2.50867866  10.000000
33 -0.2963546  0.70566865 -10.000000
34  1.1638198  2.98878072 -10.000000
35  0.2020300  1.52111496 -10.000000
36  3.1049032  0.34285937  -8.793036
39  1.0211324  2.90574104 -10.000000
40  1.5512155  0.78304568 -10.000000
45  1.4777660  2.22239838 -10.000000
47  1.5091429 -1.57514470 -10.000000
# Wyznaczenie wektora w w <- t(data.svm$SV) %*% data.svm$coefs
b <- data.svm$rho

xx <- -5:5
# Hiperpłaszczyzna rodzielająca
lines(xx, -w[1] / w[2] * xx + b / w[2], lty = 2, lwd = 2)

# Hiperpłaszczyzny marginesów
lines(xx, -w[1] / w[2] * xx + (b + 1) / w[2], lty = 2, lwd = 2, col = "blue")
lines(xx, -w[1] / w[2] * xx + (b - 1) / w[2], lty = 2, lwd = 2, col = "red")

Rysunek 9.4

Rzecz jasna, stałą \(C\) musimy dobrać sami, np. na podstawie próby testowej, kroswalidacji albo oceny prawdopodobieństwa błędnej klasyfikacji. Biorąc pod uwagę losowy charakter danych, zaproponowanie małej wartości \(C\) umożliwia przeciwdziałanie nadmiernemu dopasowaniu do próby uczącej. Poniżej wektory nośne oraz rysunek dla \(C=0.5\)

1   1.1887760 -1.12149780  0.50000000
2   1.9523878 -2.28057082  0.08643563
3   3.0173246  0.74834428  0.50000000
5   2.1199128  0.06827946  0.50000000
10  0.1188442  3.11589903  0.50000000
12  0.1436874  0.94538990  0.50000000
14 -0.4461424  1.54912322  0.50000000
18 -0.1897206  0.60902497  0.09466662
27  0.8645302  2.28290458  0.50000000
30  2.1459450  2.50867866  0.50000000
33 -0.2963546  0.70566865 -0.50000000
34  1.1638198  2.98878072 -0.50000000
35  0.2020300  1.52111496 -0.50000000
36  3.1049032  0.34285937 -0.50000000
38  2.3091887  2.07341323 -0.18110224
39  1.0211324  2.90574104 -0.50000000
40  1.5512155  0.78304568 -0.50000000
45  1.4777660  2.22239838 -0.50000000
47  1.5091429 -1.57514470 -0.50000000

Rysunek 9.5

JĄDRA NIELINIOWE

Zależność od przestrzeni obserwacji \(\mathbb{R}^p\) przejawia się jedynie przez obliczanie iloczynu skalarnego. Dlaczego jest to takie istotne? Otóż wszystkie takie obliczenia dotyczą jedynie iloczynu skalarnego, a nie przekształconych obserwacji, a dokonanie nieliniowej transformacji często umożlwia dokładną klasyfikację. W praktyce takie podejście sprowadza się do zamiany iloczynu skalarnego w funkcji Lagrange'a na opowiednie jądro \(K\)

\(L(\mathbf{\alpha}) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y_i y_j \alpha_i \alpha_j K(\mathbf{x}_i \cdot \mathbf{x}_j)\)
Co więcej, nie musimy de facto znać nawet nowej przestrzeni. Wystarczy, że jądro spełnia określone warunki, wynikające z tw. Mercera z analizy funkcjonalnej. Najczęściej stosowanymi jądrami są: wielomianowe, radialne i sigmoidalne, przy czym jądro radialne
\(K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma ||\mathbf{x}_i - \mathbf{x}_j||^2)\)

występuje wyjątkowo często.

Poniżej przykładowy zbiór danych.

# Jądro funkcji
K <- function(xi, xj, gamma) {
exp(-gamma*(sum((xi - xj)^2)))
}

# "Wnętrze" funkcji Lagrange'a
f <- function(xi, x, y, gamma) {

l <- length(xi$x)

sum(sapply(1:l, function(i) xi$alfa[i] * K(xi[i,c(1,2)], c(x,y), gamma)))
}

# Stała C oraz parametr gamma
C <- 100
gamma <- 0.5

set.seed(129)

# Generowanie rozkładu
data.radial <- data.frame(x = runif(20, -1.5, 1.5), y = runif(20, -1.5, 1.5))

data.radial$class <- with(data.radial, ifelse(sqrt(x^2+y^2) < 1, "klasa1", "klasa2"))
kolor <- ifelse(data.radial$class == "klasa1", "red", "blue")

data.radial.svm <- svm(class ~ x + y, type = "C-classification", data = data.radial, cost = C, gamma = gamma, scale = F)

data.radial$alfa <- 0
data.radial$alfa[data.radial.svm$index] <- data.radial.svm$coefs

# Punkty o współczynnikach |alfa| > 0
data.radial1 <- data.radial[abs(data.radial$alfa) > 0.001,]

# Rysowanie punktów
plot(data.radial[,1:2], col = kolor, cex = 2.5, pch = 19, xlim = c(-2,2), ylim = c(-2,2))
text(data.radial[,1:2], labels = 1:nrow(data.radial), cex = 0.8, col = "white", font = 2)

print(data.radial1)
             x             y  class       alfa
9   1.431222351 -9.802896e-02 klasa2   2.043324
11  0.770234668 -1.399431e+00 klasa2   0.674040
13  0.839799972  4.204576e-01 klasa1 -37.949851
15 -0.003407008  9.411202e-01 klasa1  -2.467940
16  0.633555739  9.585604e-01 klasa2   6.153747
17  1.030213225  5.635880e-01 klasa2  29.943637
19 -1.016943997  1.254212e-05 klasa2   1.603042

Rysunek 9.6

# Wyznaczanie współczynnika b
b <- data.radial.svm$rho

# Rozpinanie siatki
xp <- seq(-2, 2, 0.05)
yp <- seq(-2, 2, 0.05)

gr <- expand.grid(x = xp, y = yp)

# Predykcja klas na siatce
M <- sapply(1:nrow(gr), function(i) f(data.radial1, gr$x[i], gr$y[i], gamma))
M <- matrix(M, length(xp))
Mx <- matrix(as.numeric(predict(data.radial.svm, gr)), length(xp))

# Rysowanie obszarów przynależności do klas
image(xp, yp, Mx, col = c("lightgreen", "lightblue"))

# Hiperpłaszczyzna rodzielająca
contour(xp, yp, M, add = T, levels = b, lwd = 2, lty = 2, labels = "")

# Hiperpłaszczyzny marginesów contour(xp, yp, M, add = T, levels = b+1, lwd = 2, col = ifelse(b < 0, "blue", "red"), labels = "")
contour(xp, yp, M, add = T, levels = b-1, lwd = 2, col = ifelse(b < 0, "red", "blue"), labels = "")

# Dodanie punktów
points(data.radial[,1:2], col = kolor, cex = 2.5, pch = 19)
text(data.radial[,1:2], labels = 1:nrow(data.radial), cex = 0.8, col = "white", font = 2)

Rysunek 9.7

Zmiany parametrów mogą prowadzić do dziwnych efektów - poniżej \(C=1\) i \(\gamma=2\).

Rysunek 9.8