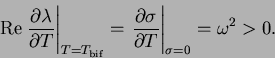| Lecture presented at the workshop "Complex Systems in Natural and Social Sciences" (CSNSS’99), 14-17 September 1999, Kazimierz Dolny, Poland |
Next: Bibliography
Up: Scientific cycle model with
Previous: Scientific cycle model with
We assume that changes in the time evolution of the system
-- natural sciences -- at time t depend on both
the state of the system at the current time, x(t), and
on the state in a certain past time ![]() .
The
feedback
.
The
feedback ![]() between present changes and past
states can be written as
between present changes and past
states can be written as
The system (1) constitutes the simplest model of
growth of natural sciences in which the rate of creation of
new results x(t) depends on the state of science (measured
by a number of scientific results) in the past ![]() .
.
In the real evolution there is many different ideas
having influence on the growth of science after delay time.
The delay ![]() can be interpreted as a notion of time to build,
connecting with time needed for deeper understanding of
theory content. Here the delay parameter
can be interpreted as a notion of time to build,
connecting with time needed for deeper understanding of
theory content. Here the delay parameter ![]() means the time needed for writing an essential paper, however
this parameter may have different interpretations.
Among physicists working on a given problem there is
a common feeling whether obtained result is important and
essential in the present status of science [1].
We assume that the speed of creation of new results in
time t is proportional to a number of results in time t-T.
We consider that increase of essential papers represents
the growth of science. These papers are necessary to write
a new essential paper because it builds up on older results.
Increase of knowledge given by a number of essential papers
in a unit of time is a function of a total number of papers
in different past moments Ti with some coefficients
means the time needed for writing an essential paper, however
this parameter may have different interpretations.
Among physicists working on a given problem there is
a common feeling whether obtained result is important and
essential in the present status of science [1].
We assume that the speed of creation of new results in
time t is proportional to a number of results in time t-T.
We consider that increase of essential papers represents
the growth of science. These papers are necessary to write
a new essential paper because it builds up on older results.
Increase of knowledge given by a number of essential papers
in a unit of time is a function of a total number of papers
in different past moments Ti with some coefficients ![]() .
.
Our model is the simplest in which there is included only
single constant delay parameter ![]() .
This toy model we can
explain observed periodicity in dynamics of growth sciences
[1,4,6].
There is a good evidence of exponential growth of
scientific results the initial developing of a new theory
[2,5].
.
This toy model we can
explain observed periodicity in dynamics of growth sciences
[1,4,6].
There is a good evidence of exponential growth of
scientific results the initial developing of a new theory
[2,5].
Following the de Sola Price model -- science is a dynamical
process with a positive feedback. New results in output are
given in input i.e.
This model can be enriched with both time delay and
the Miller mechanism of dying of some results
The delay in DDEs provides a natural method by which constant coefficient equations can be solved, even when these equations are nonlinear as in our example. However, this method requires tedious computations and often yields cumbersome solutions.
An analytically simpler method of describing solutions to DDEs ,
which is well known from the theory of ODE ,is the analysis of
the characteristic equation. In our case it is the equation
for linearized equation (3), i.e
After centering the fixed point at the origin (4) we
obtain x-x*=y, the linear equation for the perturbation
around a fixed point
| (5) |
We assume that there is a solution
![]() and
the characteristic equation for system (4) has the form
and
the characteristic equation for system (4) has the form
Our idea is to search for cyclic behaviour in the system (4). This behaviour is analogous to economic phenomenon known as business cycle. Therefore it can be described as scientific cycle.
The creation of cyclic behaviour is understood in terms of bifurcation theory. The Hopf bifurcation takes place if the pair of imaginary eigenvalues crossing transversally an imaginary axis on the Gauss plane. To prove this fact we can check that:
1) there is the pair of conjugated complex solution of (6)
in the form
![]() and there is only one
for which real part of eigenvalue
and there is only one
for which real part of eigenvalue
![]() ;
;
2) the transversality condition is fulfilled, i.e.
![]() .
.
After the decomposition the equation (6) on real and
imaginary part we obtain
Because of a reflection symmetry of this equation
![]() we can assume that
we can assume that ![]() .
The cyclic behaviour can appear if
.
The cyclic behaviour can appear if ![]() ,
and from
(7-8)
,
and from
(7-8)
This means that if
![]() there always exist
there always exist ![]() and consequently a periodic solution with the approximately
constant period
and consequently a periodic solution with the approximately
constant period
Now we must check the transversality condition
![\begin{eqnarray*}
{\rm Re} \frac{\partial \lambda}{\partial T} &=&
{\rm Re} \fr...
...- \lambda^2 - \lambda \beta] =
-(\sigma^2 - \omega^2) - \sigma
\end{eqnarray*}](img35.png)