RACHUNEK WARIACYJNY
Celem rachunku wariacyjnego jest
znajdowanie funkcji, które minimalizują funkcjonał (całkę w zagadnieniu
wariacyjnym).
Funkcjonałem nazywamy specjalny typ
funkcji, której wejściem jest funkcja, a wyjściem jest liczba rzeczywista.
Najczęściej spotykanym prostym funkcjonałem F[y(x)] jest
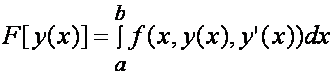
Funkcjonałem
jest F, a f – jest zwana funkcją
bazową - ponieważ dziedzina f nie musi należeć do zbioru liczb
rzeczywistych.
Równanie
Eulera-Lagrange’a:
Jeżeli y(x) jest funkcją,
która minimalizuje funkcjonał F[y(x)] w przedziale [a, b], to funkcja y(x)
spełnia następujące równanie różniczkowe (równanie Eulera-Lagrange’a):
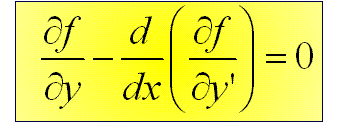
Tożsamość
Beltrami’ego:
Jeżeli funkcja bazowa f nie zależy w sposób jawny od x,
czyli gdy ∂f/∂x = 0, wtedy równaniu Eulera-Lagrange’a
odpowiada równoważne mu równanie
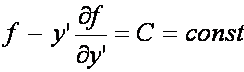
Funcjonał z wyższymi pochodnymi funkcji y(x): Dla funkcjonału
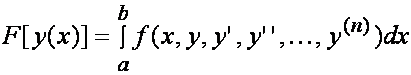
równanie
Eulera-Lagrange’a ma postać:
Funkcjonał z wieloma szukanymi funkcjami: Dla funkcjonału
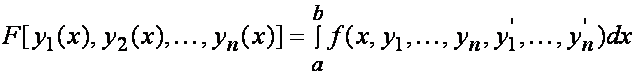
równanie
Eulera-Lagrange’a przechodzi w układ równań:
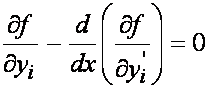
Funkcjonał z
kilkoma zmiennymi niezależnymi: Dla
funkcjonału
równanie
Eulera-Lagrange’a ma postać
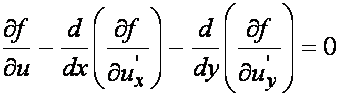
Przykład 1. Stosując
rachunek wariacyjny pokażemy, że na płaszczyźnie xy najkrótszą drogą między
punktami P(a, y(a)) i Q(b, y(b)) jest odcinek prostej. Długość łuku krzywej
y(x) przechodzącej przez P i Q wynosi
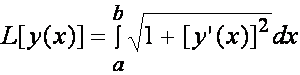
Tutaj 
, czyli 
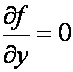. Zatem równanie
Eulera-Lagrange’a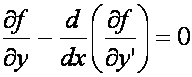 
sprowadza się do równania 
.
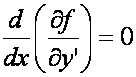Mamy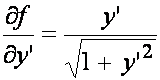 
oraz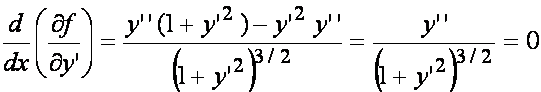 
.
Stąd,
równanie krzywej y(x) otrzymuje się z rozwiązania równania różniczkowego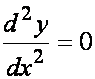 
. Po pierwszym całkowaniu
otrzymujemy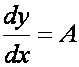 
, zaś po drugim 
. Jest to równanie prostej.
Stwierdziliśmy, że najkrótszą drogą
między punktami P i Q na płaszczyźnie jest odcinek prostej!
EUREKA!!!
LINIA
ŁAŃCUCHOWA – krzywa płaska
przypominająca swym kształtem zawieszony za swe końce łańcuch. W układzie
współrzędnych kartezjańskich równanie linii łańcuchowej ma postać
czyli
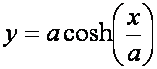
KATENOIDA
[łac. catena – łańcuch, gr. eidos – postać] – powierzchnia
utworzona przez obrót linii łańcuchowej dookoła osi y. Jest to jedyna
powierzchnia minimalna obrotowa. Jeśli umieścić dwa okręgi z drutu w
płaszczyznach równoległych, tak żeby prosta łącząca ich środki była prostopadła
do tych płaszczyzn, to błonka mydlana mająca te okręgi za brzegi, przyjmuje pod
wpływem sił napięcia powierzchniowego kształt katenoidy.
Przykład 2. Zagadnienie brachistochrony. Niech P i Q będą dwoma punktami na
płaszczyźnie pionowej i punkt P niech leży wyżej niż Q. Oba punkty łączymy
cienkim i giętkim drutem. Z punktu P puszczamy po drucie koralik, który
przesuwa się w dół bez tarcia tylko pod działaniem siły ciężkości Zagadnienie
brachistochrony polega na znalezieniu takiego kształtu drutu, jaki zapewni
najkrótszy czas spadku koralika.
Niech krzywa y(x) reprezentuje drut
łączący P i Q. Ustalimy współrzędne x-owe obu punktów jako a i b. Wtedy P = (a,
y(a)) oraz Q = (b, y(b)). Na podstawie zasady zachowania energii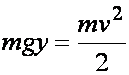 
znajdujemy prędkość 
. Czas spadku z punktu P do
Q wynosi
.
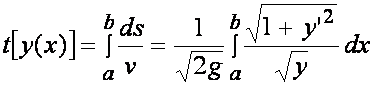Ponieważ
funkcja podcałkowa nie zależy w sposób jawny od x, to możemy wykorzystać
tożsamość Beltrami’ego i napisać
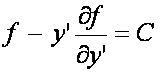czyli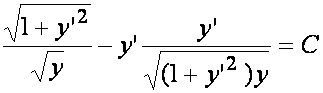 
albo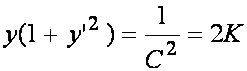 
.
Stosując
odpowiednią zamianę zmiennych otrzymujemy z tego równania różniczkowego
równanie parametryczne cykloidy.
Brachistochrona jest zatem odcinkiem
cykloidy. Interesującą jej własnością jest to, że koraliki dotrą do punktu końcowego Q w tym
samym czasie, niezależnie od ich położeń początkowych na cykloidzie.
Analiza stosunków energetycznych:
1. Określenie potencjałów
termodynamicznych. W warunkach równowagi przyjmują one najmniejszą możliwą
wartość. Jest to najmniejsza wartość funkcjonału.
2. Znalezienie wyrażeń na
składowe gęstości potencjałów, zwłaszcza gęstości energii swobodnej (funkcje
bazowe funkcjonału).
3. Ponieważ energia
swobodna jest całką z gęstości tej energii (wartością fukcjonału), to
poszukiwanie kształtu funkcji opisującej gęstość energii swobodnej przeprowadza
się za pomocą rachunku wariacyjnego, a nie zwykłego poszukiwania minimum
funkcji.
4. Konfiguracja
równowagowa może być znaleziona także w eksperymencie komputerowym (np. metodą
Monte Carlo).
5. W układach
dyssypatywnych nie ma konfiguracji równowagowej (ich istotą są stany
nierównowagowe, przepływy). Konfiguracja przepływów może być znaleziona
metodami zależnymi od konkretnego zagadnienia. Do układów dynamicznych stosuje
się także symulacje komputerowe metodami dynamiki molekularnej, metody siatkowe
itd.
SYMULACJE KOMPUTEROWE
METODA DYNAMIKI MOLEKULARNEJ
Jest to metoda deterministyczna
Metoda dynamiki molekularnej, jak sugeruje
jej nazwa, oblicza własności w oparciu o równania ruchu, co pozwala na
otrzymanie dla badanego układu tak własności statycznych, jak i dynamicznych. W
metodzie dynamiki molekularnej oprócz zwykłego równania Newtona
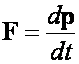
posługujemy się często równoważnymi równaniami Hamiltona
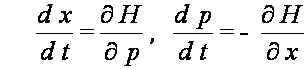
które mają tę zaletę, że
równanie Newtona II.go rzędu zastępują dwoma równaniami I.go rzędu. W tym
równaniu p oznacza pęd cząstki, a x i t są odpowiednio położeniami i czasem.
Funkcja H nosi nazwę hamiltonianu i jest sumą energii kinetycznej i
potencjalnej.
Np. dla oscylatora
harmonicznego
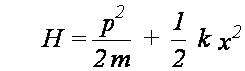
Stosujemy zasadę ergodyczności,
która zezwala na zamianę średnich po zespole przez średnie po czasie
METODA Monte Carlo
Jest to metoda stochastyczna
W metodzie Monte-Carlo otrzymuje się własności konfiguracyjne układu, chociaż i w przypadku tej metody istnieje interpretacja dynamiczna.
Podstawowy algorytm metody Monte Carlo:
1) Określ
punkt początkowy x0 w przestrzeni fazowej.
2)
Wygeneruj nowy stan x'.
3) Oblicz
prawdopodobieństwo przejścia W(x,x').
4)
Wygeneruj liczbę losową 
(rozkład równomierny).
5) Jeżeli
prawdopodobieństwo przejścia W jest mniejsze, niż liczba losowa R, wtedy
potraktuj stary stan jako nowy stan i wróć do kroku 2.
6) W
przeciwnym razie, zaakceptuj nowy stan i wróć do kroku 2.
Procedura
Metropolisa
