 |
|
|
 |
Sorry, it is still not translated :(
Programy tu zamieszczone udostępniane są w celach edukacyjnych.
Dołożyliśmy NAJWIĘKSZYCH starań, aby programy te działały prawidłowo
w zakresie technicznym a szczególnie merytorycznym.
Jednakże, ponieważ nie dysponujemy zespołem testerów, nie można wykluczyć,
że programy nie są wolne od błędów. Z tego powodu nie ponosimy żadnej odpowiedzialności
za jakiekolwiek szkody materialne i niematerialne mogące wyniknąć z użytkowania tych programów. |
 |
Rozmiar klastera perkolacyjnego
w funkcji średniego stopnia w klasycznych grafach przypadkowych
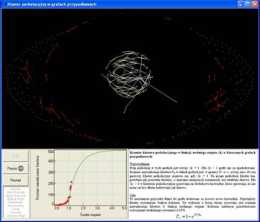 Próg perkolacji w tych grafach jest równy <k> = 1.
Dla <k> < 1 grafy nie są sperkolowane. Rozmiar największego klastera w takich grafach jest,
w granicy N dążącej do nieskończoności, równy zeru. Po raz pierwszy klaster perkolacyjny
pojawia się, gdy <k> = 1. Na progu perkolacji klaster ten, podobnie jak pozostałe klastery
o znacznie mniejszych rozmiarach, ma strukturę drzewa. Dla <k> > 1 w klasterze perkolacyjnym
pojawiają się dodatkowe krawędzie, które sprawiają, że nie może on być dłużej traktowany jak drzewo.
Program demonstruje wzrost klastera perkolacyjnego. Po nacisnięciu przycisku
Start do grafu dodawane są losowo nowe krawędzie. Największy klaster wyróżniono białym kolorem.
Na wykresie z lewej strony rysowany jest rozmiar największego klastera w funkcji średniego stopnia.
|
|
Wpływ preferencyjnego dodawania wierzchołków na wzrost sieci
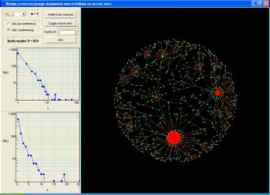
Potęgowy rozkład stopni wierzchołków w sieciach ewoluujących jest wynikiem dwóch,
wzajemnie uzupełniających się mechanizmów: wzrostu sieci i reguły preferencyjnego dołączania węzłów.
Niniejszy program pokazuje, ze rezygnacja z preferencyjnego dołączania węzłów przy zachowaniu rosnącego
charakteru sieci prowadzi do wykładniczego rozkładu stopni wierzchołków.
|
|
Model Straussa jako przykład
statystycznej zbiorowości grafów prostych
Program prezentuje zachowanie się modelu Straussa dla N=100 wezłów.
W modelu tym Hamiltonian grafu ma postać:
H(G)=t*m(G)-a*T(G),
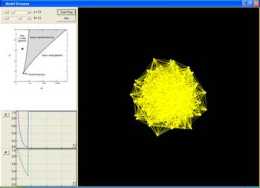 gdzie m(G) - liczba krawedzi, a T(G) - liczba trójkatów w grafie G.
W prawej czesci ekranu rysowany jest aktualny graf (rozmiar wezla odzwierciedla jego stopień).
W lewym dolnym rogu ekranu wykreślana jest aktualna unormowana liczba trójkatów
oraz unormowana liczba krawędzi. Diagram fazowy w lewej części ekranu ukazuje ciekawą
własność modelu: w zależności od wartości dwóch parametrów modelu, t oraz a,
siec moze przebywać w jednej z dwóch faz: pierwszej - o małej gęstości połączeń oraz
drugiej - o maksymalnej gęstosci (graf pelny). Aby zaobserwować pętle histerezy charakterystyczną
dla przejścia fazowego pierwszego rodzaju należy ustalić wartość parametru t, np. t=3,
i stopniowo zwiekszać wartość parametru a. Dla a bliskiego 100 następuje gwałtowny wzrost
liczby krawedzi (powstaje graf pelny). Zmniejszając następnie wartość parametru a uzyskujemy
gwałtowny spadek liczby krawędzi przy innej wartości a~7. Innymi słowy, w obszarze
7 < a < 100 stan układu zależy od jego historii, co jest cechą charakterystyczną dla przejścia fazowego tego typu. |
|
Model Isinga na strukturze dwóch sieci przypadkowych
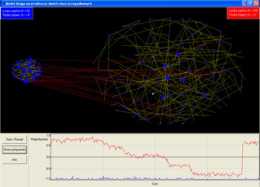 Model Isinga przeznaczony jest do opisywania własności materiałów magnetycznych.
Może on także slużyć jako prosty model formowania się opinii w społeczeństwie.
Spiny Isinga (s = +1 lub -1) mogą reprezentować opinie poszczególnych jednostek,
które tworząc pewną społeczną sieć oddziaływań, wpływają na opinie innych jednostek.
Niniejsza symulacja przedstawia formowanie sie opinii w dwóch sieciach o poczatkowo przeciwnych poglądach.
W miarę dodawania połączeń między węzłami jednej i drugiej sieci, każda z nich odczuwa coraz większy
wpływ opinii przeciwnej sieci. W pewnym momencie następuje gwałtowna zmiana uporządkowania
jednej z sieci (węzły tej sieci przyjmują opinię węzłów drugiej z sieci). Najciekawszą obserwacją
jest fakt, że pięciokrotnie mniej liczna sieć z lewej strony jest w stanie zmienić opinię
w znacznie większej sieci z prawej strony. Wynika to z faktu, że największy wplyw na stabilność
sieci ma jej spójność (liczba krawedzi), a nie rozmiar. Aby zaobserwować ten efekt, należy dodać
kilkanaście krawędzi obserwując jednocześnie magnetyzacje (czyli średnią opinię) na wykresie
w dolnej części ekranu. W pewnym momencie dodatnia magnetyzacja większej sieci zmienia znak na ujemny.
|
|
|
