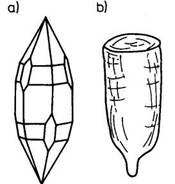
Rys. 4. Monokryształy szafiru: a) naturalny, b) otrzymany metodą Verneuila.
Kryształy
Pojęcie kryształu zawsze kojarzy się z mniej lub bardziej regularnym wielościanem,
jednakże definicja kryształu jest nieco inna. Kryształem nazywamy
ugrupowanie przestrzenne atomów, jonów, lub cząsteczke, wykazujące prawidłową
okresowość w różnych kierunkach otoczone płaskimi ścianami, tworzącymi wypukły
wielościan. Definicja ta zastała podana w 1945 roku przez A. F.
Wellsa. Na jej podstawie tej definicji można stwierdzić, że najistotniejszą
cechą kryształu jest prawidłowość jego budowy wewnętrznej. Należy jednak rozróżnić
ciała krystaliczne lub krystality,
które są ograniczone przypadkowymi powierzchniami krzywymi od kryształów ograniczonych
naturalnymi płaskimi ścianami. Ciała krystaliczne mają wiele interesujących
właściwości elektrycznych, magnetycznych, optycznych i mechanicznych, którymi
różnią się od innych ciał w stałym stanie skupienia, zwanych ciałami bezpostaciowymi.
Wszystkie właściwości ciał krystalicznych wynikają z ich specyficznej budowy
wewnętrznej, polegającej na trójwymiarowym, nieskończonym uporządkowaniu atomów
(jonów, cząsteczek). Pojedynczy, nie wykazujący zrostów, pęknięć i wyrostków
kryształ nazywamy monokryształem. Ciało
polikrystaliczne (polikryształ) składa się z licznych kryształów
lub krystalitów o mikroskopowych rozmiarach.
Naturalne kryształy np. szafiru (chemicznie szafir jest tlenkiem glinu, zawierającym
niewielką domieszkę tlenku tytanu i tlenku żelaza) otoczone są naturalnymi płaskimi
ścianami. Monokryształy rubinu czy szafiru otrzymywane metodą Verneuila mają
kształt „gruszki". Syntetycznie otrzymane „gruszki" są ciałami krystalicznymi
o takim samym składzie chemicznym, jak naturalny szafir.
 |
Rys. 4. Monokryształy szafiru: a) naturalny, b) otrzymany metodą Verneuila. |
Wspólną cechą, łączącą zewnętrznie różne — syntetyczną „gruszkę"
(krystalit) i naturalny kryształ szafiru, jest ich jednakowa budowa wewnętrzna.
Ze względu na sposób otrzymywania monokryształów, substancje je tworzące dzielimy
na rozpuszczalne i nierozpuszczalne. Rozpuszczalne to większość związków organicznych,
organicznych a także soli i kompleksów nieorganicznych, do drugiej grupy zalicza
się np. metale.
Monokryształy związków rozpuszczalnych hoduje się z roztworów. W tym celu przygotowuje
się roztwór badanej substancji zbliżony do nasyconego i wprowadza się zarodek
krystalizacji, a następnie roztwór doprowadza się do stanu lekkiego przesycenia
poprzez stopniowe obniżanie temperatury lub odparowanie rozpuszczalnika.
Forma zewnętrzna otrzymanego monokryształu zależy od badanego związku. Ogólny
kształt kryształu i jego wielkość zależą od warunków procesu krystalizacji,
jednakże w różnych kryształach tej samej substancji kąty pomiędzy ścianami pozostają
takie same. Istotna przy pomiarze jest wielkość monokryształu. Optymalna wielkość
zależy od szczegółów technicznych pomiaru, takich jak szerokość wiązki promieniowania
padającego i długość fali. Z jednej strony dąży się by kryształ był możliwie
duży, gdyż zazwyczaj skraca to czas pomiaru, z drugiej zaś im większy kryształ,
tym większa w nim absorpcja promieniowania rentgenowskiego. W praktyce wybiera
się monokryształy o wymiarach rzędu 0,2 – 0,6 mm.
 |
Fot. 1. Monokryształ kwarcu. |
 |
Fot. 2. Kryształ gipsu. |
 |
Rys. 3.Polkrystaliczny kwarc. |
 |
 |
Fot. 4. Monokryształy przed pomiarem rentgenowskim
przymocowane do szklanych kapilar. |
|
Źródła i charakterystyka promieniowania rentgenowskiego
Promieniowanie rentgenowskie powstaje w lampie rentgenowskiej podczas hamowania
szybkich elektronów padających na anodę. Tak powstałe promieniowanie tworzy
widmo ciągłe, któremu towarzyszy monochromatyczne spójne promieniowanie charakterystyczne
wykorzystywane w rentgenografii strukturalnej monokryształów. Widmo ciągłe powstaje
w wyniku emisji promieniowania hamowania, natomiast promieniowanie charakterystyczne
powstaje w wyniku wzbudzenia elektronów materiału anody powodujące emisję promieniowania
nieciągłego o określonej długości fali. Jeśli przejście (powrót) elektronu związane
z emisją następuje pomiędzy powłokami sąsiednimi, to oznacza się je symbolem
α. Z punktu widzenia analizy strukturalnej najistotniejsze są
przejścia elektronów z poziomów elektronowych L na K oznaczane
symbolem Kα. Przejścia z poziomów niesąsiednich na K
oznacza się . Inne serie widmowe ze względu na niewielkie natężenie promieniowania
ciągłego nie znajdują zastosowania w rentgenografii. Rozkład natężenia promieniowania
ciągłego i charakterystycznego Kα i Kβ pokazuje
rysunek.
 |
Rys. 5. Rozkład natężenia promieniowania ciągłego
(1a) i charakterystycznego (1b). |
Jak wiadomo długości większości wiązań w związkach organicznych wynoszą 1 –
2 Å. Długość fali promieniowania charakterystycznego zależy od liczby
atomowej metalu, z którego jest wykonana anoda lampy rentgenowskiej i zmniejsza
się odwrotnie proporcjonalnie do kwadratu liczby atomowej. Proporcjonalnie do
jej kwadratu rośnie natomiast twardość (przenikliwość) promieniowania. Znane
są lampy rentgenowskie z anodami wykonanymi z żelaza, chromu, miedzi, molibdenu,
srebra i inne.
 |
Rys. 6. Schemat budowy lampy rentgenowskiej. |
Oddziaływanie z materią
Podczas przechodzenia przez kryształ promieniowanie ulega m. in. absorpcji i
rozpraszaniu. Zjawisko rozpraszania polega na wywoływaniu
przez fale elektromagnetyczne drgań zewnętrznych elektronów atomów substancji
rozpraszającej. Drgające elektrony stają się źródłem wtórnych fal elektromagnetycznych,
o tej samej długości fali co fala padająca, rozchodzących się we wszystkich
kierunkach przestrzeni. Tego rodzaju rozpraszanie nazywa się spójnym lub koherentnym.
Promienie w ten sposób rozproszone przez elektrony atomów ciał krystalicznych
mogą ze sobą interferować. Interferencja promieni rozproszonych podlega prawidłowościom
związanym z wewnętrzną budową kryształów.
Przy pochłanianiu (absorpcji) cała
energia kwantu zostaje oddana elektronowi i w rezultacie kwant całkowicie zanika
— zostaje pochłonięty. Pochłonięciu kwantu towarzyszy wybicie — poza obręb atomu
— elektronu z jednej z powłok elektronowych atomu.
Jeżeli kwanty padających promieni rentgenowskich mają dostateczną energię, to
mogą one wybijać elektrony znajdujące się na powłokach wewnętrznych (K,
L,...). Wzbudzone w ten sposób atomy będą emitować wtórne promienie
rentgenowskie, rozchodzące się we wszystkich kierunkach. To wtórne promieniowanie
nazywa się rentgenowskim promieniowaniem fluorescencyjnym.
W doświadczalnych metodach krystalografii rentgenowskiej wzbudzenie w badanym
krysztale promieniowania fluorescencyjnego jest zjawiskiem niepożądanym, gdyż
powoduje dodatkowe (często bardzo silne) ogólne zaczernienie błony fotograficznej.
Kwanty promieniowania rentgenowskiego, wybijając elektrony z najbardziej zewnętrznych
powłok elektronowych atomu, powodują powstawanie fluorescencji w obszarach nadfioletowym,
widzialnym lub podczerwonym widma.
Osłabienie promieni rentgenowskich przy przechodzeniu przez materię określa
tzw. liniowy współczynnik osłabienia µ, będący
sumą współczynnika rozpraszania σ i współczynnika absorpcji właściwej
τ: µ = σ + τ. Dzieląc µ przez gęstość
D otrzymuje się tzw. masowy współczynnik osłabienia
µ/D = σ/D + τ/D charakterystyczny dla danej
substancji.
Współczynnik rozpraszania σ jest prawie
niezależny od długości fali i natężenia promieni pierwotnych oraz od rodzaju
naświetlanej substancji. Wartość jego jest niewielka i znacznie mniejsza od
współczynnika absorpcji. σ/D jest tzw. masowym współczynnikiem
rozpraszania. Współczynnik absorpcji właściwej
zależy od rodzaju naświetlanych atomów i od długości fali promieniowania λ.
τ/D jest tzw. masowym współczynnikem absorpcji.
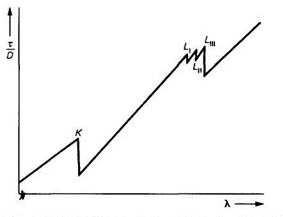 |
Rys. 7. Zależność masowego współczynnika absorbcji
τ/D od długości fali promieniwania rentgenowskiego; K,
LI, LII, LIII - progii absorbcji |
Krzywa zależności masowego współczynnika absorpcji dla danego rodzaju atomów
od długości fali promieni rentgenowskich ma charakterystyczny kształt. Jak widać
z rysunku, absorpcja maleje wraz ze zmniejszaniem się długości fali promieniowania.
Przy ściśle określonych długościach fal następują skokowe zmiany absorpcji,
w postaci tzw. progów (krawędzi) absorpcji K,L,..., związane
z granicznymi warunkami pochłaniania kwantów przez różne powłoki elektronowe
atomów. Występowanie trzech progów serii L(LI, LIII, LIII)
spowodowane jest niewielkimi różnicami energii trzech poziomów powłoki elektronowej
L atomu.
Ponieważ pochłanianie i rozpraszanie zachodzą w atomach, więc oczywiste jest,
że osłabienie natężenia promieni rentgenowskich przy przechodzeniu przez dowolną
substancję zależy od rodzaju i liczby atomów wchodzących w skład danego ciała
i prawie nie zależy od tego, czy dane atomy tworzą związek chemiczny czy też
mechaniczną mieszaninę.
Kierunek rozchodzenia się wiązki promieni rentgenowskich
ugiętych na sieci przestrzennej kryształu
Teoria Lauego
W teorii Lauego rozpatrywana jest dyfrakcja promieni rentgenowskich na sieci
przestrzennej kryształu, przy przyjęciu następujących założeń upraszczających:
Atomy w krysztale ułożone są według idealnego schematu sieci przestrzennej.
Atomy są nieruchome, tzn. nie wykonują drgań cieplnych. Promieniowanie rentgenowskie
padające na kryształ uginane jest przez każdy z atomów, a czynnikiem rozpraszającym
promienie rentgenowskie są elektrony. Wszystkie elektrony danego atomu w sieci
skupione są w jednym punkcie (w węźle sieci przestrzennej), tworząc jakby jedną
cząstkę o zdolności rozpraszania promieni rentgenowskich proporcjonalnej do
liczby skupionych elektronów. Promieniowanie rentgenowskie padając na sieć przestrzenną
powoduje, że elektrony wykonują drgania w takt drgań pola elektromagnetycznego
promieni. Dzięki tym drganiom elektrony stają się źródłem wtórnych fal o długości
takiej samej jak długość fali promieniowania padającego. Wtórne fale rozchodzą
się kuliście od poszczególnych węzłów sieci przestrzennej, przy czym w pewnych
ściśle określonych kierunkach kuliste fale wtórne w wyniku interferencji ulegają
wzmocnieniu, co doprowadza do powstawania tzw. wzmocnionych promieni interferencyjnych.
Promienie te w doświadczeniach obserwujemy jako promienie ugięte, tzn. odchylone
od kierunku wiązki promieni padających. Dyfrakcja polega więc na interferencyjnym
wzmacnianiu promieniowania rozproszonego.
Przyjmijmy, że wiązka równoległych promieni rentgenowskich pada na prostą sieciową,
w której punktowych węzłach znajdują się elektrony. Wszystkie fale rozproszone
na tych węzłach w pewnym określonym kierunku mają jednakowe amplitudy drgań
(jeśli każdy węzeł ma taką samą zdolność rozpraszania). Każda kolejna rozproszona
fala spóźnia się w fazie względem poprzedniej o stale taką samą wartość (mniejszą
od długości fali) i w rezultacie fale rozproszone są niezgodne w fazie. W przypadku
dostatecznie dużej liczby węzłów na prostej sieciowej prowadzi to do tego, że
w wyniku interferencji fal amplituda fali wypadkowej — poza jednym przypadkiem
— równa jest zero, czyli następuje całowity zanik pola elektromagnetycznego.
Rezultat interferencji fal jest różny od zera tylko wtedy, gdy różnica dróg
fal rozproszonych przez sąsiednie węzły stanowi całkowitą i taką samą liczbę
długości fali. Wówczas bowiem wszystkie fale rozproszone są zgodne w fazie i
amplituda wypadkowa jest równa arytmetycznej sumie wszystkich amplitud, czyli
fale rozproszone zostają wzmocnione. Tak więc w wyniku interferencji fal rozproszonych
na węzłach prostej sieciowej, promienie ugięte mogą rozchodzić się tylko w tych
kierunkach, w których różnica dróg fal rozproszonych przez dowolne dwa węzły
jest równa całkowitej liczbie długości fal.
Niech wiązka równoległych promieni rentgenowskich R pada pod kątem
α0 na prostą sieciową o periodzie identyczności a.
Wiązka ta zostaje ugięta (tzn. powstaje wzmocniony promień interferencyjny R')
pod kątem α w stosunku do prostej sieciowej (rys. 8). Jak wynika
z rysunku, zgodne w fazie promienie 2 i 3 dochodzą do węzła A prostej
sieciowej wspólnym czołem fali. Wzdłuż odcinków AC i DB promienie
te mają do przebycia niejednakowe drogi. Różnica odcinków AC i DB
stanowi różnicę dróg AS promieni 2 i 3: AS = AC —
DB.
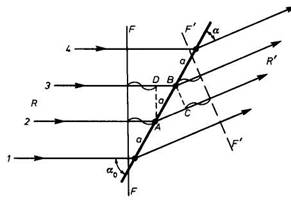 |
Rys. 8.Ugięcie promieni rentgenowskich na prostej
sieciowej; R — wiązka pierwotna promieni rentgenowskich, R'
— wiązka wtórna, AC—DB — różnica dróg, 1,2,... — promienie
rentgenowskie w wiązce, FF — czoło fali padającej, F'F'
— czoło fali ugiętej |
Z poprzednich rozważań wynika, że na to, aby nastąpiło interferencyjne wzmocnienie
promieni rozproszonych, różnica dróg między promieniami rozproszonymi na sąsiednich
węzłach prostej sieciowej musi być równa całkowitej wielokrotności długości
fali, czyli: AS = Hλ, gdzie H — liczba całkowita,
λ — długość fali. Ponieważ: AC = acosα,
DB = acosα0, więc AS = a(cosα
—cosα0).
a(cosα —cosα0) = Hλ
Równanie to jest tzw. równaniem Lauego, określającym kierunek rozchodzenia się wzmocnionego promienia interferencyjnego w przypadku ugięcia promieni rentgenowskich na prostej sieciowej. We wszystkich innych kierunkach, nie odpowiadających temu równaniu, przy dostatecznej liczbie węzłów na prostej sieciowej, promienie zostają wygaszone.
Interaktywna demonstracja Interferencji fal. |
W wyniku dyfrakcji powstaje tzw. obraz dyfrakcyjny
prostej sieciowej utworzony przez ugięte promienie rentgenowskie.
Teoria Braggów-Wulfa
Zjawisko ugięcia promieni rentgenowskich na sieci przestrzennej, w sposób znacznie
prostszy niż uczynił to M. v.Laue, zinterpretowali W. L. Bragg i W. H. Bragg
oraz G. W. Wulf. Według tej teorii płaszczyzna sieciowa jest więc traktowana
jako półprzezroczyste zwierciadło, od którego odbija się część promieni rentgenowskich.
Wobec tego, do interpretacji zjawiska ugięcia promieni rentgenowskich na sieci
przestrzennej dogodne może być przedstawienie jej jako zbioru wielu rodzin płaszczyzn
sieciowych o różnych wskaźnikach h, k, l i — co za
tym idzie o różnych odległościach międzypłaszczyznowych d(hkl).
Traktując sieć w taki właśnie sposób, Braggowie i Wulf stwierdzili, że zjawisko
powstawania wzmocnionego promienia interferencyjnego można przedstawić jako
odbicie wiązki promieni rentgenowskich od zespołu równoległych płaszczyzn sieciowych
(hkl). Odbicie to ma jednak szczególny charakter ze względu na to,
że w istocie jego przyczyną jest wtórne promieniowanie atomów, na które padają
promienie rentgenowskie; z tego też powodu nazwane zostało odbiciem interferencyjnym.
Rozważania tego rodzaju doprowadziły Braggów i Wulfa do określenia kierunku
rozchodzenia się wzmocnionego promienia interferencyjnego za pomocą jednego
równania.
Niech na rodzinę płaszczyzn sieciowych (hkl) o odległości międzypłaszczyznowej
d(hkl). pada wiązka promieni rentgenowskich R (rys.
9). Wiązka ta pada na płaszczyznę (hkl) pod kątem połysku θp.
Wiązka częściowo ulega interferencyjnemu odbiciu od płaszczyzny 1,
a częściowo wnika w głąb kryształu, ulegając interferencyjnemu odbiciu od głębiej
położonych płaszczyzn 2,3,4.
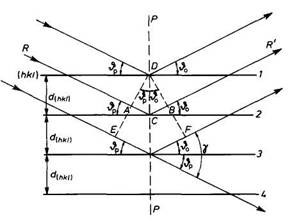 |
Rys. 9. Wyprowadzenie równania Bragga-Wulfa; θp
— kąt połysku, θ0 — kąt odbłysku, γ
— kąt ugięcia (γ = 2θ), PP — prostopadła
padania, R — wiązka padająca, R' — wiązka odbita, 1,2,3...
— kolejne płaszczyzny odbijające; DE, DF— czoło fali,
AC + CB — różnica dróg AS |
Interferencyjne odbicie następuje pod kątem odbłysku θ0, przy czym kąty połysku i odbłysku są sobie równe (θp = θ0), a promień padający R, promień odbity R' i prostopadła padania PP leżą w jednej płaszczyźnie prostopadłej do odbijających promienie płaszczyzn sieciowych. Promień padający R i promień odbity R' tworzą ze sobą kąt γ = 2θ (tzw. kąt ugięcia).
Odbite od kolejnych płaszczyzn sieciowych
promienie ulegają interferencyjnemu wzmocnieniu wtedy, gdy różnica dróg (AS)
promieni odbitych od dowolnych dwóch równoległych do siebie płaszczyzn sieciowych
jest równa całkowitej wielokrotności długości fali (nλ) promieni (warunek
Bragga-Wulfa).
Na rysunku 9, różnicy dróg promieni odbitych od płaszczyzn sieciowych 1 i 2 odpowiada suma odcinków AC i CB, czyli: AS = AC + CB. Z warunku Bragga-Wulfa wynika, że:
ΔS = nλ
gdzie n (= 1,2,3,...) jest rzędem odbicia. Ponieważ CD = d(hkl), wiec AC = CB = d(hkl)sinθ(hkl) i ostatecznie otrzymuje się:
nλ = 2d(hkl)sinθ(hkl)
Równanie to jednoznacznie określa kierunek rozchodzenia się wzmocnionego promienia
interferencyjnego, tj. promienia odbitego. Równanie to nazywa się równaniem
Bragga-Wulfa.
Interaktywna demonstracja teorii Braggów. |
Z równania Bragga-Wulfa wynika, że odbicie promieni rentgenowskich od płaszczyzn
sieciowych sieci przestrzennej ma charakter selektywny, tzn. występuje tylko
pod pewnymi kątami θ, ściśle określonymi dla płaszczyzn sieciowych
danej sieci przestrzennej i dla danej długości fali promieniowania λ.
Warto podkreślić, że w teorii Braggów-Wulfa kierunek rozchodzenia się wiązki
ugiętej określony jest za pomocą tylko jednego kąta, a nie trzech, jak to jest
w teorii Lauego.
W ujęciu teorii Braggów-Wulfa zaczernione plamki na rentgenogramach
(tzn. zarejestrowanych na błonach fotograficznych obrazach dyfrakcyjnych kryształów)
są śladami wiązek promieni rentgenowskich odbitych od płaszczyzn sieciowych
(hkl). Plamki te nazywa się refleksami.
W krystalografii rentgenowskiej refleksy charakteryzuje się za pomocą wskaźników
płaszczyzn sieciowych (hkl) odbijających promieniowanie, pomnożonych
przez rząd odbicia n. Otrzymane w ten sposób liczby nh, nk,
ni nazywają się wskaźnikami refleksów i nie muszą być względem siebie
liczbami pierwszymi.
Równania Lauego i Braggów Wulfa opisują fedno i to samo zjawisko interferencji
promieni rentgenowskich przez elektrony atomów tworzących sieć krystaliczną.
Natężenie promieniowania odbitego przez monokryształ zależy od następujących czynników: