Jeśli fala elektromagnetyczna jest w stanie pobudzić Twój telefon komórkowy do działania, to musi przenosić energię z jednego miejsca przestrzeni do drugiego. Wiemy już jak wiąże się gęstość energii pola elektrycznego z natężeniem tego pola, wzór (3.4.6) lub (3.4.6), oraz gęstość energii pola magnetycznego z wartością wektora indukcji, wzór (6.4.5).Gęstość energii, to energia przypadająca na jednostkę objętości. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego

(9.5.1)

gdzie E i B są wartościami natężenia pola elektrycznego i indukcji pola magnetycznego w danym punkcie przestrzeni w dowolnym momencie czasu. Pamiętając, że oraz, że możemy wzór (9.5.1) przepisać w postaci

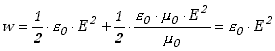(9.5.1a)

gdzie wyraziliśmy gęstość energii w funkcji natężenia pola elektrycznego. Jest to dokładnie dwukrotnie więcej niż wkład składowej pola elektrycznego, czyli oba pola mają jednakowy wkład do energii pola elektromagnetycznego. Możemy oczywiście wyrazić także gęstość energii w funkcji wartości wektora indukcji pola magnetycznego

.

(9.5.1b)

Podobnie możemy zapisać wyrażenie na gęstość energii w funkcji E i B 

.

(9.5.1c)

Określmy teraz energię transportowaną przez falę elektromagnetyczną w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów i . W czasie dt fala przesuwa się o odcinek . Przez powierzchnię S prostopadłą do kierunku rozchodzenia się fali przetransportowana jest energia zawarta w objętości . Energia ta wynosi . Energia przenoszona przez jednostkową powierzchnie w jednostce czasu wynosi więc

(9.5.2)

Wykorzystując znów związki: oraz możemy wzór (9.5.2) przepisać w postaci

(9.5.2a)

Energia ta przenoszona jest w kierunku prostopadłym do wektorów  i . Możemy więc zdefiniować wektor którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Pamiętając, że wektory i są do siebie prostopadłe zapisujemy wzór (9.5.2.a) w postaci wektorowej

(9.5.3)

 Określony wzorem (9.5.3) wektor nosi nazwę wektora Poyntinga.