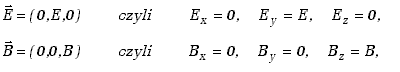
Zapiszmy równania Maxwella dla przypadku, kiedy w przestrzeni nie ma ładunków  ani ośrodków materialnych, tj. dla próżni. Przyjmijmy, że istniejące w przestrzeni pola: elektryczne i magnetyczne są do siebie prostopadłe. Niech kierunek pola elektrycznego pokrywa się z osią Y prostokątnego układu współrzędnych, a pola magnetycznego z osią Z. Zapiszemy to w postaci

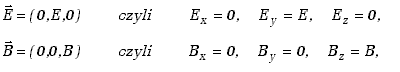(9.4.1)

Będziemy rozważali propagację zaburzeń pól w jednym kierunku, wzdłuż  osi X, z czego wynika, że pola te są jednorodne w kierunkach prostopadłych do kierunku propagacji. Oznacza to, że

(9.4.2)

czyli, że wartości E i B nie zależą od położenia punktu w kierunkach Y i Z, tzn. w każdym momencie mają te same wartości we wszystkich punktach leżących w płaszczyźnie YZ; zależą natomiast od X oraz t. Dla znalezienia związków pomiędzy zmianami pola w czasie i w kierunku X skorzystamy z równań Maxwella w postaci różniczkowej. 

Na podstawie pierwszego równania Maxwella, wzór (8.1.6)  możemy napisać 

(9.4.3)

gdzie wektor rotacji pola elektrycznego wyraziliśmy we współrzędnych prostokątnych , wzór (1.6.4) i skorzystaliśmy z warunków określonych wzorami  (9.4.1) i (9.4.2).  

Wykorzystując drugie równanie Maxwella zastosowane do naszych warunków otrzymujemy w podobny sposób

(9.4.4)

Zapiszmy pochodną cząstkową względem x dla obu stron równania (9.4.3)

(9.4.5)

Zapiszmy także pochodną cząstkową względem czasu dla równania (9.4.4)

(9.4.6)

Z równań (9.4.5) i (9.4.6) otrzymujemy związek

(9.4.7)

Związek ten będzie taki sam jak w znanym nam już równaniu falowym (9.2.6) jeżeli przyjmiemy, że

(9.4.8)

i podstawiając znane wartości oraz (patrz: INDEX, tablica stałych fizycznych) otrzymujemy

(9.4.8a)

Jest to prędkość rozchodzenia się fal elektromagnetycznych w próżni równa znanej nam prędkości światła (dokładna wartość podana jest w tablicy stałych fizycznych). Widzimy, że prędkość ta jest niezależna od częstości drgań czy długości fali. Jest to uniwersalna stała związana bezpośrednio z przenikalnością elektryczną i magnetyczną próżni -  podstawowymi charakterystykami pól: elektrycznego i magnetycznego. 

Wykonując różniczkowanie względem czasu dla równania (9.4.3) oraz względem x dla równania (9.4.4) otrzymujemy związek dla pola magnetycznego analogiczny do wzoru (9.4.7) dla pola elektrycznego

(9.4.9)

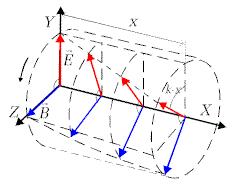
Stwierdziliśmy tu, że zmiany prostopadłych wzajemnie pól elektrycznego i magnetycznego mogą rozchodzić się w kierunku  prostopadłym do kierunku obu tych pól, i że zmiany te rozchodzą się z prędkością światła. Fale elektromagnetyczne są wiec falami poprzecznymi. Rozchodzenie się fali elektromagnetycznej ilustruje rysunek  9.4.1.

Równania (9.4.7)  i (9.4.9) są równaniami falowymi dla pola elektromagnetycznego. 

Równania te otrzymane są bezpośrednio z równań Maxwella. Podstawowe wnioski z nich wynikające sformułować można następująco.

2. Prędkość rozchodzenia się fal elektromagnetycznych w próżni jest uniwersalną stałą związaną z własnościami pól: elektrycznego i magnetycznego.

Propagacja pola elektrycznego i magnetycznego przebiega więc w ten sam sposób. Równania opisujące zmianę w przestrzeni (wzdłuż kierunku X) i w czasie obu pól i jednocześnie spełniające równania (9.4.7) oraz (9.4.9) można zapisać w ogólnej postaci

(9.4.10)

W przypadku fal sinusoidalnych, propagacja pól elektrycznego i magnetycznego opisana będzie równaniami

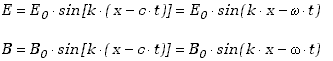(9.4.11)

gdzie . Amplitudy i nie są jednak niezależne, bowiem, relacja pomiędzy zmianami w przestrzeni i czasie obu pól dana jest wzorami (9.4.3) i (9.4.4). Obliczając pochodne 

(9.4.12)

i wstawiając otrzymane wyrażenia do wzoru (9.4.3) otrzymujemy związek pomiędzy amplitudami

(9.4.13)

(Ten sam związek uzyskuje się obliczając odpowiednie pochodne i wykorzystując związek (9.4.4).)

Mając na uwadze, że zmiany obu pól przebiegają w ten sam sposób dany równaniami (9.4.11) możemy związek pomiędzy amplitudami przenieść na relacje pomiędzy wartościami pól

(9.4.14)

Kiedy fala rozchodzi się w ośrodku materialnym, jej prędkość jest mniejsza i wiąże się z wartością prędkości światła w próżni i wartościami względnych przenikalności: elektrycznej i magnetycznej w ośrodku zależnością.

(9.4.15)

co jest bezpośrednią konsekwencją zamiany w tym przypadku przenikalności elektrycznej i magnetycznej.

Rozwiązanie równania falowego może być również  zapisane z użyciem funkcji cosinus, może być też uwzględniona dowolna wartość przesunięcia fazowego itd. Kierunki wektorów i mogą być też inne niż przyjęliśmy to w równaniach (9.4.1) jeśli tylko zachowane będą relacje pomiędzy nimi. Na przykład, jeśli pole elektryczne  skierowane jest wzdłuż osi Z, to pole magnetyczne skierowane będzie w kierunku -Y.  Rozwiązanie równania falowego ma w takim przypadku postać. 

(9.4.16)

 Kiedy drgania wektora zachodzą tylko w jednej płaszczyźnie (i to samo dotyczy wektora ) to mówimy, że fala taka jest falą płaską. 

Kiedy z zachowaniem wzajemnych relacji kierunkowych, układ wektorów i wykonuje obrót wokół kierunku propagacji, to mówimy, że fala jest spolaryzowana kołowo. W zależności od kierunku tego obrotu fala może być spolaryzowana prawo-  lub lewoskrętne . W przypadku fali spolaryzowanej kołowo składowe Y i Z wektorów i będą różne w różnych punktach na osi X, przy zachowaniu bezwzględnych ich wartości. Ilustruje to Rys.9.4.2. Kiedy  bezwzględne wartości zmieniają się, mówimy o polaryzacji eliptycznej.

Rys.9.4.2. Fala elektromagnetyczna spolaryzowana kołowo

 Składowe Y i Z dla fali spolaryzowanej kołowo  mogą być zapisane w postaci 

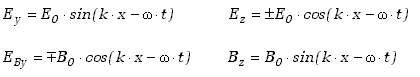(9.4.17)

Dwie różne kombinacje znaków odpowiadają dwóm kierunkom polaryzacji kołowej.