Omawiając zjawisko indukcji elektromagnetycznej w lekcji szóstej pokazaliśmy, że w przewodniku, który poruszając się przecina linie indukcji pola magnetycznego pojawia się siła elektromotoryczna. Wartość indukowanej SEM jest proporcjonalna do szybkości przecinania przez przewodnik linii indukcji pola magnetycznego, a kierunek zgody z regułą Lenza. Efekt ten objaśniliśmy działaniem na ładunki siły Lorentza pod wpływem której następuje ich przemieszczenie się, co powoduje w konsekwencji pojawienie się różnicy potencjałów.

Czy jednak właśnie taki jest mechanizm powstawania siły elektromotorycznej? Może nasze objaśnienie jest konsekwencją innego, bardziej ogólnego prawa? Przypuszczenie to wydaje się uzasadnione, jeśli weźmiemy pod uwagę fakt doświadczalny, że siła elektromotoryczna indukcji pojawia się także w nieruchomych obwodach zamkniętych znajdujących się w zmiennym polu magnetycznym (trzeci przykład we wstępie do lekcji szóstej). Przecież pole magnetyczne na nieruchome ładunki nie działa i w ruch wprawić ich nie może (?!) Co wiec wywołuje wtedy ruch ładunków?

Siła Lorentza napisana dla pól elektrycznego i magnetycznego, wzór (5.2.2) zawiera też człon związany z polem elektrycznym, które działa na ładunki tak w ruchu, jak i w spoczynku. W rozważanym przypadku pole elektryczne jednak nie występuje. Otóż Maxwell założył, że ... występuje, a mówiąc ściślej, że zmienne pole magnetyczne wywołuje powstawanie w przestrzeni pola elektrycznego. Przy takim podejściu powstająca siła elektromotoryczna i prąd płynący w zamkniętym obwodzie są jedynie wskaźnikami tego, że w przestrzeni istnieje pole elektryczne. 

Jaki jest związek pomiędzy zmianami pola magnetycznego a pojawiającym się wskutek tego polem elektrycznym?

Związek pomiędzy siłą elektromotoryczną w obwodzie zamkniętym a natężeniem pola sił zewnętrznych dany jest wzorem (4.4.5).  Sumaryczne pole w przewodniku posiada też składową sił elektrostatycznych, wzór (4.4.2), z czego wynika, że

Siła elektromotoryczna może wiec być zapisana jako różnica

Pamiętamy jednak, że pole sił elektrostatycznych jest polem potencjalnym, co oznacza, że  (patrz wzór (2.3.24))

Wynika z tego, że siła elektromotoryczna indukowana w obwodzie zamkniętym równa jest cyrkulacji wektora natężenia pola po tym obwodzie.

Zmiana w czasie strumienia indukcji pola magnetycznego przechodzącego przez zamknięty kontur może następować z różnych powodów. Może to być zmiana położenia konturu lub jego kształtu, może być to również zmiana samego pola w czasie. To, że chodzi o zależność od czasu, zapisujemy w postaci pochodnej cząstkowej. Wzór (6.1.7) dla zamkniętego konturu zapiszemy wiec w postaci.

 Wzór ten wyraża związek pomiędzy zmianami strumienia indukcji pola magnetycznego a powstającym wskutek tego polem elektrycznym. Związek ten można również wyrazić w postaci różniczkowej wykorzystując twierdzenie Stokesa, wzór (1.7.2) i zamieniając całkowanie po konturze na całkowanie po powierzchni przez ten kontur obejmowanej oraz  korzystając z faktu, że pole powierzchni konturu może być dowolne. Otrzymujemy wówczas związek

Nie znikanie rotacji natężenia pola elektrycznego oznacza, że pole to jest polem wirowym (patrz segment 6 w lekcji 1). Z drugiej strony pamiętamy, patrz wzór (2.3.26), że pole elektrostatyczne jest polem potencjalnym, a więc bezwirowym. Oba pola różnią się więc od siebie zasadniczo. 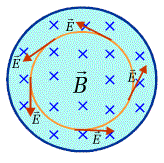Linie sił pola elektrostatycznego zaczynają się i kończą na ładunkach elektrycznych, natomiast  linie sił indukowanego pola elektrycznego, podobnie jak linie indukcji pola magnetycznego, nie mają początku ani końca; są liniami zamkniętymi, patrz Rys. 8.3.1., który pokazuje wektory natężenia pola elektrycznego w kilku  punktach  pola magnetycznego rosnącego w czasie . Spoglądając na rysunek pamiętajmy właśnie o tym. Strumień pola magnetycznego nie może być stały; musi zmieniać się w czasie, czego nie można pokazać na statycznym rysunku.

Rys.8.3.1. Wirowe pole elektryczne

Rozważania nasze prowadzą do wniosku, że efektem pierwotnym zmian pola magnetycznego jest powstawanie wirowego pola elektrycznego, zaś siła elektromotoryczna indukcji i przepływający wskutek jej istnienia prąd są efektami wtórnymi. Inaczej mówiąc, związek pomiędzy zmianą w czasie pola magnetycznego i cyrkulacją pola elektrycznego po zadanym konturze wcale nie implikuje wymagania, że ma to być kontur przewodzący prąd. Wzory (8.3.5) oraz (8.3.6) stanowią całkową i różniczkowa postać kolejnego równania Maxwella, które słowami można wyrazić następująco

Zmienne pole magnetyczne wywołuje w każdym punkcie pola powstawanie wirowego pola elektrycznego