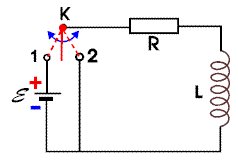
Obwód składa się ze źródła siły elektromotorycznej o zaniedbywanym oporze wewnętrznym, oporności R oraz indukcyjności L. Czerwonym kolorem pokazany jest przełącznik K, który może zajmować dwa położenia oznaczone cyframi 1 i 2. Kiedy przełącznik jest w  położeniu 1, zamknięty jest obwód zawierający źródło SEM. W obwodzie płynie prąd o natężeniu
		(6.3.1)
Rys. 6.3.1. Schemat obwodu RL

Zakładamy, że oporność (omowa) indukcyjności jest zaniedbywanie mała. W momencie czasu (t=0) zmieniamy położenie przełącznika do pozycji 2. Odłączenie SEM spowoduje zmianę strumienia indukcji i w konsekwencji pojawienia się siły elektromotorycznej samoindukcji, która zgodnie z regułą Lenza będzie przeciwstawiać się zanikowi prądu w obwodzie. Przez oporność R popłynie prąd I spełniający równanie, które możemy zapisać w postaci

lub w postaci równania różniczkowego o rozdzielonych zmiennych

Całkując obie strony tego równania otrzymujemy

gdzie jest stałą całkowania. Z równości (6.3.4) i własności logarytmów naturalnych wynika, że

Jak zwykle, do wyznaczenia stałej całkowania wykorzystujemy warunki początkowe pamiętając, że dla t=0 wartość prądu dana była wzorem (6.3.1). Podstawiając te wartości do wzoru ( 6.3.5) otrzymujemy rozwiązanie równania (6.3.3.) w postaci

Uzyskany rezultat pokazuje, że prąd w obwodzie będzie zanikał zgodnie z zależnością wykładniczą, zaś szybkość zanikania określona jest przez stosunek oporności do indukcyjności obwodu. Odwrotność tego stosunku, to stała czasowa obwodu RL, którą oznaczyliśmy symbolem ,

Im większa stała czasowa, tym wolniej zanika prąd w obwodzie. Kiedy jednak po rozwarciu obwodu pozostawiamy go otwartym, a indukcyjność jest duża, to wysokie indukowane napięcie powoduje powstawanie iskry lub łuku elektrycznego. 

Kiedy z kolei przełącznik przestawiamy z pozycji 2 do pozycji 1 mamy sytuację odwrotną. Zgodnie z reguła Lenza efekt pojawienia się SEM samoindukcji sprawi, że prąd będzie narastał powoli, a czas narastania określony będzie znów przez stałą czasową obwodu. Drugie prawo Kirchhoffa dla takiego obwodu zapiszemy w postaci

Rozwiązanie tego równania niejednorodnego (podane tu bez szczegółów rozwiązywania) ma postać

Równanie to określa szybkość narastania prądu w obwodzie z indukcyjnością L.

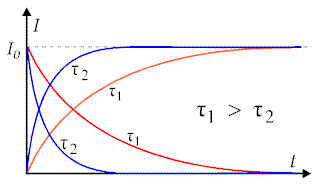Zależność zanikania i narastania prądu w obwodzie z indukcyjnością przedstawia Rys.6.3.2. dla dwóch różnych stałych czasowych. Rys.6.3.2. Zależności czasowe dla obwodu RL.