Wszystkie przypadki rozważane we wstępie do tej lekcji łączy jedna wspólna cecha. Prąd w zwoju przewodnika połączonego z galwanometrem pojawia się wówczas, gdy zmienia się strumień   wektora indukcji magnetycznej , przechodzący przez ten zwój. Fakt, że prąd nie płynął, kiedy magnes wsunięty był do środka zwoju oraz kiedy drugi zwój z prądem był w pobliżu świadczy o tym, że nie chodzi tu o samą obecność pola magnetycznego, ale o zmianę tego pola, która powoduje zmianę strumienia wektora indukcji. Fakt, że prąd pojawiał się także, kiedy zwoje pozostawały względem siebie nieruchome, a tylko włączany i wyłączany był prąd w zwoju obok, świadczy o tym, że chodzi tu o zmianę strumienia w czasie, a nie w przestrzeni,  Z kolei, aby galwanometr mógł wykazać przepływ prądu, musiała być wytworzona różnica potencjałów, czyli musiała pojawić się siła elektromotoryczna  na końcach przewodnika połączonego z galwanometrem. Związek pomiędzy zmianą w czasie strumienia  i wytworzoną siłą elektromotoryczną  zapisujemy w postaci równania

 Znak minus skomentujemy nieco później. Wzór (6.1.1) wyraża prawo indukcji Faradaya - fundament wiedzy o elektryczności oraz elektroenergetyki. Bez świadomości istnienia tego prawa żylibyśmy wciąż w epoce świecy i lampy naftowej...

Oczywiście, chcielibyśmy, by było jak największe. Możemy to osiągnąć stosunkowo łatwo powiększając liczbę zwojów przewodnika uzyskując wartość siły elektromotorycznej proporcjonalnej do liczby zwojów N,

 Pamiętać należy jednak, że w ten sposób powiększamy też opór obwodu i należy znaleźć optimum pomiędzy liczbą zwojów, a opornością całkowita obwodu. Innym sposobem powiększenia siły elektromotorycznej jest zwiększenie szybkości zmiany strumienia indukcji. Efekt taki osiągnąć można poprzez zwiększenie zmiany strumienia w przedziale czasu w którym ta zmiana zachodzi. Wynika to bezpośrednio z wzoru (6.1.1), który mówi, że wartość siły elektromotorycznej indukcji elektromagnetycznej jest określona przez szybkość zmian strumienia indukcji magnetycznej (pochodną   względem czasu).

Nadszedł czas na skomentowanie znaku minus w podanych wyżej wzorach. Przepływ prądu w obwodzie z galwanometrem spowoduje powstanie pola magnetycznego wokół tego obwodu. Pole to będzie z kolei powodować powstawanie siły elektromotorycznej w obwodzie pierwotnym. Powstanie rodzaj wielokrotnego sprzężenia zwrotnego, bowiem rozpatrywanie wzajemnego oddziaływania można kontynuować dalej. Są dwie możliwości: 1) wytworzone w obwodzie wtórnym pole magnetyczne będzie zwiększać zmianę strumienia pola magnetycznego, 2)  będzie ją zmniejszać. Który z tych wariantów realizuje  się w rzeczywistości?

Wniosek nasuwa się sam. W pierwszym przypadku otrzymalibyśmy zwiększanie zmian strumienia , a w konsekwencji, wzrost prądu płynącego przez galwanometr, bez wkładania w proces ten dodatkowej pracy. Przeczy to zasadzie zachowania energii i przypomina znane z termodynamiki "Perpetuum mobile". Zachowanie się obwodu w drugim przypadku przypomina zaś trzecią zasadę dynamiki Newtona i ten właśnie przypadek realizuje się w rzeczywistości..

Znak minus reprezentuje właśnie ten drugi przypadek. Powiążemy go nieco później z zasadą zachowania energii, ale już teraz sformułujemy regułę, która znak ten wyraża. Reguła ta została podana przez H. F. Lenza w 1834 roku i nosi nazwę reguły Lenza.

Indukowany prąd elektryczny ma taki kierunek, że przeciwstawia się zmianie strumienia pola magnetycznego, która go wywołuje.

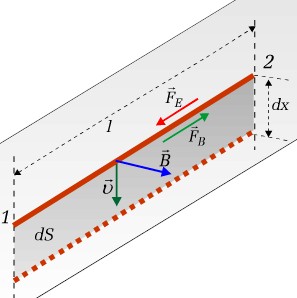Dla ilościowego wykazania prawa indukcji elektromagnetycznej rozważmy ruch z prędkością prostoliniowego odcinka przewodnika o długości w polu magnetycznym o indukcji , Rys.6.1.1.Przewodnik przesuwamy z góry w dół, a kierunek pola magnetycznego jest poziomy. Wektory i są więc wzajemnie prostopadłe.  Na rysunku zilustrowane jest przesunięcie o odcinek dx. Na swobodne elektrony w przewodniku działa siła Lorentza wynikająca z ich ruchu wraz z całym przewodnikiem . Elektrony będą przemieszczać się w kierunku od punktu 1 do punktu 2 (pamiętamy, że ładunek elektronów jest ujemny) . Wskutek ich przemieszczania zostaje naruszona równowaga ładunków w przewodniku i powstaje pomiędzy tymi punktami różnica potencjałów, .

Rys. 6.1.1. Mechanizm powstawania siły elektromotorycznej indukcji

Oznacza to, że w przewodniku pojawia się pole elektryczne, którego wartość liczbowa równa jest stosunkowi różnicy potencjałów do odległości pomiędzy punktami. 

a na elektrony działa siła elektrostatyczna przeciwdziałająca ich dalszemu przemieszczaniu się. Siła  ta ma kierunek przeciwny do siły  pochodzącej od ruchu przewodnika w polu magnetycznym. Sytuacja jest podobna do rozpatrywanego przez nas zjawiska Halla, z tą różnicą, że tam ruch elektronów wywołany był przyłożoną zewnętrzną różnicą potencjałów, a tu ich ruch w kierunku pionowym wywołany jest przyłożeniem do przewodnika zewnętrznej siły. W rezultacie osiągnięty zostanie stan,  w którym obie te siły będą się równoważyć elektrony przestaną się przemieszczać.  W stanie równowagi sumaryczna siła będzie więc równa zeru. Pamiętamy, że siła Lorentza dla przypadku działania na ładunki pola elektrycznego i magnetycznego ma postać podaną wzorem (5.2.2). (Obie siły działają wzdłuż jednej prostej wiec możemy stosować zapis skalarny.)

 Występująca tu różnica potencjałów, która spowodowana jest siłami zewnętrznymi (przemieszczaniem przewodnika w polu magnetycznym) odpowiada istnieniu w obwodzie siły elektromotorycznej . Zgodnie z prawem Ohma, wzór (4.4.5), zastosowanym tu do obwodu otwartego ( w którym I=0) mamy relację

Stąd na podstawie związków (6.1.3) i (6.1.4) otrzymujemy

Prędkość przemieszczania przewodnika można wyrazić w postaci otrzymując

Iloczyn jest polem powierzchni zakreślonej przez przewodnik w czasie , zaś iloczyn jest strumieniem indukcji przez powierzchnię . Uwzględniając te związki otrzymujemy 

Otrzymany rezultat jest właśnie prawem indukcji elektromagnetycznej sformułowanym przez Faradaya. W rozpatrywanym przez nas przypadku  siła elektromotoryczna indukcji jest równa zmianie strumienia indukcji magnetycznej przez powierzchnię zakreślaną przez przewodnik w jednostce czasu.