Zadanie 5.3 ruch ładunku w polu elektrycznym
wahadło matematyczne
Przypomnijmy sobie
wiadomości o ruchu wahadła z kursu Fizyki 1.
Wahadłem matematycznym nazywamy punkt materialny zawieszony
na nieważkiej i nierozciągliwej nici w polu grawitacyjnym. Jeśli wahadło
takie wychylimy z położenia równowagi, tak aby nić tworzyła z
kierunkiem pionowym (jest to kierunek działania siły grawitacji) kąt a,
to zacznie się ono wahać w płaszczyźnie pionowej.
Dla małych kątów a będzie to ruch
harmoniczny. Równanie charakteryzujące ten ruch ma postać:
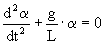 , ,
gdzie: g to przyśpieszenie grawitacyjne, L to długość nitki wahadła,
a to kąt wychylenia od położenia równowagi.
Okres wahań T0 dla takiego wahadła jest :
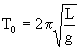 . . |
|
|
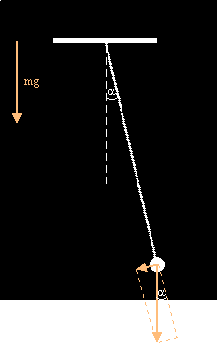
Rys.5.3.2. Wahadło matematyczne.
|
W naszym zadaniu, gdy nie ma oddziaływania elektrycznego tj.
- przy braku napięcia na kondensatorze U0 = 0 (wtedy też
natężenie pola elektrycznego E = 0 ponieważ
 ),
niezależnie od ładunku kulki,
),
niezależnie od ładunku kulki,
- gdy kulka nie jest naładowana, a przyłożone jest napięcie do okładek
kondensatora
to okres
wahań kulki równy jest T0
(to okres wahań wahadła matematycznego o długości L).
wahadło matematyczne w kondensatorze
Naładowana
kulka znajduje się w polu grawitacyjnym i w polu elektrycznym
wytworzonym w kondensatorze. Na kulkę oddziałuje Ziemia siłą grawitacji oraz
siła oddziaływania elektrostatycznego. Okres wahań kulki zależy od
wypadkowej Fw tych siły:
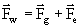 ,
,
gdzie 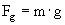 ,
,
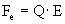 .
.
| Gdy
zwrot wektora E zgodny ze zwrotem wektora g to: |
Gdy
zwrot wektora E przeciwny do zwrotu wektora g to: |
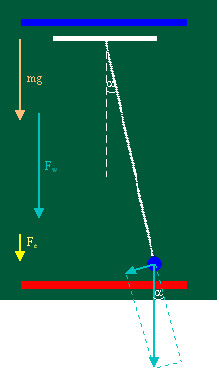 |
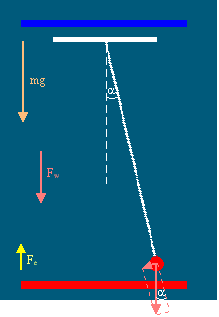
|
|
Wypadkowa siła Fw będzie miała wielkość
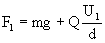 , ,
a przyspieszenie masy kulki odpowiednio
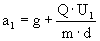 . .
Dlatego okres wahań 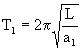 . . |
Wypadkowa siła Fw będzie
miała wielkość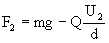 , ,
a przyspieszenie masy kulki odpowiednio
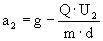 . .
Dlatego okres wahań 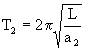 .
. |
|
Jeśli uwzględnimy, że dla wahadła matematycznego 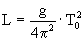 , ,
to: |
 . . |
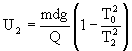 . . |
Poprzez zmianę polaryzacji okładek kondensatora uzyskujemy zmianę
zwrotu wektora natężenia pola elektrostatycznego. Okres wahań
kulki zależy od wypadkowej siły oddziaływania: siły grawitacji i siły
elektrostatycznej.
![]() ,
,![]() .
.


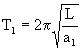 .
.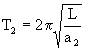 .
. .
.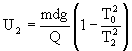 .
.