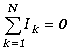
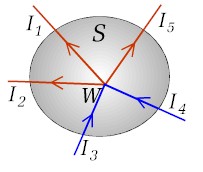
Na rysunku 4.5.1 pokazany jest przykładowy węzeł W gdzie zbiega się pięć przewodników. W dwóch z nich (zaznaczonych kolorem niebieskim) prądy płyną w kierunku do węzła, w trzech pozostałych kierunek prądu jest przeciwny. W węźle nie ma żadnego źródła więc z równania ciągłości wynika, że strumień gęstości prądu przez dowolną powierzchnię S zawierającą węzeł musi być równy zeru. Ten sam wniosek wynika z zasady zachowania ładunku. Będzie tak wtedy, kiedy suma prądów wpływających do węzła równa będzie sumie prądów wypływających. Jest to właśnie treść pierwszego prawa Kirchhoffa, które zapisujemy i wyrażamy w postaci
Rys. 4.5.1. Ilustracja pierwszego prawa Kirchhoffa		(4.5.1)

Algebraiczna suma prądów w węźle sieci równa jest zeru.

Przy sumowaniu, wartości prądów wpływających do węzła oznaczamy dodatnio, zaś wypływających ujemnie.

Drugie prawo dotyczy oczka sieci. Przykładowe oczko pokazuje rysunek 4.5.2. 

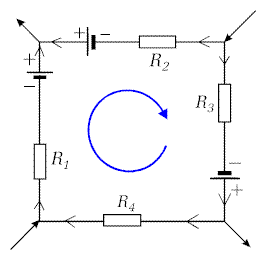	Elementami oczka są zarówno źródła siły elektromotorycznej jak i oporności. Ich liczba i układ może być całkowicie dowolny. Jeśli wybierzemy jakiś kierunek obiegu wokół konturu oczka, a następnie przypiszemy wszystkim prądom, których kierunek jest zgodny z obranym kierunkiem znak plus i odpowiednio prądom w kierunku przeciwnym - znak minus oraz wszystkim siłom elektromotorycznym występującym w oczku przypiszemy znak plus jeśli powodują one przepływ prądu wzdłuż obranego kierunku i znak minus - jeśli w kierunku przeciwnym, to związek pomiędzy sumą algebraiczną sił elektromotorycznych w oczku oraz sumą spadków napięć na występujących w oczku opornościach wyraża wzór stanowiący treść drugiego prawa Kirchhoffa
Rys. 4.5.2. Ilustracja drugiego prawa Kirchhoffa		(4.5.2)

 gdzie N jest liczbą odcinków na które kontur podzielony jest węzłami.

Prawo to sformułować można następująco.

Suma algebraiczna wszystkich sił elektromotorycznych w oczku sieci równa jest sumie występujących w tym oczku spadków napięć.