Rys. 3.4.3. Kondensator  z dielektrykiem

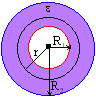
Jaka będzie pojemność kondensatora cylindrycznego o długości L, którego wewnętrzna okładka jest walcem o promieniu R₁, a zewnętrzna  - walcem o promieniu R₂, współosiowym z okładką wewnętrzną, wypełnionego dielektrykiem o  przenikalności e ? (Rys. 3.4.3.).

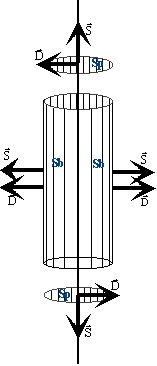
Pole elektryczne w takim kondensatorze będzie miało symetrię cylindryczną, a wektor D  kierunek radialny oraz stałą wielkość na powierzchni walca o dowolnym promieniu r.

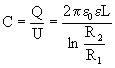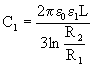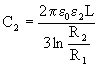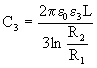Rys. 2.4.3. Strumień indukcji pola przez powierzchnię walca.

Do obliczenia  natężenia pola elektrycznego w takim kondensatorze zastosujemy prawo Gaussa. Niech zamknięta powierzchnia Gaussa będzie powierzchnią walca, współosiowego z kondensatorem, o długości L i promieniu r takim, że R₁ < r < R₂.
Strumień indukcji pola elektrycznego przez zamkniętą powierzchnię Gaussa jest sumą strumieni przechodzących przez powierzchnie jego podstaw Sp (górną i dolną) i powierzchnię boczną Sb :

,

gdzie dla wektorów prostopadłych iloczyny skalarne , a dla wektorów równoległych .

Dlatego też :

,

a z prawa Gaussa

,

gdzie Q jest ładunkiem, który otacza powierzchnia walca.

 wskazówka

rozwiązanie

 odpowiedź