![]() .
.
 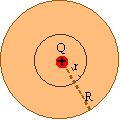
Rys. 3.2.3.Promień powłoki r mniejszy od promienia kuli R. |
Dla odległości r mniejszych od promienia R kuli wykonanej
z dielektryka, z prawa Gaussa
|
 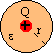
Rys. 3.2.4.Ładunek Q wewnątrz powłoki o promieniu r. |
Ładunek Q wewnątrz powłoki o promieniu r. |
Stąd indukcja pola elektrycznego maleje z odległością od środka kuli zgodnie z zależnością:
![]() ,
,
a natężenie pola wg wzoru
![]() .
.
 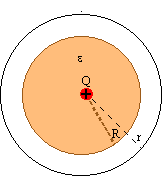
Rys. 3.2.5. Promień powłoki r większy od promienia kuli R. |
Dla odległości r większych od promienia R kuli wykonanej
z dielektryka, z prawa Gaussa
|
Stąd indukcja pola elektrycznego maleje z odległością od środka kuli zgodnie z zależnością:
![]() ,
,
Do obliczenia potencjału pola elektrostatycznego wykorzystamy zależność wiążącą potencjał i natężenie pola zachowawczego. Przyjmujemy, że potencjał pola w nieskończonej odległości od kuli jest równy zeru.
Ponieważ w tym obszarze ![]() to
to
![]() .
.
Ponieważ w tym obszarze ![]() to
to
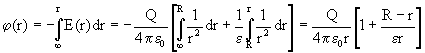 .
.
|
rozwiązanie |