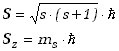Mówiliśmy już, że badania widm atomowych dostarczyły cennych informacji
o strukturze atomu i w historii rozwoju fizyki atomowej odegrały niezwykle ważną
rolę. Stanowiły najpierw eksperymentalne potwierdzenie słuszności modelu
Bohra w odniesieniu do wodoru a potem pokazały niedostatki tego
klasyczno-kwantowago opisu na przykładzie widma promieniowania helu. Na tym
jednak nie zakończyła się rola analizy struktury widm optycznych. Bardziej
precyzyjne obserwacje pokazały, ze linie początkowo uważane za pojedyncze składają
się w rzeczywistości z kilku linii. Nazwano to strukturą
subtelną widm. Początkowo przypuszczano, że jest to rezultat efektów
relatywistycznych, które nie są brane pod uwagę w równaniu Schrödingera.
Wkrótce jednak okazało się, że struktura subtelna pojawia się w takich
przypadkach, gdzie prędkości elektronów dalekie są od prędkości światła.
Równie zagadkowe okazały się wyniki doświadczenia Sterna i Gerlacha.
W 1922 roku Stern i Gerlach wykonywali pomiary, których zamiarem był
pomiar magnetycznego momentu dipolowego atomów srebra.
Jeżeli założy się, że moment magnetyczny istnieje, ale nie jest
skwantowany powinno otrzymać się rozciągnięcie poprzeczne wiązki po włączeniu
pola, jeśli jest skwantowany powinno się obserwować na ekranie szereg prążków.
Stern i Gerlach zaobserwowali rozszczepienie wiązki na dwa prążki,
jeden odchylony w gorę, drugi w dół. Środek odpowiadający brakowi
odchylenia pozostawał pusty. Z ich oszacowań wynikało, że odchylenie powinno
być proporcjonalne do składowej 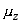 momentu magnetycznego, która z kolei proporcjonalna jest do składowej Lz
orbitalnego momentu pędu. Liczba prążków powinna odpowiadać liczbie
ustawień względem osi Z wektora momentu orbitalnego. Zawsze jednak
powinien byś prążek wiązki nieodchylonej, odpowiadający wartości ml
równej zeru. Tymczasem takiego prążka nie było. Wykonano wiele
wariantów doświadczenia, ale jego wynik pozostawał zawsze niezrozumiały przy
próbie interpretacji za pomocą tylko orbitalnego momentu magnetycznego.
momentu magnetycznego, która z kolei proporcjonalna jest do składowej Lz
orbitalnego momentu pędu. Liczba prążków powinna odpowiadać liczbie
ustawień względem osi Z wektora momentu orbitalnego. Zawsze jednak
powinien byś prążek wiązki nieodchylonej, odpowiadający wartości ml
równej zeru. Tymczasem takiego prążka nie było. Wykonano wiele
wariantów doświadczenia, ale jego wynik pozostawał zawsze niezrozumiały przy
próbie interpretacji za pomocą tylko orbitalnego momentu magnetycznego.
W 1925 roku Goudsmit i Uhlenbeck wystąpili z sugestia istnienia jeszcze
jednej liczby kwantowej przypisanej elektronowi. Liczba ta wiązałaby się z
momentem pędu elektronu wynikającym z jego obrotu wokół własnej osi. Taki własny
moment pędu nazwano spinem. Później okazało się,
że dosłowne traktowanie spinu jako momentu obrotowego jest nieuzasadnione.
Spin jest po prostu jedną z własności cząstki, podobnie jak masa, czy ładunek
elektryczny. Faktem jest jednak, że jego własności są bardzo podobne do własności
orbitalnego momentu pędu.
Wymieńmy więc podstawowe własności spinu. Jego wartość i rzut na wyróżnioną
(np. przez kierunek pola magnetycznego) oś są określone przez wyrażenia takie same jak wektora
orbitalnego momentu pędu, tylko z innymi liczbami kwantowymi.
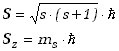 |
(13.5.1) |
gdzie czwarta liczba kwantowa 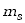 ,
zwana magnetyczną liczbą spinową, może przyjmować wartości od -s do +s czyli razem (2s+1)
wartości . Spinowy moment pędu dodaje się do orbitalnego momentu pędu. Całkowity
moment pędu
,
zwana magnetyczną liczbą spinową, może przyjmować wartości od -s do +s czyli razem (2s+1)
wartości . Spinowy moment pędu dodaje się do orbitalnego momentu pędu. Całkowity
moment pędu 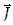 określony
jest więc przez momenty pędu: orbitalny i spinowy w następujący sposób:
określony
jest więc przez momenty pędu: orbitalny i spinowy w następujący sposób:
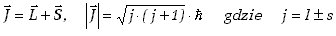 . . |
(13.5.2) |
Przypisując wynik doświadczenia Sterna-Gerlacha własnościom spinu
wyciągamy natychmiastowy wniosek, że skoro liczba linii na które rozszczepiła
się wiązka w doświadczeniu wyniosła dwa, to 2=2s+1 czyli
s=1/2. Liczba kwantowa 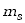 dla elektronów może więc przyjmować wartości
dla elektronów może więc przyjmować wartości  .
Wartości j dla elektronów równe są wiec:
.
Wartości j dla elektronów równe są wiec: 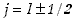 .
Jedynie dla l=0 mamy j=1/2.
.
Jedynie dla l=0 mamy j=1/2.
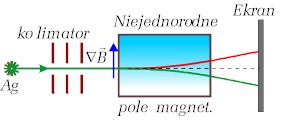
![]() oznaczone jest źródło emisji atomów srebra a
oznaczone jest źródło emisji atomów srebra a ![]() oznacza kierunek zmiany pola magnetycznego. Symbolizuje to również
nasilający się ku górze kolor niebieski w obszarze pola. Wiązka była
neutralna więc rozumieli oni, że odchylenie może nastąpić jedynie
wskutek istnienia orbitalnego momentu magnetycznego.
oznacza kierunek zmiany pola magnetycznego. Symbolizuje to również
nasilający się ku górze kolor niebieski w obszarze pola. Wiązka była
neutralna więc rozumieli oni, że odchylenie może nastąpić jedynie
wskutek istnienia orbitalnego momentu magnetycznego.