Model atomu Bohra opisywał widmo atomu wodoru, czyli atomu posiadającego tylko jeden elektron. Próby opisu w ramach tego samego podejścia widma atomu helu o dwóch elektronach nie dały wyników zgodnych z obserwacjami doświadczalnymi. Nie było też możliwe określenie w ramach tego formalizmu względnego natężenia linii widmowych, można było jedynie określić ich położenie.

Zasadniczym jednak niedostatkiem modelu Bohra była jego wewnętrzna niespójność. Model zawiera elementy klasyczne i wprowadzone "ad hoc" elementy kwantowe; nie stanowi więc konsekwentnej teorii. Zaletą tego modelu było więc przede wszystkim uzmysłowienie potrzeby stworzenia nowej teorii, opartej na innych zasadach niż zasady fizyki klasycznej. Jak wiemy już, taką teorią jest mechanika kwantowa, której podstawowym równaniem jest równanie Schrödingera.

Zapiszmy równanie Schrödingera dla atomu wodoropodobnego, tzn. posiadającego jeden elektron. Ładunek jądra atomowego niech będzie +Ze. Kiedy Z=1, mamy do czynienia z atomem wodoru, kiedy jest większe, rozważamy zjonizowany atom czyli jon. Zagadnienie jest tu jednak znacznie bardziej skomplikowane w stosunku do rozważanego przez nas przypadku nieskończenie wysokiej studni potencjału. Po pierwsze potencjał nie ma ani nieskończonej, ani nawet stałej wartości w funkcji położenia. Energia potencjalna elektronu w polu dodatnio naładowanego jądra wyrażona jest, jak pamiętamy, wzorem analogicznym do wzoru (2.3.7).

(13.3.1)

(Znak minus jest rezultatem ujemnego znaku elektronu w polu dodatnio naładowanego jądra, kiedy mamy do czynienia z siła przyciągającą.)

Po drugie, mamy tu do czynienia z przypadkiem trójwymiarowym, a więc równanie Schrödingera musi być sformułowane w postaci wzoru (12.3.12) z tym wszakże ułatwieniem, że możemy założyć iż energia potencjalna nie jest zależna od czasu. Równanie Schrödingera ma więc postać analogiczną do wzoru (12.3.25), ale zapisanego dla trzech wymiarów i energii potencjalnej wyrażonej wzorem (13.3.1)

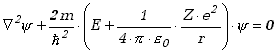(13.3.2)

Warto zauważyć, że układ nasz ma symetrię sferyczną. Energia potencjalna wyrażona wzorem (13.3.1) jest funkcją odległości od jądra. czyli w układzie współrzędnych prostokątnych zależy od wszystkich trzech współrzędnych. Uniemożliwia to rozseparowanie równania różniczkowego cząstkowego, jakim jest równanie (13.3.2), na układ równań różniczkowych zwyczajnych zależnych o poszczególnych współrzędnych (x,y,z). Wygodnie wiec będzie zapisać równanie Schrödingera w układzie współrzędnych sferycznych , i poszukiwać funkcji własnych w postaci iloczynu trzech funkcji zależnych oddzielnie od poszczególnych składowych. Podobnie uczyniliśmy już z równaniem (12.3.19), kiedy potencjał nie zależał od czasu i równanie to rozseparowaliśmy na dwie części; jedną zależną tylko od czasu i drugą, od położenia.

Układ współrzędnych sferycznych zdefiniowaliśmy w lekcji drugiej kursu Fizyka I. Operator Laplace'a (12.3.11) ma w tym układzie następującą postać

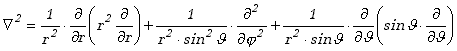(13.3.3)

Równanie Schrödingera zapisujemy więc w formie

(13.3.4)

Nie będziemy tu przytaczać szczegółów rozwiązywania tego równania. Wymaga ono wykonania szeregu kroków pośrednich i podstawień, zaś rozwiązania wyrażają się przez funkcje specjalne w postaci szeregów. Więcej szczegółów można znaleźć np. w pozycji 1 podanej bibliografii. Ważne jest, że funkcje własne tego równania mają postać iloczynu funkcji zależnych od poszczególnych współrzędnych w układzie sferycznym.

(13.3.5)

Występujące tu parametry: n, l, m noszą nazwę liczb kwantowych odpowiednio: głównej, orbitalnej lub azymutalnej i magnetycznej. Liczby te przybierać mogą wartości:

	główna liczba kwantowa:
	orbitalna liczba kwantowa:			(13.3.6)
	magnetyczna liczba kwantowa:

Liczby te (i warunki na ich możliwe wartości) pojawiają się jako indeksy numerujące poszczególne, dopuszczalne matematyczne rozwiązania równania (13.3.4). Jak zobaczymy niżej, pojawiają się one w wyrażeniach na fizyczne wielkości określające stan kwantowy elektronu w atomie, kwantując ich wartości. W ten sposób ze zwykłych indeksów matematycznych stają się fizycznymi liczbami kwantowymi.

Główna liczba kwantowa określa energie stanów związanych elektronu w atomie wodoropodobnym. Energie te mają wartości ujemne i wynoszą

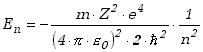(1.3.7)

Jest to dokładnie to samo wyrażenie, które uzyskaliśmy na podstawie warunków kwantyzacji Bohra. Tu jednak, wyrażenie to otrzymuje się jako rezultat rozwiązania podstawowego równania mechaniki kwantowej, które równocześnie opisuje cały szereg innych zagadnień i nie wymaga dodatkowych założeń. Dodajmy, że możliwe są również rozwiązania równania (13.3.4) o dowolnych dodatnich wartościach energii. Odpowiada to przypadkowi rozproszenia elektronu, który najpierw przybliża się, a potem oddala od jądra atomowego, a także elektronowi uwolnionemu z wiązania w atomie po jego jonizacji, czyli elektronowi swobodnemu..

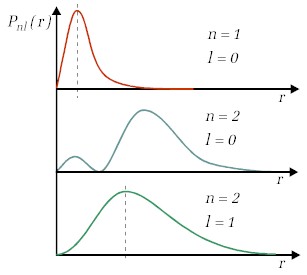Dodajmy również, że w wyniku rozwiązania równania (13.3.4) otrzymujemy także wyrażenia określające postać funkcji falowych, których kwadrat modułu, jak wiemy, wzór (12.3.15) pozwala określić prawdopodobieństwo znalezienia elektronu w danym obszarze przestrzennym. W przypadku ujemnych wartości energii, które odpowiadają stanom związanym elektronu, uzyskujemy rozkład prawdopodobieństwa znalezienia elektronu względem położenia jądra atomowego. Przykłady rozkładów w funkcji odległości od jądra (radialna gęstość prawdopodobieństwa) dla kilku pierwszych wartości n oraz l pokazuje Rys.13.3.1. Na rysunku tym linią przerywaną zaznaczone są położenia maksimów gęstości prawdopodobieństwa dla wartości l=l_max= n-1. Wartości r odpowiadające tym maksimom równe są wartościom promieni orbit elektronów określonych przez Bohra. Widzimy jednak, że zgodnie z mechaniką kwantową położenia te są "rozmyte"; nie są stałymi wartościami.

Rys.13.3.1. Gęstość prawdopodobieństwa znalezienia elektronów w funkcji odległości od jądra dla kilku wartości liczb n i l.

Zwróćmy uwagę na zasadniczą różnicę w podejściu klasycznym i kwantowym. Model Bohra przypominał układ planetarny z określonymi orbitami elektronów. W mechanice kwantowej nie ma żadnych orbit; jest rozkład prawdopodobieństwa. Trzeba jednak "oddać sprawiedliwość" Bohrowi, bo maksymalne gęstości prawdopodobieństwa wyznaczane przez mechanikę kwantową odpowiadają przewidzianym przez niego promieniom orbit. Elektron jednak wcale nie musi znajdować się w odległości od jądra równej promieniowi orbity Bohra. Najlepiej więc nie mówić o położeniu elektronu ale o rozkładzie prawdopodobieństwa położenia. Mówimy raczej o "chmurze elektronowej" wokół jądra, a nie o elektronie krążącym po orbicie

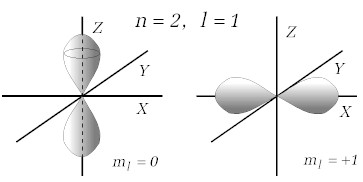
Gdy orbitalna liczba kwantowa l nie jest równa zeru, rozkład prawdopodobieństwa znalezienia elektronu w przestrzeni wokół jądra nie ma symetrii sferycznej. Przestrzenny rozkład prawdopodobieństw dla różnych kombinacji liczb kwantowych nosi nazwę orbitali. Rysunek 13.3.2 pokazuje dwa przykłady orbitali dla podanych tam kombinacji liczb kwantowych.

Rys.13.3.2. Przykłady orbitali dla n=2 i l=1.

Całkowita energia atomu, określona wzorem (13.3.7) zależy wyłącznie od głównej liczby kwantowej n. Funkcje własne są jednak zależne także od l i m_l. Oznacza to, że tej samej energii może odpowiadać kilka różnych stanów określonych różnymi wartościami tych liczb. Mówimy, że w takim przypadku funkcje własne są zdegenerowane, a takie stany atomu nazywamy zdegenerowanym lub zwyrodniałymi. Stopień lub krotność degeneracji ze względu na daną liczbę kwantową określa liczba stanów własnych odpowiadających danej wartości tej liczby. Liczba stanów odpowiadających tej samej wartości liczby n równa jest n stanom liczny kwantowej l mnożonym przez (2l+1) stanów liczmy kwantowej m_l czyli jest to suma postaci

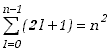(1.3.8)

Mówimy, że krotność degeneracji poziomów energetycznych wynosi w tym przypadku n². Stany o różnych wartościach orbitalnej liczby kwantowej mają tę samą energię ale różnią się wartością momentu pędu. Stanom tym przyporządkujemy symbole literowe,

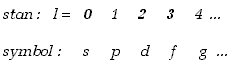(1.3.9)