Z przedstawionych faktów widać, że w świecie atomów istnieją bardzo wyraźne reguły, ale nie odpowiadają one regułom, którymi kieruje się fizyka klasyczna. W 1913 roku duński fizyk Niels Bohr zaproponował model atomu, który wprawdzie naruszał zasady fizyki klasycznej ale, ... opisywał wyniki doświadczeń. Punktem wyjścia było klasyczne założenie, że elektron porusza się w atomie po kołowej orbicie wskutek przyciągania elektrostatycznego przez dodatnio naładowane jądro atomowe. Przyjął też nieznane w fizyce klasycznej założenia zwane dziś postulatami Bohra:

  1. Elektron w atomie może poruszać się tylko po takich orbitach, dla  których orbitalny moment pędu równy jest całkowitej wielokrotności stałej Plancka . W takim stanie ruchu elektron nie emituje promieniowania elektromagnetycznego.
  2. Emisja promieniowania następuje w sposób nieciągły gdy elektron zmienia swe położenie przeskakując na inna orbitę. Częstotliwość wyemitowanego wówczas promieniowania określona jest przez  różnicę energii elektronu na obu orbitach:  gdzie E1 i E2 oznaczają odpowiednio energie elektronu na orbitach przed i po emisji.

Oczywiście, postulaty Bohra pozostają w ścisłej relacji z postulatami Plancka i Einsteina, ale odnoszą się bezpośrednio do budowy atomu. Kwantowanie emisji (Planck) czy  absorpcji (Einstein) promieniowania jest tu naturalna konsekwencją postulatów Bohra dotyczących struktury atomu.

Zastosujmy postulaty Bohra do atomu o składającego się z jądra o masie M i ładunku +Ze oraz jednego elektronu o masie m i ładunku -e. Liczbę Z nazywamy liczbą atomową. Zwróćmy uwagę, że model taki dotyczy atomu wodoru lub atomów "wodoropodobnych": tj. jonów z jednym tylko elektronem. Używając terminu "atom" będziemy więc tu rozumieć atom wodoropodobny. Warunek krążenia elektronu z prędkością  na orbicie o numerze n, która ma promień  rn sprowadza się do równości siły przyciągania elektrostatycznego i siły odśrodkowej,

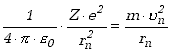. (13.2.1)

 Z pierwszego postulatu Bohra wynika, że

. (13.2.2)

Podstawiając wyrażenie na prędkość wzięte ze wzoru (13.2.2) do wzoru (13.2.1) otrzymujemy wzory określające promień n-tej orbity stacjonarnej elektronu, oraz prędkość elektronu na tej orbicie

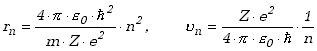(13.2.3)

Na energię atomu składa się energia kinetyczna elektronu na orbicie i energia potencjalna jego wiązania. (Zakładamy, że jądro atomowe jest nieruchome.) 

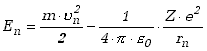(13.2.4)

Wykorzystując związek (13.2.1) możemy zapisać inaczej wyrażenie (13.2.4) 

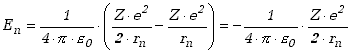(13.2.5)

Promień n-tej orbity rn mamy już wyliczony, wzór (13.2.3). Wykorzystując to możemy zapisać wyrażenie na energię elektronu w postaci 

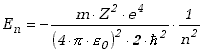(13.2.6)

Kiedy elektron przechodzi ze stanu n do stanu m, wypromieniowując zgodnie z drugim postulatem Bohra energię to różnica energii atomu wynosi

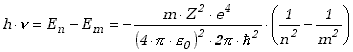(13.2.7)

Odpowiadająca tej różnicy energii częstotliwość fali wynosi

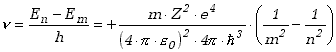(13.2.8)

(Zwracamy uwagę na zmianę kolejności wyrażeń w nawiasie po prawej stronie i związaną z tym zmianą znaku.) Liczba falowa (wzór 13.1.2) odpowiadająca temu przejściu wyrazi się wzorem

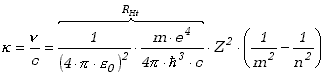(13.2.9)

Otrzymaliśmy wzór analogiczny do wzoru na serie widmowe atomu wodoru (13.1.5), jeśli przyjmiemy, że Z=1 (co odpowiada ładunkowi jądra atomu wodoru). Teraz jednak nie jest to już zwykłe zauważenie prawidłowości w danych pomiarowych, ale rezultat określonego założenia teoretycznego. Co więcej, na podstawie tego wzoru mamy wyznaczoną wartość stałej Rydberga, którą tu oznaczyliśmy przez RHt. Wartość tej stałej bardzo dobrze zgadza się z wartością wyznaczoną doświadczalnie. Jest to niewątpliwy sukces modelu atomu Bohra.