Kiedy podgrzewamy kawałek pręta metalowego np. w ogniu kuchenki gazowej, zauważamy, że już po chwili pręt staje się ciepły, następnie gorący, następnie zaś zaczyna świecić początkowo światłem czerwonym, potem coraz bardziej zbliżonym do światła białego. Na tym zwykle kończy się eksperyment tego typu w warunkach domowych. Emisja ciepła przez pręt zauważalna jest po zbliżeniu ręki (byle się nie sparzyć), emitowane światło odbierane jest naszym wzrokiem. Mówimy, że rozgrzany pręt emituje promieniowanie cieplne i promieniowanie świetlne. Wiemy, że oba rodzaje promieniowania stanowią fale elektromagnetyczne różniące się długością, a w konsekwencji są różnie odbierane przez nasze zmysły. Natura obu rodzajów promieniowania jest jednak taka sama. Wiemy też, że zakres rejestrowanych długości fal elektromagnetycznych w ogólności  wykracza daleko w obie strony poza obszary promieniowania cieplnego i świetlnego. (Zobacz wstęp do lekcji dziesiątej, gdzie pokazane jest widmo promieniowania elektromagnetycznego z podziałem na wiele zakresów.)

Biorąc pod uwagę umiejscowienie promieniowania cieplnego w zakresie podczerwieni i świetlnego w zakresie mniejszych długości fal (większych częstotliwości) wyciągamy wniosek, że wyższym temperaturom odpowiadają  większe częstotliwości, czyli mniejsze długości fal. Pamiętamy z kursu Fizyka I, że temperatura jest miarą średniej energii kinetycznej cząsteczek, zaś rozkład tych energii związany jest bezpośrednio z rozkładem prędkości cząsteczek (omawianym w lekcji dwunastej tego kursu) i opisanym przez funkcję rozkładu Maxwella. Wiemy, że kształt tego rozkładu zależy od wartości temperatury. Nie dziwi nas więc, że "rozgrzany do czerwoności" pręt zarówno świeci jak i grzeje, czyli wysyła fale elektromagnetyczne z szerokiego zakresu długości fal. Przyjmując, że fale elektromagnetyczne emitowane są  przez drgające wskutek pobudzenia termicznego ładunki elektryczne, możemy intuicyjnie zrozumieć zarówno proces emisji promieniowania jak i jego absorpcji, kiedy padające na ciało promieniowanie pobudza ładunki do drgań, w rezultacie czego jest absorbowane. 

To, że widzimy pręt metalowy zanim zacznie świecić wynika z faktu, że chociaż część światła jest przez pręt absorbowana, to pozostała część odbija się i trafia do naszego oka. Przedmiot jest ciemny, jeśli absorbuje dużą część światła. Jeśli ciało absorbuje całe padające nań światło niezależnie od częstotliwości, to nazywamy go ciałem doskonale czarnym. Wszystkie ciała doskonale czarne emitują promieniowanie o takim samym widmie, czyli  takim samym rozkładzie prawdopodobieństwa rożnych długości fal. Ta ważna właściwość  sprawiła, że widmo promieniowania ciał doskonale czarnych próbowano opisać na gruncie klasycznych własności fal elektromagnetycznych. 

Oznaczymy przez wielkość charakteryzującą zdolność emisyjną ciała doskonale czarnego w ten sposób, że wyrażenie równe jest energii promieniowania o częstotliwościach z przedziału od do emitowanego w ciągu jednostki czasu przez jednostkę powierzchni ciała o temperaturze . Całka z tak zdefiniowanej wielkości po wszystkich częstotliwościach równa jest całkowitej energii emitowanej przez jednostkę powierzchni tego ciała w jednostce czasu  

	Kiedy temperatura rośnie, rośnie również całkowita energia , a częstotliwość przy której osiąga wartość maksymalną przesuwa się ku większym wartościom. Jest to treścią tzw. prawa przesunięć Wiena, według którego  . Ilustruje to rysunek 11.1.1. Zamieniając częstotliwość długością fali (pamiętamy, że dla próżni ) otrzymujemy
		(11.1.2)
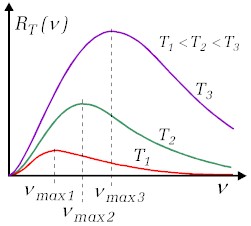
Rys.11.1.1. Ilustracja prawa przesunięć Wiena

 Z kolei, zależność całkowitej energii od temperatury opisuje prawo Stefana-Boltzmanna, stwierdzone empirycznie przez Stefana i wyprowadzone na gruncie zasad termodynamiki przez Boltzmanna, według którego 

gdzie jest stałą Stefana-Boltzmanna.

Te empiryczne prawidłowości opisują niektóre własności emisji promieniowania termicznego, ale nie tłumaczą mechanizmu tej emisji. Dla zrozumienia tych mechanizmów rozpatrzmy pewien model ciała doskonale czarnego.

Rayleigh i Jeans wykonali obliczenia umożliwiające wyznaczenie rozkładu widmowego tego promieniowania. Obliczenia ich dotyczyły rozkładu  gęstości energii  promieniowania pozostającego wewnątrz wnęki w równowadze termicznej. Gęstość energii określona jest jako energia zawarta w jednostce objętości wnęki przy zadanej temperaturze T,  w przedziale częstotliwości od do . Wydostające się promieniowanie ma taki sam rozkład częstotliwości tzn. . Ich obliczenia opierały się na znanej nam już klasycznej teorii promieniowania elektromagnetycznego. Założyli oni, że wewnątrz wnęki wytwarza się układ stojących fal elektromagnetycznych. Liczba fal z danego przedziału częstotliwości (lub długości fal) określona jest przez warunki geometryczne położenia węzłów fal stojących na ściankach wnęki, zaś energia fal zależna jest od temperatury (zakładając warunki równowagi termicznej).  Przyjęli, że średnia energia fali stojącej jest niezależna od częstotliwości i wynosi , co jest zgodne ze znaną z termodynamiki zasadą ekwipartycji energii. (Zwracamy na to założenie szczególną uwagę, jest to bowiem podstawowy element  ich rozumowania.) Mnożąc liczbę fal z danego przedziału częstotliwości przez średnią energię i dzieląc przez objętość wnęki można określić gęstość energii w funkcji częstotliwości czyli . Więcej szczegółów dotyczących ich obliczeń można znaleźć w pozycjach: 1-3 podanej bibliografii. W rezultacie otrzymuje się wzór, zwany wzorem Rayleigha- Jeansa.

gdzie k jest znaną z termodynamiki stałą Boltzmanna. Zauważmy, że wzór ten stanowi iloczyn średniej energii, , pomnożonej przez czynnik określający prawdopodobieństwo występowania danej częstotliwości w widmie promieniowania. Występujący w nim kwadrat częstotliwości jest prostą konsekwencją wyrażania elementu objętości we współrzędnych sferycznych (). Czynnik ten jest więc proporcjonalny do powierzchni warstwy kulistej określonej przez kwadrat częstotliwości  , pomnożonej przez "grubość" warstwy, . 

Całkowitą gęstość energii promieniowania obliczymy stosując wzór analogiczny do wzoru (11.1.1)

Otrzymany wynik jest w jawnej sprzeczności z eksperymentem, gdzie zdolność emisyjna ciał jest wprawdzie bardzo silnie rosnącą funkcją temperatury, zgodnie z prawem Stefana-Boltzmanna, ale ma wartości skończone.

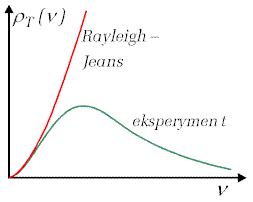Rysunek 11.1.3. przedstawia schematyczne porównanie rozkładu wynikającego ze wzoru Rayleigha-Jeansa z kształtem rozkładu doświadczalnego. W zakresie małych częstotliwości (stosunkowo dużych długości fal) rozkład dobrze opisuje dane doświadczalne, ale dla wyższych częstotliwości rozbieżność jest ... katastrofalna. Rzeczywiście, tak ogromną rozbieżność nazwano katastrofą nadfioletu bo okazało się, że właśnie w tym zakresie fal pojawia się niezgodność przewidywań klasycznej teorii promieniowania elektromagnetycznego z wynikami doświadczenia.

Rys.11.1.3.  "Katastrofa nadfioletu"

Krzywa teoretyczna (koloru czerwonego na rysunku) ze wzrostem częstotliwości zdąża do nieskończoności , podczas gdy dane doświadczalne (kolor zielony) wykazują odwrotną tendencję. Niezgodność ta zburzyła poczucie pewności, panujące w końcu XIX wieku, o rozwiązaniu wszelkich problemów współczesnej (ówczesnej) fizyki.