Kiedy mija nas karetka pogotowia jadąca "na sygnale" zauważamy, że wysokość sygnału dźwiękowego nagle zmniejsza się - sygnał staje się "niższy", kiedy karetka zaczyna się od nas oddalać.  Zjawisko to zwane jest efektem Dopplera i obserwowane jest nie tylko dla fali dźwiękowej, ale także dla fal elektromagnetycznych. Najpierw omówimy mechanizm tego zjawiska na przykładzie podłużnej fali dźwiękowej.

Kiedy fala dźwiękowa o długości rozchodzi się z prędkością , a my nie poruszamy się względem źródła, to w czasie t dociera do nas fal. Odpowiada to częstotliwości dźwięku , wzór (9.1.8), . Kiedy zbliżamy się  źródła dźwięku z prędkością , to dodatkowo dociera do nas jeszcze   fal. Odpowiada to częstotliwości

(10.5.1)

Wykorzystując znów związek (9.1.8) otrzymujemy

(10.5.2a)

Kiedy oddalamy się od źródła dźwięku to zmniejsza się liczba fal docierających do nas w danym czasie i ton słyszanego dźwięku jest niższy;  mamy bowiem

(10.5.2b)

Kiedy my się nie poruszamy ale porusza się źródło dźwięku (np. zbliżająca się karetka), to obrazowo możemy powiedzieć, że źródło (karetka) stara się dogonić uciekającą falę. W czasie jednego okresu fala przesunie się o odcinek ale źródło przesunie się o odcinek . Długość fali będzie więc zmniejszona o odcinek jaki przebywa źródło w czasie jednego okresu

(10.5.3)

Mniejsza długość fali odpowiada większej częstotliwości dźwięku, jak wynika ze związku (9.1.8). Częstotliwość docierającej do nas fali dźwiękowej będzie wiec

(10.5.4a)

 Kiedy źródło dźwięku się oddala, to ton dźwięku staje się niższy. W czasie jednego okresu źródło oddala się od nas o odcinek równy i o tyle powiększona jest długość fali. Rozumując analogicznie jak w przypadku zbliżania się źródła dźwięku otrzymujemy wyrażenie na częstotliwość fali docierającej do nas od oddalającego się źródła.

(10.5.4b)

Z postaci wyrażenia po prawej stronie wzoru (10.5.4a) widać, że kiedy prędkość źródła będzie zbliżać się do prędkości fali, to częstotliwość będzie dążyć do nieskończoności, a kiedy będzie większa, to całe wyrażenie traci sens fizyczny. W takich przypadkach nie można stosować podanych wyżej wzorów na zmianę częstotliwości, bowiem sama fala zmienia się w czasie, a jej kształt jest inny. Dla prędkości większych od prędkości fazowej fali w danych ośrodku występuje zjawisko fali uderzeniowej, które ma miejsce kiedy samoloty poruszają się z prędkością większą od prędkości dźwięku w powietrzu.

Zmiana częstotliwości w wyniku efektu Dopplera dla fal elektromagnetycznych (a więc i światła) w odniesieniu do sytuacji omówionych wyżej, opisana jest jednak innymi wzorami (przy tym samym znaku zmiany częstotliwości). Wynika to z różnej natury fali elektromagnetycznej i fali dźwiękowej oraz różnej roli ośrodka, w którym rozchodzą się fale. Fala dźwiękowa jest falą polegającą na rozchodzeniu się sprężystych odkształceń samego ośrodka materialnego (nie może się więc rozchodzić w próżni), zaś fala elektromagnetyczna polega  na rozchodzeniu się zaburzeń pola elektrycznego i magnetycznego, które to zaburzenia mogą rozchodzić się w dowolnym ośrodku (także w próżni i to z jednakową zawsze maksymalną prędkością  c). 

Rozpatrując, jak powyżej dla akustycznego efektu Dopplera, wpływ ruchu obserwatora bądź źródła fali elektromagnetycznej (np. światła) z zastosowaniem właściwej dla prędkości relatywistycznych transformacji współrzędnych położenia i czasu (tj. transformacji Lorentza)  otrzymujemy dla przypadku obserwatora poruszającego się z prędkością i nieruchomego źródła wzór na częstotliwość fali odbieranej

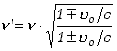(10.5.5)

gdzie górne znaki odpowiadają oddalaniu się obserwatora od źródła (dając ), a dolne - zbliżaniu (dając ).

Dla przypadku źródła poruszającego się z prędkością  i nieruchomego obserwatora

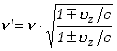(10.5.6)

gdzie przyporządkowanie znaków związane jest ze względnym oddalaniem i zbliżaniem się źródła i obserwatora tak jak wyżej.