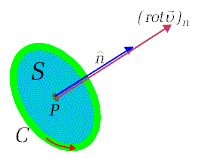
Zauważamy, że tak zdefiniowana wielkość zależy od rozmiarów konturu oraz od jego orientacji względem kierunku wektora prędkości. W ogólnym przypadku rurka może mieć dowolny kształt a pole wektora prędkości może być skomplikowaną funkcją położenia. Na rysunku 1.6.1 pokazany jest przykładowy kontur ograniczający powierzchnię wokół punktu . Kiedy jednak powierzchnia ta będzie się kurczyć czyli będzie zdążać do zera, a wartość cyrkulacji po konturze podzielimy przez , to określimy wielkość stanowiącą charakterystykę pola w danym punkcie i niezależną od wielkości powierzchni.  

Pozostaje jeszcze do zdefiniowania orientacja tej powierzchni względem kierunku prędkości. Wybieramy taką orientację w której cyrkulacja będzie maksymalna przy zdążającej do zera powierzchni. Podobnie jak w przypadku definicji strumienia, orientację tę zdefiniujemy poprzez kierunek normalnej (czyli prostopadłej) do płaszczyzny konturu. Przyjmiemy też umowę, że obchodząc kontur przy wykonywaniu całkowania we wzorze (1.5.1) poruszać się będziemy wzdłuż kierunku normalnej określonym regułą śruby prawoskrętnej, co ilustruje rysunek 1.6.1.

Rys. 1.6.1. Kierunek wektora rotacji.

 Wielkość zdefiniowaną jako stosunek cyrkulacji danego wektora ( na przykład wektora prędkości ) do powierzchni wokół punktu ( patrz rysunek 1.6.1), która obejmowana jest przez kontur gdzie cyrkulacja się odbywa - nazywamy rotacją  lub wirowością  albo też wirem wektora w punkcie . 

 Indeks "n" podkreśla, że zdefiniowana tu rotacja wektora ma charakter kierunkowy i w tym przypadku związana jest z kierunkiem normalnej do powierzchni S rozpiętej na konturze C. Rotacja wektora jest więc także wektorem.

Rozważanie nasze przeprowadziliśmy dla wektora prędkości, bowiem ułatwiło to nam poglądowe przedstawienie wielkości, którymi posługujemy się dla zdefiniowania wektora rotacji. W ten sam jednak sposób możemy zdefiniować wektor rotacji dla dowolnego pola wektorowego.

Nietrudno zapisać rotację w układzie współrzędnych prostokątnych. W tym celu wyznaczmy składowe rotacji dla kierunków pokrywających się z kierunkami osi układu współrzędnych. Dla wyznaczenia składowej  przyjmijmy, że normalna pokrywa się z osią , czyli kontur leży w płaszczyźnie . Powtarzając tę operację dla pozostałych składowych wyznaczymy wszystkie składowe, czyli wyrazimy wektor rotacji w układzie współrzędnych prostokątnych. 

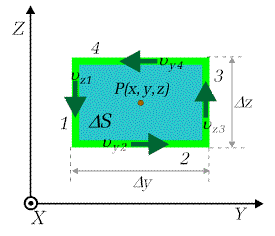Rysunek 1.6.2 ilustruje przypadek dla składowej .  Dla uproszczenia zakładamy, ze kontur ma kształt prostokąta o bokach i . Oś jest skierowana tak, że układ jest prawoskrętny. Strzałkami ciemnozielonymi pokazane są kierunki prędkości na poszczególnych odcinkach. Zgodnie z oznaczeniami na rysunku i definicją (1.5.1) cyrkulację zapiszemy jako sumę iloczynów średnich prędkości w poszczególnych odcinkach prostokąta przez odpowiadające długości boków. Uwzględnimy przy tym w postaci ujemnego znaku, że kierunki prędkości na odcinkach  1 i 4 są odwrotne niż odpowiadające im  kierunki osi współrzędnych. W rezultacie otrzymujemy wyrażenie

Rys.1.6.2. Cyrkulacja w płaszczyźnie (Y,Z)

Podobnie jak przy wyznaczaniu strumienia, wyrazimy przyrosty prędkości na odcinku przez i na odcinku przez tj. poprzez iloczyny pochodnych cząstkowych w środku tego obszaru czyli w punkcie P  przez  odpowiadające przyrosty współrzędnych (zobacz też wzór (1.1.14)). W rezultacie możemy cyrkulację w punkcie P zapisać w postaci

gdzie jest powierzchnią ograniczającą kontur w płaszczyźnie . Dzieląc wyrażenie (1.6.3)  przez wyznaczamy rzut wektora na oś , czyli składową tego wektora. 

W analogiczny sposób wyznaczamy rzuty na dwie pozostałe osie. Pamiętać przy tym należy, by zachowywać zawsze układ prawoskrętny.  Ostatecznie, wektor rotacji we współrzędnych prostokątnych zapisujemy w postaci.

Operator rotacji działając na wektor daje więc nowy wektor. Składowe tego wektora są kombinacją przemienną pochodnych składowych wektora na który działa rotacja względem współrzędnych przestrzennych.

Pojęcie rotacji pola wektorowego może być dobrze zilustrowane za pomocą wspominanego już wiatraczka. Wykonajmy w naszym domowym laboratorium proste doświadczenie używając wyłącznie łatwo dostępnych materiałów. (Jak widać na zdjęciu poniżej, użyliśmy tu: suszarki do włosów, linijki, kawałka kartonu i drutu oraz taśmy samoprzylepnej; nie ma tu skomplikowanej (i drogiej) aparatury...)

Nauczanie przez działanie
	Wykonaj proste doświadczenie ilustrujące składowe wektora rotacji, we współrzędnych prostokątnych Dmuchawa (np. suszarka do włosów) kieruje strumień powietrza (strzałki czerwone) w stronę małego wiatraczka  umieszczanego na drucie przymocowanym do ściany. Na drucie tym zawieszona jest też cienka blaszka, która może odchylać się (strzałka zielona) pod wpływem strumienia powietrza.  Dmuchawa przesuwa się w dół (strzałka niebieska).
Odpowiedz: 1. W jakim położeniu dmuchawy wiatraczek będzie się obracać, a w jakim nie ? 2. Jeżeli będzie się obracać, to w jakim kierunku ? 3. Które i kiedy pochodne we wzorze (1.6.4) mają tu  niezerowe wartości ? 4. Jaki jest znak pochodnych o niezerowych wartościach ? 5. Które z pochodnych zachowują przez cały czas wartości bliskie zeru ? 6. Rozpatrz trzy przypadki: dmuchawa w położeniu: a-górnym, b-środkowym i c-dolnym. 7. Wykonaj tabelę dla trzech w/w przypadków i wszystkich sześciu pochodnych. 8. Oznacz odpowiednio: -1, 0, +1  -  pochodna: mniejsza od zera, bliska zeru, większa od zera. 9 Wykonaj tabelę dla trzech w/w przypadków i wszystkich sześciu pochodnych. 10. Jeśli masz już odpowiedzi - sprawdź ich poprawność klikając w polu obrazka ! Nie zapomnij przesłać do swego opiekuna tabeli z pochodnymi oraz uwagi własne.