
WARSAW UNIVERSITY OF TECHNOLOGY
INSTITUTE OF PHYSICS
ECOLE DES MINES DE NANTES
J. Pluta1), B. Pluta2), E. Peyre3), A. Wasążnik4), Z.J.-Szmek5)
WARSZAWA
1997
Pomiar jest podstawowym źródłem informacji w naukach przyrodniczych i technice. Proces pomiaru polega na porównaniu wielkości mierzonego obiektu z wzorcem przyjętym za jednostkę. Wynik pomiaru zawiera zasadniczo dwie informacje: wymiar jednostki (np. metr, sekunda, kilogram, amper itp.) oraz wartość liczbową, która określa ile razy mierzony obiekt jest większy lub mniejszy od przyjętego wzorca.
Uzyskana w wyniku pomiaru liczba będąca wynikiem pomiaru nie jest jednak nigdy wyznaczona bezwzględnie precyzyjnie. Dlatego rezultat pomiaru musi zawsze zawierać informację określającą dokładność uzyskanej wartości liczbowej. Bez tej dodatkowej informacji wynik pomiaru może prowadzić do zupełnie .
W przedstawionym tu modelowaniu komputerowym pokazane zostaną mechanizmy powstawania błędów pomiarowych, metody oszacowania dokładności pomiarów oraz interpretacja statystyczna wyznaczonych wartości reprezentujących wynik pomiaru i jego dokładność.
Błędy występujące w pomiarach można podzielić na trzy grupy, które określają też sposób w jaki powinny być one traktowane w procesie pomiaru.
Błędy, których wyeliminowanie nie jest możliwe, noszą też nazwę niepewności pomiarowych.
Charakterystyczną cechą błędów przypadkowych jest to, że na błąd pomiaru składa się suma wielu małych, niezależnych przyczynków, tzw. błędów elementarnych. Spowodowane są one czynnikami wynikającymi z zewnętrznych warunków prowadzenia pomiarów (np. zmian temperatury), właściwości obiektu mierzonego (np. elastyczności materiału w pomiarach długości), niestabilnej pracy urządzeń pomiarowych, itp. W rezultacie, przy kilkakrotnym wykonywaniu pomiarów tej samej wielkości uzyskuje się różne wyniki. Wyniki te grupują się wokół wartości prawdziwej, zaś ich rozrzut może być miarą dokładności pomiaru. Samej wartości prawdziwej nie znamy, możemy jednak uzyskać jej wartość przybliżoną, oraz ocenić na ile wyznaczona wartość może różnić się od wartości prawdziwej.
Traktując błędy przypadkowe jako wartości zmiennej losowej, możemy dla naszych ocen zastosować pojęcia rachunku prawdopodobieństwa i statystyki matematycznej.
Przypomnijmy te, które dotyczą bezpośrednio naszego ćwiczenia.
Wartość oczekiwana lub wartość przeciętna E(x), zmiennej losowej x określona jest jako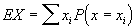 | (1) |
gdzie P(xi ) jest prawdopodobieństwem, że zmienną losowa x, będzie mieć wartość xi, a sumowanie rozciąga się na wszystkie możliwe wartości zmiennej losowej dyskretnej.
Dla zmiennych losowych o rozkładzie ciągłym wartość oczekiwana zdefiniowana jest jako
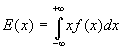 | (2) |
gdzie f(x) jest gęstością prawdopodobieństwa zmiennej losowej x.
Rozrzut wartości zmiennej losowej x, wokół wartości oczekiwanej, określony jest przez odchylenie standardowe s,
| s2(x)=E{[x-E(x)]2}=E(x2)-[E(x)]2 | (3) |
W rzeczywistych pomiarach nie znamy jednak ani wartości oczekiwanej ani odchylenia standardowego. Wykonujemy natomiast serię N pomiarów i wyliczamy wartość średnią,<x>,oznaczaną też jako 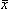 .
.
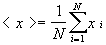 | (4) |
Rozrzut poszczególnych pomiarów wokół wartości średniej opisujemy z pomocą tzw. średniego błędu kwadratowego pojedynczego pomiaru, sx .
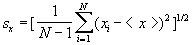 | (5) |
Dokładność wyznaczenia wartości średniej określamy poprzez tzw. średni błąd kwadratowy średniej:
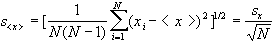 | (6) |
Wyznaczone w ten sposób wielkości <x> i sx zbiegają przy zdążającej do nieskończoności liczbie pomiarów do zdefiniowanych wcześniej wartości E(x) i s. Wielkość s<x> charakteryzuje odchylenie standardowe rozrzutu wartości średnich.
Taka procedura pozostawia jednak szereg otwartych kwestii; na przykład:
Można sformułować bardziej ogólne pytanie - co oznacza liczba nieskończenie wielka - w praktyce.
Celem przedstawionego tu eksperymentu komputerowego jest ułatwienie znalezienia odpowiedzi na postawione wyżej i podobne pytania poprzez analizę procesu pomiaru oraz mechanizmów prowadzących do powstawania błędów pomiarowych. W przeciwieństwie do realnych pomiarów, będziemy znać wartość prawdziwą x, stanowiącą punkt odniesienia w naszych rozważaniach. Będzie również możliwe wykonanie dużej liczby pomiarów w stosunkowo krótkim czasie.
Równocześnie zobaczymy, że proces powstawania błędów pomiarowych posiada wiele cech wspólnych dla całej klasy procesów statystycznych i wiedza zdobyta przy opisie procesu pomiaru może znaleźć zastosowanie w wielu dziedzinach życia, niekoniecznie dotyczących fizyki.
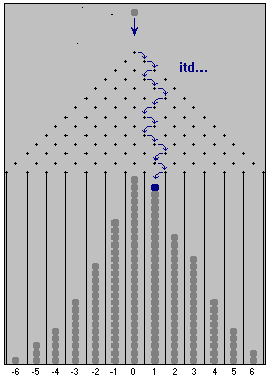
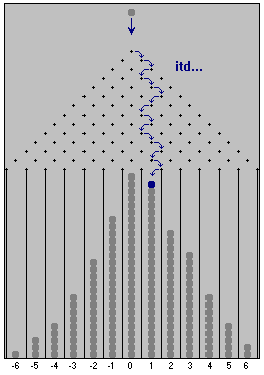
Poglądowym modelem ilustrującym proces pomiaru jest tzw. Tablica Galtona. W oryginalnym wykonaniu przyrząd ten stanowi płyta na której rozmieszczone jest wiele rzędów kołeczków, Rys. 1. Tablica ustawiona jest pionowo bądź nachylona względem pionu.
 |
 |
Po lewej - Ilustracja ruchu kulki na tablicy Galtona. Po prawej - mechaniczna wersja tablicy Galtona w Laboratorium studenckim Instytutu Fizyki PW, wykonana przez p. Andrzeja Kozłowskiego. |
Wykonujemy pomiar wielkości x, czyli spuszczamy kulkę na tablicy Galtona. Najmniejsza działka naszego przyrządu pomiarowego równa jest odległości między kołeczkami w rzędzie. Następujące relacje określają związki pomiędzy rzeczywistym i modelowanym pomiarem.
Sprecyzujmy podstawowe cechy procesu powstawania błędów przypadkowych oraz zestawmy je z własnościami ruchu kulek na tablicy Galtona (są to tzw.: założenia Hagena):
Oznaczmy przez ±d dwie możliwe wartości przemieszczenia kulki wskutek zderzenia z kołeczkiem, a przez p prawdopodobieństwo przemieszczenia w jedną (np. prawą) stronę. Prawdopodobieństwo przemieszczenia w lewo wyniesie oczywiście: q=1-p. Jeżeli spełnione jest trzecie założenie Hagena, to p=q=0.5. Zwróćmy też uwagę, że wielkość d równa jest połowie odstępu pomiędzy kołeczkami w rzędzie.
Procedura modelowania składa się z dwóch zasadniczych części:
Wykonanie analizy wyników modelowania wymaga zrozumienia szeregu zagadnień z zakresu statystycznej analizy danych. Niezbędne wiadomości podane są poniżej Następnie przedstawiony jest zestaw zadań umożliwiający powiązanie wiedzy teoretycznej z zastosowaniem jej w praktyce.
Niech nasza tablica Galtona posiada n poziomych rzędów kołeczków. Oznaczmy przez kliczbę przemieszczeń kulki w prawo nie interesując się w jakiej kolejności one zachodzą. Liczba kombinacji, w których kulka przemieści się k razy w prawo przy n rzędach kołeczków określona jest przez znany czynnik kombinatoryczny
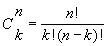 | (7) |
Zakładamy, że poszczególne przemieszczenia są wzajemnie niezależne, z czego wynika, że prawdopodobieństwo danej kombinacji przemieszczeń jest iloczynem prawdopodobieństw. Uzyskujemy wówczas bardzo prosty wzór określający prawdopodobieństwo tego, ze przy n rzędach kołeczków kulka przemieści się k razy w prawo.
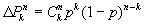 | (8) |
Jest to wzór opisujący tzw. dwumianowy rozkład prawdopodobieństwa. Wartość oczekiwana dla tego rozkładu wynosi: E(k)=np., zaś kwadrat odchylenia standardowego (wariancja), s2=np(1-p)=npq.
Przy k przemieszczeniach w prawo, które przyjmijmy za dodatnie, przemieszczenie sumaryczne kulki wyniesie
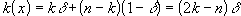 | (9) |
Kiedy więc k będzie równe n/2, czyli kulka odbije się tyle samo razy w prawo co i w lewo, przemieszczenie sumaryczne wyniesie zero - pomiar nasz będzie dokładny. Kiedy k będzie równe n lub zero, przemieszczenie będzie największe i wyniesie ± nd; to największy dla danej wartości n możliwy błąd pomiaru w naszej procedurze modelowania.
Opisując błędy przypadkowe zgodnie z założeniami Hagena zakładamy, że liczba błędów (przemieszczeń) jest bardzo duża, zaś poszczególne błędy (przemieszczenia) są bardzo małe. Aby to zrealizować w naszym modelu zwiększamy liczbę rzędów kołeczków zmniejszając równocześnie szerokość przegródki. Rozkład prawdopodobieństwa błędów pomiarowych (przemieszczeń) będziemy opisywać podając wartość stosunku DPkn/Dx gdzie Dx jest szerokością przegródki, która w naszym przypadku wynosi 2d
W granicy: n®¥, Dx®0, rozkład nasz przechodzi w krzywą ciągłą a zdefiniowany powyżej stosunek określa funkcje gęstości prawdopodobieństwa
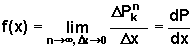 | (10) |
Analityczna postać tak otrzymanej krzywej stanowi treść jednego z fundamentalnych twierdzeń statystyki matematycznej, tzw. Centralnego Twierdzenia Granicznego. Sens tego twierdzenia wyrazić można następująco:
Jeżeli xi są niezależnymi zmiennymi losowymi podlegającymi rozkładowi o wartości przeciętnej a i odchyleniu standardowym s, to przy n®¥ ich suma podlega rozkładowi normalnemu (Gaussa) o wartości przeciętnej równej na i odchyleniu standardowym równym s*Ön.
Można pokazać, że sumy zmiennych losowych podlegają rozkładowi Gaussa nawet wówczas gdy nie wszystkie xi pochodzą z tego samego rozkładu. W naszym przypadku odpowiada to sytuacji, kiedy błędy elementarne mają różne wartości. Twierdzenie to ma ogromne znaczenie praktyczne, a dzięki niemu rozkład Gaussa należy do najbardziej rozpowszechnionych rozkładów statystycznych. Przykład wyprowadzenia rozkładu Gaussa poprzez wykonanie przejścia granicznego:
n®¥, Dx®, przy warunku nd2=const. (zwany metodą Hagena) podany jest w podręczniku Wróblewskiego i Zakrzewskiego, Wstęp do Fizyki, tom 1, str. 67.
Zmienna losowa x ma rozkład Gaussa, jeżeli jej gęstość prawdopodobieństwa zdefiniowana jest następująco:
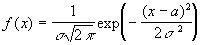 | (11) |
gdzie: a=E(x) jest wartością przeciętna, a s jest odchyleniem standardowym. Rozkład jest symetryczny względem wartości a, dla której gęstość prawdopodobieństwa osiąga maksimum. Parametr s określa "szerokość" rozkładu. Warto zapamiętać, że prawdopodobieństwo występowania zmiennej losowej w granicach jednego odchylenia standardowego względem wartości przeciętnej wynosi około 68.2 % zaś w granicach trzech wartości s wynosi 99.8 %.
Wiemy już dlaczego właśnie rozkład Gaussa stosujemy do opisu przypadkowych błędów pomiarowych. Pomimo jednak, że liczba rzędów kołeczków na tablicy jest duża a wielkość przegródki mała, zauważamy istotne różnice w wynikach modelowania w zależności od liczby wykonanych pomiarów.
Co więcej, nawet przy tej samej liczbie pomiarów, wyniki poszczególnych serii różnią się między sobą. Jest to naturalną konsekwencją faktu, że wykonując serię N pomiarów pobieramy próbę o wymiarze N, która ma reprezentować całą populację czyli zbiór wszystkich możliwych pomiarów wielkości mierzonej. Każdy wykonany pomiar jest próbą o wymiarze jeden.
Wielkości <x>, Sx, S<x>, podobnie jak wynik pojedynczego pomiaru, są także zmiennymi losowymi w odróżnieniu od ściśle określonych wartości parametrów rozkładu Gaussa. Wielkości te noszą nazwę estymatorów - odpowiednio: wartości oczekiwanej, odchylenia standardowego, odchylenia standardowego wartości średniej dla serii N pomiarów. Wartości estymatorów dążą do wartości estymowanych parametrów przy zdążającej do nieskończoności liczbie prób.
Kiedy jednak liczba pomiarów jest niewielka, liczby trafień do poszczególnych przegródek nie układają się w spodziewany regularny kształt. Łatwo jest to zaobserwować wykonując kilka serii po N pomiarów i obserwując zmieniające się liczby trafień do tej samej przegródki.
Trafienie kulki do danej przegródki możemy traktować jako jedną z n+1 możliwych wartości zmiennej losowej stanowiącej wynik naszego modelowanego pomiaru. Liczby trafień do poszczególnych przegródek przy N wykonanych pomiarach podlegać będą tzw. rozkładowi wielomianowemu będącego uogólnieniem rozkładu dwumianowego. Pomiędzy liczbami trafień do różnych przegródek wystąpi ujemna korelacja, bowiem kiedy kulka trafia więcej razy do jednej przegródki, to automatycznie musi mniej razy trafić do innych.
Kiedy liczba rzędów kołeczków jest bardzo duża wówczas korelacja ta staje się nieistotna i proces zapełniania przegródek możemy opisać rozkładem dwumianowym traktując trafienie do danej przegródki jako sukces zaś nie trafienie jako porażkę. Oczywiście, wartość p=DPkn mm będzie wówczas bardzo mała ale wartość oczekiwana takiego rozkładu będzie mieć nadal wartość skończoną równą Np, gdzie N jest liczbą wykonanych pomiarów.
Ten graniczny przypadek rozkładu dwumianowego, kiedy p zdąża do zera, a N zmierza do nieskończoności, ale tak, że iloczyn Np pozostaje stały, to także jeden z najważniejszych rozkładów statystycznych - rozkład Poissona. Inne przykłady tego rozkładu to: liczba aktów rozpadu substancji promieniotwórczej w ustalonym odcinku czasu, liczba gwiazd w określonym wycinku sfery niebieskiej, liczba klientów wchodzących do sklepu w danym odcinku czasu, itp.
Rozkład Poissona, podobnie jak i rozkład dwumianowy, określony, jest dla dyskretnej zmiennej losowej;
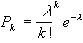 | (12) |
Jedynym parametrem rozkładu Poissona jest wartość oczekiwana, l
=np. Kwadrat odchylenia standardowego (wariancja) równa jest wartości oczekiwanej, s2=l.
Zwróćmy uwagę, że wartość stosunku s/l = 1/Öl
zmniejsza się za wzrostem wartości oczekiwanej. Oznacza to, że błąd względny związany ze statystycznym charakterem naszego procesu maleje wraz ze wzrostem liczby pomiarów i ilościowo może być opisany przez pierwiastek kwadratowy z liczby trafień do danej przegródki.
Konsekwencją omawianych wyżej fluktuacji statystycznych jest "poszarpany" kształt rozkładu wyników pomiarów, wizualnie niezgodny z gładkim rozkładem Gaussa. Wizualna niezgodność może być jednak uzasadniona dużą niepewnością statystyczną pomiarów. Istnieje więc potrzeba obiektywnego testu hipotezy zgodności wyników z rozkładem teoretycznym. Do tego celu wykorzystać można test zgodności c2.
W celu wykonania tego testu dzielimy wyniki uzyskanej serii pomiarów na M grup i wyznaczamy wartość wyrażenia
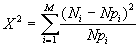 | (13) |
Każdy składnik w liczniku, to kwadrat różnicy pomiędzy liczbą pomiarów w danej grupie, a analogiczną liczbą przewidywana przez testowany rozkład statystyczny. w naszym przypadku grupę może stanowić zawartość jednej lub kilku przegródek. Jeżeli różnice te spowodowane są tylko przez rozrzut statystyczny, czyli nasza hipoteza jest prawdziwa, każdy składnik sumy powinien być rzędu jedynki (por. stosunek s2/l, powyżej). Wartość X2 będzie więc rzędu M, a jej rozkład będzie zgodny z rozkładem c2. Jedynym parametrem tego rozkładu jest liczba stopni swobody, NDF=(M-L-1); L jest liczba parametrów testowanego rozkładu, np. 2 - dla rozkładu Gaussa, 1 - dla rozkładu Poissona. Dla weryfikacji naszej hipotezy należy wprowadzić jeszcze tzw. poziom ufności, a. Jeżeli wartość X2 jest większa niż c2 dla danych NDF i a, to hipotezę należy odrzucić.
Ważnym elementem testu c2 jest wybór szerokości przedziałów, które powinny być na tyle wąskie, by odzwierciedlać kształt badanego rozkładu, ale i na tyle szerokie, by zapewnić w każdej grupie wystarczającą liczbę obserwacji przewidywanych przez testowany rozkład. Liczbę 5 przyjmuje się zwykle jako wystarczającą. Jest to szczególnie ważne na brzegach rozkładów, gdzie liczby obserwacji często są niewielkie. Właśnie wówczas można wziąć sumę obserwacji z kilku przedziałów jako jedną grupę.
Poniżej przedstawionych jest kilka przykładów analizy rezultatów modelowania, które należy wykonać w ramach tego ćwiczenia. Podany zestaw nie wyczerpuje oczywiście istniejących możliwości. Wykonanie również innych testów traktowane będzie jako twórczy wkład w zrozumienie praw statystyki leżących u podstaw analizy danych doświadczalnych.
Uwaga: Wyniki należy przedstawić w postaci liczbowej i graficznej. Należy podać również wynikające z analizy wnioski.
Prawidłowo wykonany pomiar powiększa zasób naszej wiedzy i umożliwia wyciagnięcie właściwych wniosków: naukowych, ekonomicznych, sportowych, socjologicznych itd. W przypisie na stronie pierwszej podano przykład błędnego wniosku spowodowanego zignorowaniem skali niepewności uzyskanej informacji. Konkretne wnioski zależne są od badanego problemu, jednak zawsze przy wyciąganiu wniosków musi być wzięta pod uwagę niepewność uzyskanej informacji, niezależnie od dziedziny, której ona dotyczy.
Uwaga ta odnosi się także do pomiaru, jakim było przestudiowanie tego opracowania. Z cała pewnością zawarte powyżej informacje pozostawiają wiele niepewności, które nie zostały wystarczająco wyjaśnione. Przykładem może być podanie “magicznej” liczby 5 przy opisie testu c2.
Można uzupełnić tę informację dodając, że chodzi tu o warunek przybliżenia rozkładu wielomianowego rozkładem Gaussa. Dlaczego jednak ten właśnie warunek jest tu istotny?
dpowiedź będzie bardziej ogólna. Przedstawione tu ćwiczenie stanowi pojedynczy pomiar, który w ograniczonym tylko zakresie reprezentuje populację możliwych prezentacji poruszonych tu zagadnień. Autorzy będą wdzięczni Czytelnikom za pomoc w odnalezieniu błędów grubych, które zostaną niezwłocznie wyeliminowane oraz niedopatrzeń systematycznych wynikających z profesjonalnych przyzwyczajeń autorów. Najlepiej jednak jest wyznaczyć wartość średnią poprzez uzupełnienie podanych tu wiadomości korzystając z bogatej literatury. Kilka wybranych pozycji podanych będzie poniżej.