W 1999 roku Reka Albert, Hawoong Jeong i Albert-Laszlo Barabasi z Uniwersytetu Notre Dame w Indianie podjęli jedną z pierwszych prób zbadania struktury sieci WWW. Zaprogramowali robota sieciowego (program komputerowy), którego zadaniem było wejść na każdą stronę WWW w domenie ich rodzimego uniwersytetu, odnaleźć wszystkie hiperlinki zamieszczone na tej stronie, zapamiętać ich liczbę i lokalizację (tj. witrynę początkową i tę, na którą badany link wskazuje), a następnie podążyć tymi linkami do innych stron i tam powtórzyć całą procedurę. Błądząc w ten sposób po sieci WWW, robot odwiedził ponad 300 tysięcy dokumentów HTML i prześledził ponad 1,5 miliona połączeń między tymi dokumentami. Najważniejszym wynikiem pomysłowego eksperymentu było odkrycie potęgowych rozkładów prawdopodobieństwa opisujących liczby połączeń wychodzących ze stron WWW, jak również wskazujących na dowolne strony tej sieci.
Zaobserwowany potęgowy rozkład prawdopodobieństwa
|
(3.1) |
opisujący strukturę sieci WWW był dla tych naukowców (i nie tylko dla nich) dużym zaskoczeniem. Oczywiście spodziewano się, że w sieci WWW będzie dużo więcej witryn słabo usieciowionych (z małą liczbą połączeń w obu kierunkach), ale żadną miarą nie oczekiwano, że sieć WWW jest bezskalowa, że mówiąc o niej trzeba unikać sformułowań typu "charakterystyczny, średni stopień". Odkrycie bezskalowości sieci WWW było tym bardziej intrygujące, że nie jest ona tworem, który rozwija się według ściśle narzuconych reguł. Struktura połączeń sieci WWW jest wynikiem indywidualnych decyzji pojedynczych użytkowników, którzy sami określają, ile i jakich odnośników umieścić na tworzonej przez siebie stronie. To z wielości i różnorodności tych lokalnych decyzji wyłania się matematyczne prawo, które jak później pokazano, pozostaje w mocy nie tylko dla stron umieszczonych w domenie Uniwersytetu Notre Dame, ale dla całej ogólnoświatowej sieci WWW.
Wkrótce po odkryciu bezskalowej struktury sieci WWW pokazano, że wiele innych sieci rzeczywistych również wykazuje potęgowy rozkład stopni wierzchołków. Tę cechę zaobserwowano m.in. w Internecie, sieciach telefonii komórkowej i w wielu sieciach społecznych, np. sieci współpracy naukowej, sieci cytowań, a nawet w sieci kontaktów seksualnych. Początkowe zdumienie wszechobecnością sieci bezskalowych szybko zrodziło pytanie, dlaczego tak wiele sieci ma bezskalowy charakter. Gdy pewna cecha pojawia się w wielu systemach niemających ze sobą oczywistego związku, należy podejrzewać, że istnieje wspólna przyczynowa zasada, którą można ująć w najbardziej ogólnych kategoriach, bez odnoszenia się do szczegółów tego czy innego przypadku. Czy zatem bezskalowość sieci złożonych wynika z jakichś uniwersalnych reguł rządzących dynamiką tych układów?
Odpowiedź na to pytanie jest twierdząca, a odkrycie ogólnej reguły ponownie zawdzięczamy naukowcom z Uniwersytetu Notre Dame. To właśnie Albert-Laszlo Barabasi i Reka Albert w swojej legendarnej już pracy pt. Emergence of scaling in random networks, opublikowanej w czasopiśmie "Science" w 1999 roku, pokazali, że potęgowy rozkład stopni wierzchołków w wielu sieciach rzeczywistych jest konsekwencją dwóch komplementarnych mechanizmów: wzrostu sieci i reguły preferencyjnego dołączania węzłów.
Procedura konstrukcyjna ewoluującej sieci Barabasiego-Albert obejmuje następujące etapy:
.
(
) połączeń do istniejących już wierzchołków sieci. Pojawiające się w sieci nowe węzły realizują liniową regułę preferencyjnego dołączania, która polega na tym, że prawdopodobieństwo, że nowy wierzchołek utworzy połączenie do jednego ze starszych węzłów, np. węzła i o stopniu 
, jest wprost proporcjonalne do stopnia tego węzła  |
(3.2) |
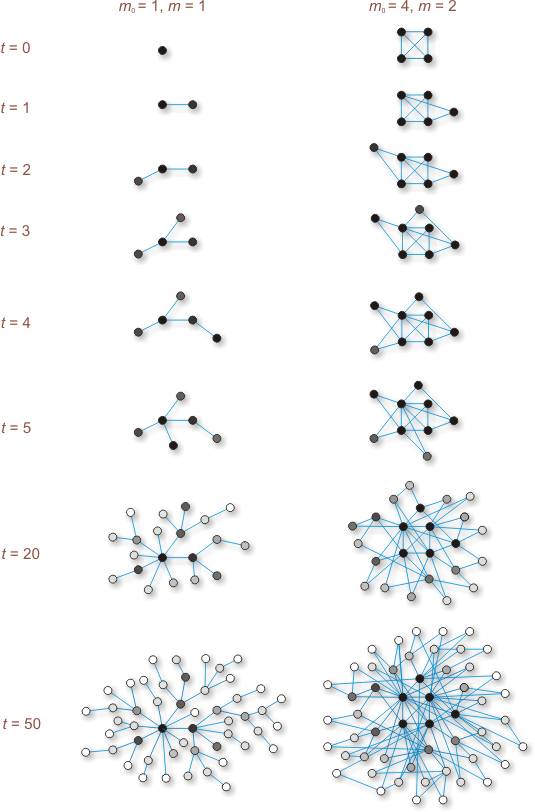
Zajmiemy się teraz wyznaczeniem rozkładu stopni wierzchołków w sieci Barabasiego-Albert. W tym celu posłużymy się tzw. metodą czasu ciągłego, w której oprócz uwypuklonego w nazwie założenia o ciągłości czasu, przyjmuje się, że stopnie 
węzłów badanej sieci również zmieniają się w sposób ciągły, tzn. o ułamki stopnia w każdym kroku czasowym. To drugie założenie powoduje, że w opisywanej metodzie tak naprawdę posługujemy się średnimi wartościami stopni poszczególnych węzłów, a nie ich prawdziwymi wartościami, i to właśnie na podstawie tych średnich stopni wyznaczamy rozkład stopni wierzchołków. Oznacza to, że uzyskany w wyniku tej metody rozkład jest rozkładem uśrednionym. Ścisłą metodę wyznaczenia rozkładu stopni wierzchołków w sieci BA, metodę opartą na równaniu master, omawiamy w dalszej części tego opracowania.
Podstawowe równanie metody czasu ciągłego opisuje, w jaki sposób w czasie zmienia się stopień węzła i. W pojedynczym kroku czasowym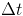 
tempo zmiany stopnia tego węzła, tj.
 |
zależy od tego, ile krawędzi nowego wierzchołka trafia do węzła i. Jeśli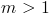 
, nic nie stoi na przeszkodzie temu, by rozważany węzeł zdobył więcej niż jedno połączenie. Prawdopodobieństwo uzyskania l połączeń, tak jak w schemacie Bernoullego, jest opisane rozkładem dwumianowym
 |
(3.3) |
w którym prawdopodobieństwo sukcesu jest wyrażone przez regułę preferencyjnego dołączania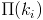 
(3.2).
Przypominamy, że schematem Bernoullego nazywamy ciąg n niezależnych doświadczeń, z których każde może się zakończyć sukcesem (z prawdopodobieństwem p) lub porażką (z prawdopodobieństwem 1-p). Prawdopodobieństwo, że wśród tych n prób odnotujemy k sukcesów (i odpowiednio n-k porażek) jest opisane rozkładem
 |
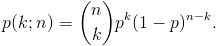(3.4) |
Wartość średnia tego rozkładu jest równa
 |
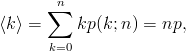(3.5) |
natomiast jego wariancja (kwadrat odchylenia standardowego) wynosi
 |
(3.6) |
Znając prawdopodobieństwo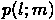 
, tempo zmiany stopnia 
węzła i możemy zapisać w postaci równania
 |
(3.7) |
którego prawa strona jest równa wartości średniej (3.5) rozkładu dwumianowego (3.3). Rozwiązując to równanie różniczkowe przy warunku początkowym 
, gdzie 
jest momentem (krokiem czasowym), w którym węzeł i został dodany do sieci, otrzymujemy zależność
 |
(3.8) |
która mówi, w jaki sposób stopień węzła i zmienia się w czasie, gdy sieć BA rośnie.
Znając zależność (3.8), możemy już wyznaczyć rozkład stopni wierzchołków 
w badanych sieciach. W tym celu korzystamy ze znanej zależności między gęstościami rozkładów prawdopodobieństwa oraz 
dla zmiennych 
oraz 
, między którymi istnieje funkcyjna zależność (3.8)
 |
(3.9) |
Ponieważ nowe węzły w sieci pojawiają się w stałych odstępach czasu, gęstość jest gęstością rozkładu jednorodnego
 |
(3.10) |
Podstawiając (3.8) oraz (3.10) do równania (3.9), otrzymujemy poszukiwany rozkład stopni wierzchołków
 |
(3.11) |
Zauważmy, że uzyskany rozkład jest rozkładem potęgowym. Wykładnik charakterystyczny tego rozkładu ma ustaloną wartość 
(zobacz rysunek). W dalszej części wykładu pokażemy, że proste modyfikacje założeń modelu BA pozwalają uzyskać rozkłady potęgowe o innej wartości tego wykładnika.
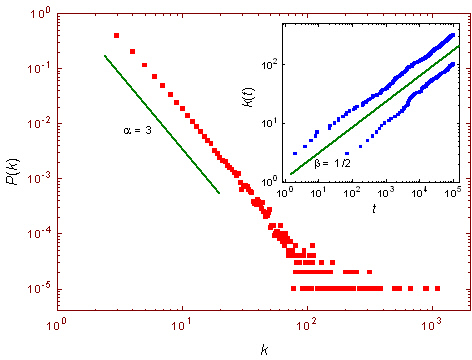
W przeciwieństwie do omówionej wcześniej metody czasu ciągłego, zastosowanie równania master umożliwia ścisłe wyznaczenie tego rozkładu. Jest to możliwe, ponieważ w metodzie równania master od samego początku posługujemy się rozkładem prawdopodobieństwa dla stopni węzłów, nie zaś średnimi stopniami węzłów, tak jak w metodzie czasu ciągłego.
W fizyce statystycznej równanie master (ang. master equation), zwane też równaniem M lub równaniem mistrza, jest równaniem różniczkowym pierwszego rzędu, które opisuje zmianę w czasie prawdopodobieństwa 
tego, że badany układ przebywa w stanie i. Równanie M ma bardzo intuicyjną postać. Zakładając, że w każdej chwili t rozważany układ może zmienić swój stan i na dowolny inny stan j (tj. 
) oraz przyjmując, że tempo takich zmian (tj. prawdopodobieństwo, że zmiana dokona się w jednostce czasu dt) jest równe 
, równanie na zmianę w czasie prawdopodobieństwa można zapisać w postaci
 |
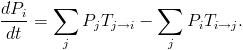(3.12) |
Sumy prawdopodobieństw po prawej stronie tego równania reprezentują dwa konkurujące ze sobą procesy: zmianę dowolnego stanu układu j na interesujący nas stan i (pierwsza suma) oraz zmianę rozważanego stanu i na dowolny, inny stan j (druga suma, wzięta ze znakiem minus).
Niech zatem 
oznacza prawdopodobieństwo, że w chwili t węzeł i dodany do sieci w kroku czasowym ma stopień k. Prawdopodobieństwo to spełnia proste równanie algebraiczne
 |
(3.13) |
które wynika z następującego rozumowania: wiemy, że w pojedynczym kroku czasowym węzeł i może uzyskać l nowych krawędzi, przy czym 
; jeśli w chwili t rozważany węzeł miał stopień k-l (prawdopodobieństwo takiego zdarzenia jest równe 
), wówczas prawdopodobieństwo, że w chwili t+1 uzyska l nowych połączeń i będzie miał stopień k, jest opisane rozkładem dwumianowym 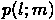(3.4), w którym prawdopodobieństwo sukcesu p jest opisane regułą preferencyjnego dołączania 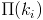(3.2) do węzłów o stopniu k-l. Iloczyn tych prawdopodobieństw, tj. 
, wyraża prawdopodobieństwo, że węzeł o stopniu k-l uzyskuje odpowiednią liczbę nowych połączeń, tj. l; sumując takie iloczyny po l otrzymujemy prawą stronę równania (3.13).
Prawdopodobieństwo opisane równaniem (3.13) odnosi się do pojedynczego węzła. Sumując prawdopodobieństwa odnoszące się do wszystkich węzłów badanej sieci, uzyskujemy rozkład stopni wierzchołków 
charakteryzujący całą sieć BA w chwili t
 |
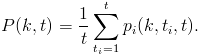(3.14) |
Co więcej, sumując w taki sam sposób obie strony zależności (3.13), otrzymujemy równanie opisujące, w jaki sposób w czasie zmienia się rozkład
 |
(3.15) |
Poniewa ż nas interesuje rozwiązanie tego równania w granicy 
, możemy przyjąć, że czas jest zmienną ciągłą, tj.
 |
(3.16) |
Podstawiając (3.16) do zależności (3.15), otrzymujemy równanie master (3.12) dla rozkładu stopni wierzchołków w ewoluującej sieci BA
 |
(3.17) |
W granicy długich czasów, tj.
 |
(3.18) |
prawa strona równania (3.17) znika i równanie to upraszcza się do rekurencyjnej zależności
 |
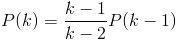(3.19) |
o warunku początkowym
 |
(3.20) |
Rozwiązując tą rekurencję otrzymujemy wyrażenie opisujące rozkład stopni wierzchołków w sieci Barabasiego-Albert
 |
(3.21) |
gdzie 
.
Na koniec zauważmy, że w granicy 
uzyskany rozkład staje się równoważny rozkładowi (3.11) uzyskanemu za pomocą metody czasu ciągłego. Zwracamy jednak uwagę na to, że opisana metoda równania master jest, w przeciwieństwie do wspomnianej metody czasu ciągłego, metodą ścisłą. Wykonując obliczenia prowadzące do równania master wykonaliśmy wprawdzie kilka przybliżeń, ale wynikały one jedynie z poszukiwania granicznej postaci rozkładu prawdopodobieństwa 
dla .