Równowagowe sieci przypadkowe

Klasyczne grafy przypadkowe Erdosa-Renyi (ER)

Procedura konstrukcyjna

Sieci znane obecnie jako klasyczne grafy przypadkowe (lub grafy ER) po raz pierwszy zostały omówione przez wybitnych matematyków węgierskiego pochodzenia Paula Erdosa i Alfreda Renyiego w połowie XX wieku. W ich oryginalnych tych matematyków graf przypadkowy , a ściślej statystyczną zbiorowość tych grafów , definiuje się za pomocą procedury konstrukcyjnej, która obejmuje dwa etapy:

Na początku ustala się liczbę węzłów N należących do grafu.
Następnie spośród wszystkich par węzłów, losowo wybiera się E par, między którymi tworzy się połączenia.

Odtąd określenie klasyczne grafy przypadkowe będziemy stosować do pewnego uogólnienia oryginalnego modelu Erdosa-Renyiego. W tym ogólniejszym modelu klasycznych grafów przypadkowych stały parametr E, określający liczbę krawędzi umieszczonych w sieci, zastąpimy prawdopodobieństwem p istnienia krawędzi między dowolną parą wierzchołków (patrz rysunek). Nowa procedura konstrukcyjna klasycznych grafów przypadkowych będzie zatem obejmowała następujące etapy:

Pierwszy etap, polegający na ustaleniu liczby węzłów N należących do grafu.
Drugi, w którym z zadanym prawdopodobieństwem p będziemy przypisywali połączenie każdej z par węzłów.

Rozkład stopni wierzchołków

Z procedury konstrukcyjnej grafów ER wynika, że rozważane sieci zawierają średnio

(3.47)

krawędzi, skąd na podstawie lematu o uściskach dłoni !!! wnioskujemy, że średni stopień węzła należącego do tych sieci jest równy

(3.48)

Analizując procedurę konstrukcyjną klasycznych grafów przypadkowych, można również wywnioskować, że rozkład stopni wierzchołków w tych gafach jest rozkładem dwumianowym (3.4). Prawdopodobieństwo, że dowolny węzeł uzyska k na N-1 możliwych połączeń do innych wierzchołków sieci, jest równoważne prawdopodobieństwu uzyskania k sukcesów w N-1 próbach, gdy prawdopodobieństwo sukcesu wynosi p, a prawdopodobieństwo porażki 1-p:

(3.49)

Gdy liczba krawędzi (3.47) w grafie jest mała, tzn. gdy , rozkład dwumianowy (3.49) można przybliżyć rozkładem Poissona (zobacz ponizszy rysunek)

(3.50)

w którym parametr jest opisany wyrażeniem (3.48).

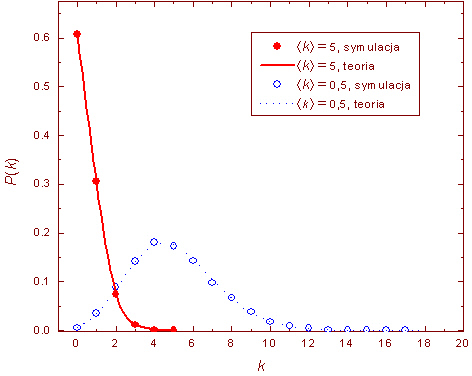
Z uwagi na rozkład (3.50) klasyczne grafy przypadkowe są często określane mianem ,,grafów poissonowskich''. Zwykle to określenie pojawia się w zestawieniu z określeniem ,,sieci potęgowe'' lub ,,bezskalowe'' (czyli sieci o potęgowym rozkładzie stopni wierzchołków ) i służy uwypukleniu jednej z najpoważniejszych wad grafów ER, uniemożliwiającej wykorzystanie tych sieci do modelowania układów rzeczywistych. Oczywiście tą wadą jest wąski, o bardzo małej wariancji rozkład stopni wierzchołków. Przypomnijmy bowiem, że w rozkładzie Poissona wariancja jest równa wartości średniej

(3.51)

Wynika stąd, że odchylenie standardowe stopni węzłów od wartości średniej , jest bardzo małe w porównaniu z tą wartością

(3.52)

Ta cecha rozkładu Poissona sprawia, że węzły o stopniach znacznie różniących się od średniego stopnia wcale się w grafach ER nie pojawiają. Z tego powodu klasyczne grafy przypadkowe można traktować jak grafy regularne, w których wszystkie węzły mają ten sam stopień .

Współczynnik gronowania i efekt małych światów

Poissonowski charakter rozkładu stopni wierzchołków obserwowany w klasycznych grafach przypadkowych nie jest jedyną cechą, która je dyskwalifikuje jako potencjalne modele rzeczywistych sieci złożonych. Kolejną ich wadą jest bardzo mała wartość współczynnika gronowania, zdefiniowanego jako prawdopodobieństwo istnienia połączenia między parą węzłów, które mają już przynajmniej jednego wspólnego sąsiada. Zauważmy, że z uwagi na przyjętą w procedurze konstrukcyjnej omawianych sieci niezależność krawędzi, współczynnik gronowania C charakteryzujący całą sieć ER, a także każdy węzeł tej sieci z osobna , jest równy prawdopodobieństwu istnienia pojedynczej krawędzi, tj.

(3.53)

Ten wynik nie powinien być dla czytelnika zaskoczeniem. W grafach ER krawędzie są niezależne od siebie, a prawdopodobieństwo powstania krawędzi jest takie samo dla wszystkich par węzłów.

Przypomnijmy również, że klasyczne grafy przypadkowe są małymi światami. Średnia odległość między dowolną parą węzłów należących do tych sieci spełnia następującą relację skalowania

(3.54)

Zespół statystyczny klasycznych grafów przypadkowych

Wykład poświęcony klasycznym grafom przypadkowym zakończymy bardzo ogólnym omówieniem własności zbioru (w fizyce statystycznej taki zbiór, rozpatrywany łączenie z rozkładem prawdopodobieństwa , nazywamy przestrzenia fazową, statystyczną zbiorowością, zespołem statystycznym lub po prostu ansamblem klasycznych grafów przypadkowych). Celem tego omówienia jest uświadomienie czytelnikowi, czym tak naprawdę są sieci przypadkowe i jak tę przypadkowość należy rozumieć. Rozpoczęty tu temat będziemy, na bardziej zaawansowanym poziomie, kontynuowali podczas omawiania modelu p*.

Na początek zauważmy, że postępując zgodnie z procedurą konstrukcyjną klasycznych grafów przypadkowych można utworzyć

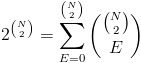(3.55)

różnych realizacji takich grafów. Wyjaśnijmy tylko, że umieszczony po prawej stronie wyrażenia (3.55) symbol Newtona odpowiada liczbie różnych realizacji grafów prostych o ustalonej liczbie krawędzi E, tj. liczbie wszystkich kombinacji E elementowych zbioru elementowego. Sumując symbol Newtona po wszystkich wartościach parametru otrzymujemy liczbę wszystkich możliwych grafów prostych o zadanej liczbie węzłów . Oczywiście, liczba ta odpowiada liczbie różnych, zero-jedynkowych i na dodatek symetrycznych macierzy sąsiedztwa o ustalonym rozmiarze N. Nawet dla niewielkich rozmiarów sieci ta liczba jest ogromna. Na przykład, gdy N=E=100, liczba grafów przypadkowych o tych parametrach jest równa , liczba zaś wszystkich grafów ER o N=100 wierzchołkach wynosi .

Z uwagi na to, że w klasycznych grafach przypadkowych prawdopodobieństwo pojawienia się dowolnej krawędzi jest równe p, poszczególne grafy należące do badanego zbioru mają różne prawdopodobieństwa realizacji . Na przykład dla p=1 jedynym grafem, jaki jesteśmy w stanie uzyskać, postępując zgodnie z opisaną wcześniej procedurą konstrukcyjną, jest graf pełny, w którym każdy węzeł jest połączony z każdym innym węzłem sieci, tzn. . Odpowiednio prawdopodobieństwo realizacji innych grafów jest wtedy równe zeru, tj. dla . Z podobną sytuacją mamy do czynienia, gdy p=0. Wówczas, jedynym grafem o niezerowym prawdopodobieństwie realizacji jest graf pusty. Natomiast, gdy parametr , prawdopodobieństwo realizacji dowolnego spośród grafów przypadkowych o ustalonej liczbie krawędzi E jest równe

(3.56)

To prawdopodobieństwo (3.56) odpowiada równoczesnej realizacji niezależnych zdarzeń, spośród których E zdarzeń (typu jest krawędź) ma prawdopodobieństwo realizacji równe p, natomiast prawdopodobieństwo realizacji pozostałych zdarzeń (typu nie ma krawędzi) jest równe 1-p.

Prawdopodobieństwo opisane wzorem (3.56) można traktować tak samo, jak prawdopodobieństwo pojedynczego mikrostanu w podstawowych rozkładach równowagowej fizyki statystycznej (np. w rozkładzie kanonicznym lub wielkim kanonicznym). Badając pewną wielkość makroskopową charakteryzującą te grafy (np. liczbę krawędzi E), powinniśmy pamiętać, że jest ona funkcją mikrostanu (tzn. ). Wyznaczając charakterystyczną dla badanego zespołu średnią wartość tej wielkości, musimy tę wielkość uśrednić po całej przestrzeni fazowej . Zauważmy na przykład, że odpowiednia wartość średnia parametru E jest opisana wzorem (3.47)

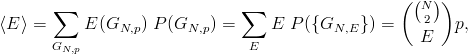(3.57)

gdzie

(3.58)

opisuje prawdopodobieństwo makrostanu o ustalonej liczbie krawędzi E, natomiast funkcja

(3.59)

jest równoważna znanej z fizyki statystycznej funkcji gęstości stanów, która mówi o tym, na ile sposobów można zrealizować grafy proste o N wierzchołkach i E połączeniach.