Elementy teorii grafów

Statystyczne charakterystyki sieci

Rozkład stopni wierzchołków

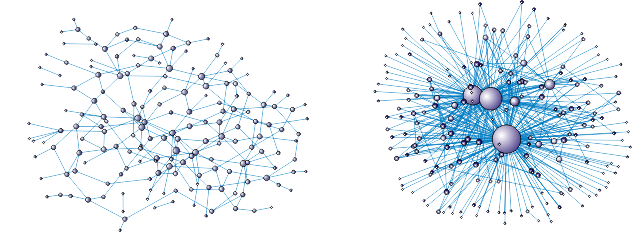
Spójrzmy na rysunek:

Widzimy dwie sieci o tej samej liczbie węzłów N i tej samej liczbie krawędzi E. Rozmiar węzłów w każdej z tych sieci jest proporcjonalny do ich stopni. Tym, co odróżnia od siebie te sieci, jest rozkład stopni wierzchołków P(k). Rozkład ten mówi nam, ile jest w danej sieci węzłów o małej, a ile o dużej liczbie połączeń. Ogólnie, P(k) reprezentuje ułamek wszystkich węzłów w sieci, które mają stopień k. Możemy też powiedzieć, że P(k) opisuje prawdopodobieństwo, że losowo wybrany węzeł będzie miał stopień k.

Choć przez uproszczenie układów rzeczywistych do zbioru węzłów i krawędzi (czyli przedstawienie ich w postaci sieci) tracimy wiele cennych informacji, ma ono wiele zalet. Przede wszystkim, postępując w ten sposób możemy zastosować te same narzędzia analizy do całkiem odmiennych układów. W taki właśnie sposób węgierski fizyk Albert-Laszlo Barabasi dokonał pod koniec ubiegłego wieku zdumiewającej obserwacji. Odkrył on mianowicie, że różne sieci rzeczywiste opisujące całkiem odmienne układy mają pewną uniwersalną własność: rozkład stopni wierzchołków w tych sieciach ma charakter potęgowy (podobnie jak sieć po prawej stronie rysunku):

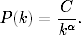(1.1)

Implikacje tego faktu są niezwykle ważne dla funkcjonowania tychże sieci. Na razie przypomnijmy jedynie, że rozkład potęgowy, w odróżnieniu na przykład od rozkładu Gaussa, Poissona czy rozkładu wykładniczego, nie ma naturalnej skali, jest bezskalowy. Oznacza to, że mówienie o średnich wartościach stopni wierzchołków w takich sieciach jest co najmniej niewskazane, a wielu wypadkach posługiwanie się ideą średniego stopnia prowadzi do poważnych błędów. W sieci o potęgowym rozkładzie stopni wierzchołków wiele węzłów ma tylko jedną krawędź, ale można też znaleźć węzły z ogromną liczbą krawędzi, tzw. huby. Ta dysproporcja w niezwykły sposób przekłada się na własności sieci bezskalowych i czyni z nich bardzo ciekawe obiekty badań.

Spójrzmy na rysunek 1.2. Przedstawiliśmy na nim sieć połączeń lotniczych w Stanach Zjednoczonych. Dla porównania pokazaliśmy również sieć połączeń drogowych, w której krawędzie reprezentują autostrady łączące ze sobą większe miasta. Różnice między tymi dwiema sieciami przypominają różnice z rysunku 1.1. W sieci autostrad stopień większości węzłów mieści się w przedziale od 2 do 6, a zwykle wynosi 4. Sytuacji tej odpowiada przedstawiony na rysunku 1.2C rozkład stopni wierzchołków o charakterystycznym dzwonowatym kształcie, przypominającym rozkład normalny lub rozkład Poissona. Kształt rozkładu wykonanego dla sieci połączeń lotniczych jest zupełnie inny. Mówi on, że istnieje bardzo dużo słabo usieciowionych lotnisk o małej liczbie połączeń oraz że istnieje mała liczba węzłów lotniczych, z których można dotrzeć prawie wszędzie. O takim rozkładzie mówimy, że ma tłusty ogon.

Rys. 1.2: Sieć autostrad (A) i sieć połączeń lotniczych (B) w Stanach Zjednoczonych. C – F – rozkłady stopni wierzchołków tych sieci przedstawione w różnych skalach.

Nie wszystkie tłustoogoniaste rozkłady P(k) są rozkładami potęgowymi. Aby to rozstrzygnąć, warto przedstawić badaną zależność P(k) w skali podwójnie logarytmicznej. Okazuje się, że w takiej skali potęgowe rozkłady prawdopodobieństwa mają postać linii prostej. Ta własność rozkładów potęgowych staje się oczywista, gdy obustronnie zlogarytmujemy zależność (1.1)

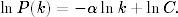(1.2)

Wówczas przedstawiony w nowych współrzędnych, tj. X = lnk, Y = lnP(k), rozkład potęgowy (1.1) staje się równoważny liniowej zależności

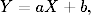(1.3)

gdzie a = −α oraz b = lnC. Na rysunku 1.2E i 1.2F przedstawiono w skali podwójnie logarytmicznej odpowiednio kształt rozkładu z dobrze określoną średnią oraz charakterystyczny kształt rozkładu potęgowego.

Jak wspomnieliśmy, dopiero kilkanaście lat temu odkryto, że potęgowy rozkład stopni wierzchołków jest cechą charakterystyczną ogromnej liczby sieci rzeczywistych. Na rysunku 1.3 przedstawiono trzy przykładowe rozkłady potęgowe zaobserwowane w: sieci współpracy między aktorami, sieci WWW i sieci energetycznej, w której węzłami są stacje transformatorowe, krawędzie zaś reprezentują linie wysokiego napięcia między tymi stacjami.

Rys. 1.3: Rozkład stopni wierzchołków trzech różnych sieci rzeczywistych. A – sieć współpracy między N = 212250 aktorami, <k> = 28,78; B – sieć WWW, N = 325729, <k> = 5,46; C – sieć energetyczna, N = 4941, <k> = 2,7. Linie przerywane mają nachylenia: αA = 2,3, αB = 2,1 oraz αC = 4.

Współczynnik gronowania

W sieciach złożonych krawędź zawsze opisuje pewną prostą relację między parą obiektów. W sieciach społecznych istnienie krawędzi może świadczyć o tym, że ludzie się znają, lubią, kochają lub razem pracują. W wielu wypadkach takie binarne relacje są jednak zbyt upraszczające. Na nasze stosunki z innymi osobami mogą wpływać również osoby trzecie. Z tego powodu socjologowie analizujący interakcje w sieciach społecznych zaczęli badać również stosunki między trzema osobami. Relacje wewnątrz takiego trójkąta (triady) są znacznie bardziej złożone i przez to ciekawsze (patrz rysunek 1.4).

Rys. 1.4: Wszystkie możliwe relacje wewnątrz trzyosobowej grupy w grafie skierowanym.

Układ wzajemnie powiązanych trzech (i więcej) osób można traktować jako małą organizację, której wpływ na funkcjonowanie sieci bywa znaczący. Powstawanie takich triumwiratów w sieciach jest przecież pierwszym etapem do formowania się znacznie bardziej złożonych grup społecznych.

Formowaniu się sieci społecznych, polegającemu na przykład na tworzeniu się nowych znajomości i zanikaniu starych, towarzyszą efekty grupowania (gronowania, klastrowania) się ludzi o podobnych zainteresowaniach i separacji grup o sprzecznych poglądach. Zjawisko to znane jest w socjologii jako teoria równowagi społecznej. Zrozumiałe wydaje się bowiem, że zawiązujemy zwykle przyjaźnie z osobami podobnymi do nas samych. Fakt ten socjologia określa mianem homofilii, w znaczeniu upodobania do podobieństwa. Nakazuje ona jednostce obracanie się wśród osób, które są do niej podobne poglądami, zainteresowaniami, zawodem itp. Podobnie zrozumiałe jest, że unikamy relacji konfliktowych. Istnienie trójkąta, w którym dwie osoby nie cierpią się wzajemnie i jednocześnie przyjaźnią z tą samą trzecią osobą, prowadzi co najmniej do dyskomfortu wewnątrz takiej triady¹. Ludzie mają silniejszą tendencję do budowania przyjaźni z przyjaciółmi swoich przyjaciół. Oznacza to, że jeśli osoba ma dwoje przyjaciół, to z dużym prawdopodobieństwem i oni zaprzyjaźnią się ze sobą, tworząc stabilny trójkąt.

Jak widzimy, analiza gronowania może nam dostarczyć wielu informacji o sieci. W celu analizy tych efektów wprowadzono definicję współczynnika gronowania. W najprostszej postaci dotyczy ona grafów prostych i jest miarą liczby krawędzi w otoczeniu badanego wierzchołka.

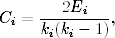(1.6)

gdzie 0 ≤ E_i ≤ k_i(k_i − 1) / 2, dzięki czemu 0 ≤ C_i ≤ 1. Jak widzimy, współczynnik gronowania opisuje prawdopodobieństwo, że pierwsi sąsiedzi węzła i są względem siebie również pierwszymi sąsiadami. Prosty przykład obliczania współczynnika gronowania został przedstawiony na rysunku 1.5.

Rys. 1.5: Najbliższe otoczenie wierzchołka i. Ciągłymi liniami oznaczono istniejące krawędzie. Przerywane linie oznaczają nieistniejące, lecz możliwe krawędzie. Aby obliczyć współczynnik gronowania środkowego (białego) węzła, należy podzielić liczbę istniejących krawędzi między jego sąsiadami Ei = 1 przez liczbę wszystkich możliwych połączeń między nimi = 3. Stąd Ci = 1∕3.

Współczynnik gronowania całej sieci jest po prostu wartością C_i (1.6) uśrednioną po wszystkich węzłach

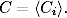(1.7)

Współczynnik gronowania grafu pełnego (czyli takiego, w którym są wszystkie możliwe krawędzie) wynosi 1. W grafach pustych współczynnik ten jest z definicji równy 0. Warto również wiedzieć, że istnieje wiele innych definicji współczynników gronowania. Jedną z nich, szczególnie popularną w socjologii, jest definicja współczynnika gronowania w postaci

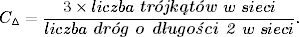(1.8)

Czynnik 3 w liczniku wyrażenia (1.8) wynika z faktu, iż w jednym trójkącie istnieją trzy drogi o długości 2 – każda prowadząca przez inny środkowy węzeł.

Choć oba wyrażenia (1.7) i (1.8) mówią o liczbie trójkątów w sieciach, to należy zdawać sobie sprawę, że w większości wypadków dają one inne wyniki. Przede wszystkim dzieje się tak wtedy, gdy lokalny współczynnik gronowania C_i zależy od stopnia węzła i, a jak pokażemy za chwilę, w sieciach rzeczywistych taka zależność występuje bardzo często. Na razie przeanalizujmy najprostszy przykład niezgodności obu definicji. Rozważmy sieć

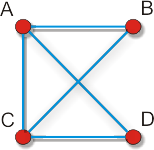
złożoną z czterech wierzchołków i pięciu krawędzi. Lokalne współczynniki gronowania C_i (1.6) węzłów A, B, C i D wynoszą odpowiednio 2∕3, 1, 2∕3 oraz 1. Oznacza to, że dla całej sieci C = (2∕3 + 1 + 2∕3 + 1)∕4 = 5∕6. Znajdźmy teraz wartość współczynnika C_Δ. W sieci mamy dwa trójkąty ABC i ACD oraz osiem dróg o długości 2: BAC, DAC, BAD, ACD, ACB, BCD, ABC oraz ADC. Współczynnik gronowania liczony według wzoru (1.8) wyniesie C_△ = 3 * 2∕8 = 3∕4, czyli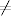 C_△C.

Zbadajmy teraz wartość współczynnika gronowania w całkowicie przypadkowej sieci, złożonej z N węzłów połączonych w losowy sposób E krawędziami. W takiej sieci każda para wierzchołków jest połączona z tym samym prawdopodobieństwem <k>∕N, gdzie średni stopień <k> = 2E∕N. Wspomnieliśmy wcześniej, że współczynnik gronowania reprezentuje prawdopodobieństwo istnienia bezpośredniego połączenia między dwoma sąsiadami danego wierzchołka. W naszej sieci przypadkowej to prawdopodobieństwo jest takie samo dla wszystkich węzłów niezależnie od tego, czy są one sąsiadami tego samego węzła, czy nie. Wynika stąd, że C = <k>∕N. Dla dużych sieci, w których <k> << N, wartość współczynnika gronowania jest bliska zeru.

Okazuje się, że w większości sieci rzeczywistych współczynnik gronowania ma wysoką wartość, na przykład w Internecie C = 0,18 ÷ 0,30, w sieci językowej (współwystępowania wyrazów) C = 0,7, a w sieci aktorów C = 0,79. W tabeli 1.2 przedstawiono współczynniki gronowania kilkunastu przebadanych sieci rzeczywistych.

Wśród tych sieci znajdują się również nieomówione przez nas dotychczas sieci współpracy między naukowcami (patrz na przykład rysunek 1.6). W takich sieciach krawędź miedzy dwoma węzłami (naukowcami) oznacza wspólną pracę (artykuł, raport) naukową, o której informacja znajduje się w danej bazie, na przykład LANL, SPIRES, MEDLINE itp. W większości wypadków współczynnik gronowania tych sieci należy do przedziału od 0,4 do 0,7. Wyjątek stanowi baza danych MEDLINE, gromadząca informacje na temat publikacji z dziedziny medycyny, w której C = 0,066. Jakkolwiek wysoki współczynnik gronowania wśród naukowców nie powinien nikogo dziwić, ponieważ pracują w zespołach kilkuosobowych, publikują w podobnych czasopismach, poznają współpracowników swoich współpracowników na różnych konferencjach, to odmienny charakter współpracy w medycynie wydaje się zaskakujący. Wyjaśnienia tej obserwacji można szukać w sposobie organizacji pracy w laboratoriach medycznych. W zespołach takich istnieje zwykle jeden lider, gromadzący wokół siebie dużą liczbę studentów, doktorantów i techników pracujących nad odmiennymi projektami i nie mających niemal możliwości współpracy. Powstała w wyniku tych mechanizmów współpracy sieć ma strukturę lokalnie drzewiastą, w której liczba trójkątów jest znikomo mała, a co za tym idzie, współczynnik gronowania jest niski.

Sieci małych światów

W eksperymencie przeprowadzonym w 1967 roku amerykański socjolog Stanley Milgram wysłał do przypadkowo wybranych ludzi 160 listów zawierających wyjaśnienie eksperymentu, zdjęcie, nazwisko i adres pewnej osoby oraz instrukcję postępowania. Jeżeli adresat znał osobiście człowieka wymienionego w liście, miał przesłać list bezpośrednio do niego. W przeciwnym wypadku list powinien zostać przesłany do innego znajomego, o którym adresat mógł sądzić, że może znać poszukiwaną osobę lub przynajmniej znać kogoś, kto tę osobę zna osobiście. Celem eksperymentu było ustalenie, jak długi jest łańcuch znajomych gwarantujący dostarczenie przesyłki do adresata.

Choć większość listów zaginęła, to jednak te 42, które dotarły do poszukiwanej osoby, dostarczyły zaskakujących wyników. Okazało się, że paru listom wystarczyło zaledwie dwóch pośredników by dotrzeć do celu. W kilku innych przypadkach pośredników było kilkunastu. Jednak, po uśrednieniu wyników, okazało się, że statystyczny list przeszedł przez ręce jedynie sześciu osób.

Eksperyment Milgrama dowiódł prawdziwości obiegowego porzekadła (znanego również Barneyowi), że świat jest mały. Mimo że sieć społeczna liczy kilka miliardów ludzi, to średnia droga między dowolną parą węzłów w takiej sieci wynosi około sześciu. Ponad dwadzieścia lat po eksperymencie Milgrama ukute zostało nawet sformułowanie „sześć uścisków dłoni” albo „sześć stopni separacji”. Nie ważne, czy jesteś aborygenem, Eskimosem, czy Tybetańczykiem. Od każdej osoby na świecie dzieli cię średnio właśnie sześć uścisków dłoni.

Eksperyment Milgrama został powtórzony w ostatnich latach przez naukowców z Microsoftu przy wykorzystaniu Internetu. Amerykanie Eric Horvitz i Jure Leskovec przeanalizowali wirtualne trasy 30 mld wiadomości, które zostały wysłane w czerwcu 2006 roku z 240 mln komputerów z całego świata. Okazało się, że przeciętnie pomiędzy dwoma dowolnymi użytkownikami znajduje się około 6,6 ogniw pośredniczących.

Idea sześciu stopni separacji w szczególny sposób wpłynęła również na popularność pewnego amerykańskiego aktora Kevina Bacona. Aktor ten w filmach gra bezustannie od 1978 r. i prawdę mówiąc, wystąpił w tak wielu produkcjach, że teoretycznie znajduje się w samym centrum sieci aktorów. Opierając się na tej obserwacji, wymyślono grę towarzyską polegającą na zaproponowaniu najkrótszej drogi łączącej wymienionego aktora z Kevinem Baconem. Długość tej drogi ochrzczono mianem liczby Bacona. Większość aktorów charakteryzuje się liczbą Bacona równą 2 lub 3 (patrz na przykład rysunek 1.9. Sprawdź liczbę swojego ulubionego aktora w Wyroczni Bacona!).

W matematyce, odpowiednikiem liczby Bacona jest liczba Erdősa. Paul Erdős, jeden z twórców nauki o sieciach złożonych, zasłynął również z powodu nadzwyczaj intensywnej współpracy z innymi naukowcami. W sieci, w której węzłami są naukowcy, a połączenie oznacza wspólną publikację, stopnień wierzchołka odpowiadającego Erdosowi wynosi ponad 500. Średnia droga w takiej sieci jest krótsza niż 5, a większość naukowców ma liczbę Erdősa mniejszą niż 8. Na przykład Albert Einstein ma tę liczbę równą 2, natomiast wykładowcy naszego Wydziału Agata Fronczak -2 oraz Piotr Fronczak -3.

Wszystkie powyższe przykłady świadczą o tym, że sieci społeczne słusznie zasługują na nazwę małych światów. Jednakże inne rodzaje sieci złożonych również mają podobne właściwości: średnia odległość między dwoma dowolnymi wierzchołkami jest w tych sieciach mała w porównaniu z liczbą wierzchołków, mimo że zwykle są to sieci rzadkie, tzn. liczba krawędzi jest niewiele większa od liczby wierzchołków (w odróżnieniu od sieci gęstych, gdzie E ~ N²).

Nawet w największej z przedstawionych sieci, sieci WWW, złożonej z ponad 200 milionów węzłów, średnia droga wynosi zaledwie 16. Oznacza to, że wystarczy średnio 16 kliknięć myszą, aby przejść z dowolnej strony internetowej na dowolną inną stronę.

Miary centralności

Średnia odległość

Aby bardziej formalnie określić małość świata, wartość średniej drogi w badanej sieci porównuje się ze średnią drogą w najprostszym modelu sieci złożonej, jakim jest graf przypadkowy (graf z losowo rozmieszczonymi krawędziami). Zapiszmy średnią najkrótszą drogę (czyli średnią odległość) jako

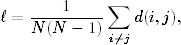(1.11)

gdzie d(i,j) jest najkrótszą drogą między wierzchołkami i oraz j. Okazuje się, że w grafie przypadkowym

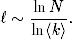(1.12)

Ta logarytmiczna zależność pokazuje, jak mało zależy średnia odległość od rozmiaru sieci w sieciach złożonych. Dla porównania w sieciach opartych na siatce kwadratowej ℓ ~ .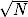

W 1998 roku Watts i Strogatz zaproponowali, aby traktować sieć jako mały świat pod warunkiem, że typowe odległości w takiej sieci są porównywalne z odległościami w grafie przypadkowym. Większość znanych sieci złożonych spełnia ten warunek. Wyjątkiem jest sieć połączeń energetycznych, w której średnia droga jest zbyt duża, by sieć ta zasługiwała na miano małego świata. Tym co ją wyróżnia spośród innych, jest jej planarny charakter², który uniemożliwia bezpośrednie połączenie na przykład między stacją transformatorową w Nowym Jorku i w Los Angeles.

Okazuje się, że sieciach bezskalowych o potęgowym rozkładzie stopni wierzchołków zależność średniej odległości od rozmiaru sieci jest jeszcze słabsza. W sieciach, w których wykładnik charakterystyczny α > 3,

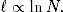(1.13)

Gdy wykładnik α = 3, mamy natomiast

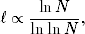(1.14)

gdy zaś α należy do przedziału (2,3), w sieciach bezskalowych obserwujemy tzw. efekt ultramałych światów

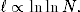(1.15)

Pośrednictwo

Twierdzenie, że sprawność przekazu informacji zależy tylko od odległości między nadawcą a odbiorcą, nie jest słuszne. Informacja przekazywana z węzła do węzła może przecież utknąć gdzieś po drodze, w węźle, który nie radzi sobie z jej szybkim przetwarzaniem. Z tego powodu węzły pośredniczące w przekazie informacji mogą mieć znaczenie strategiczne i należałoby określić ich wpływ na jakość transmisji danych.

Miarą ważności (centralności) takich węzłów jest tzw. pośrednictwo (ang. betweenness). Idea tej miary oparta jest na założeniu, że komunikacja odbywa się tylko wzdłuż najkrótszych dróg.

Jest ona zatem równa

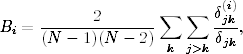(1.17)

gdzie k,ji. Aby znaleźć na przykład pośrednictwo wierzchołka A na przedstawionej poniżej sieci

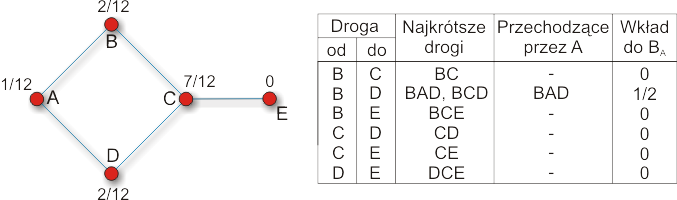
należy przeanalizować wkład każdej z najkrótszych dróg między pozostałymi wierzchołkami. Okazuje się, że przyczynek do pośrednictwa wnosi tylko jedna z dwóch najkrótszych dróg z wierzchołka B do D.

Pośrednictwo ma prostą interpretację jako miara wpływu wierzchołka na odporność sieci na uszkodzenia. Mówi ono mianowicie, jak wiele najkrótszych dróg stracimy, gdy usuniemy węzeł z sieci. Innymi słowy, aby skutecznie zakłócić działanie sieci, powinniśmy uszkodzić te węzły, których pośrednictwo jest największe.

Zamiast uszkadzać węzły, możemy też przecinać połączenia międzywęzłowe. W tym wypadku należy zdefiniować pośrednictwo w odniesieniu do krawędzi e

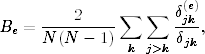(1.18)

gdzie δ_jk^(e) jest liczbą najkrótszych dróg przechodzących przez krawędź e.

Aby uzmysłowić sobie znaczenie idei pośrednictwa węzłów i krawędzi w sieciach złożonych, rozważmy sieć oddziaływań między proteinami. W sieci takiej dwie proteiny są połączone krawędzią, jeśli jedna z nich ma wpływ na funkcjonowanie drugiej. Silnie usieciowione proteiny mają wpływ na wiele procesów wewnątrzkomórkowych, jednakże to nie stopień protein okazuje się kluczowy dla funkcjonowania tej sieci.

Na rysunku 1.11 przedstawiono sieć oddziaływań między proteinami w drożdżach. Enzym Cak1p (tzw. kinaza cyklino-zależna), przedstawiony w środkowej części rysunku, jest ogniwem dwóch szlaków przekazywania sygnałów w komórce. Z jednej strony, aktywuje on inny enzym Cdc28p, który jest ważnym regulatorem cyklu komórkowego. Z drugiej strony, Cak1p aktywuje również Smk1p, kinazę biorącą udział w procesie morfogenezy (zarodnikowania). Oprócz tych dwóch protein Cak1p ma tylko dwóch innych sąsiadów w sieci oddziaływań (YDR279W i Sgv1p), co daje mu całkowity stopień równy zaledwie 4. Nie jest to więc hub (jak na przykład proteina Cdc28p). Jednakże jego kluczowe położenie w sieci sprawia, że ma ogromny wpływ na funkcjonowanie komórki. Uszkodzenie tego węzła może prowadzić na przykład do niekontrolowanego dzielenia się komórki, raka i śmierci organizmu (Cak1 jest bliskim odpowiednikiem CDK6 – genu odpowiedzialnego za choroby nowotworowe u ludzi)⁷ .

Na koniec chcielibyśmy również zaznaczyć, że w sieciach o potęgowym rozkładzie stopni wierzchołków rozkład pośrednictwa węzłów ma także charakter potęgowy

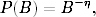
(1.19)

przy czym wykładnik charakterystyczny tego rozkładu η zwykle ma wartość bliską 2 (dla sieci o potęgowym rozkładzie stopni wierzchołków z wykładnikiem 2 < γ ≤ 3). Na rysunku 1.12 przedstawiono rozkłady pośrednictwa węzłów w wybranych sieci rzeczywistych.

¹W fizyce magnetyków takie układy nazywa się sfrustrowanymi.