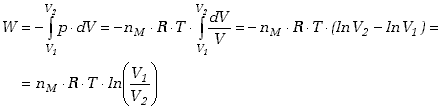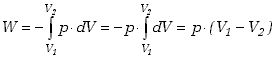Podstawowe procesy cieplne

 Rozważmy kilka podstawowych procesów cieplnych (termodynamicznych).

Przemiana izochoryczna

Proces, w którym objętość układu pozostaje stała, czyli 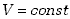, nazywamy przemianą izochoryczną. W przemianie tej układ nie wykonuje pracy nad otoczeniem, więc w oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację

,

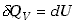 (7.18)

co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła.

 

Pojemność cieplna substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem 

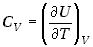
 (7.19)

gdzie indeks przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P.Joule'a z rozprężaniem rozrzedzonego gazu do próżni gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła  z otoczeniem. Możemy wiec zapisać wzór (7.19) dla gazu doskonałego w postaci

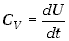
 (7.20)
czyli w dowolnym procesie kwazistatycznym, odwracalnym niezależnie jaka wielkość jest stała zmiana energii wewnętrznej 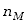moli gazu doskonałego jest określona wzorem .

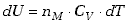
(7.21)

Przemiana izotermiczna

Jeśli dany proces zachodzi w stałej temperaturze, czyli 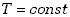, to mówimy, że zachodzi przemiana izotermiczna. Z równania stanu gazu wynika natychmiast, że w przemianie tej ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości, bowiem dla danej masy gazu wyrażonej w molach mamy 

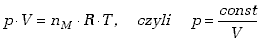
(7.22)

Związek ten zwany jest prawem Boyle'a Mariotte'a.

 
 

Pracę wykonaną nad układem przy przemianie izotermicznej  wyznaczamy w oparciu o definicję (7.9) oraz korzystając z równania stanu dla przemiany izotermicznej (7.22).

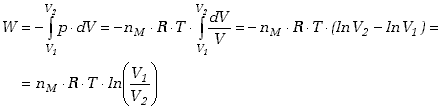
 (7.23)

Zapiszmy pierwsza zasadę termodynamiki dla przemiany izotermicznej w postaci różniczkowej, wzór (7.8)

.

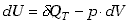 (7.24)

W przemianie izotermicznej T=const, więc dU=0 . Oznacza to, że w przemianie tej układ ma ciągle taką samą energię wewnętrzną. Widzimy dalej, że mimo iż temperatura układu jest stała, to jest wymieniane ciepło między układem i otoczeniem. Ilość tego ciepła możemy określić w oparciu o równanie (7.24)

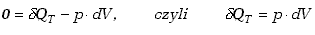
 (7.25)

 co określa, uwzględniając zmianę znaku, wyrażenie (7.23). Jeśli praca jest wykonywana nad układem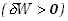 , to ciepło w równej ilości musi być oddawane do otoczenia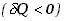i  vice versa.

Przemiana izobaryczna

Jeśli proces zachodzi pod stałym ciśnieniem, czyli 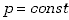, to mówimy, że zachodzi przemiana izobaryczna. Układ wykonuje dodatnią prace nad otoczeniem W'- rozszerzając się lub ujemną - kurcząc się. Ciśnienie zachowuje stałą wartość więc praca wykonana nad układem w przemianie izobarycznej wynosi

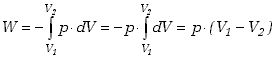
 (7.26)

 Podwyższenie temperatury o jeden stopień wymaga więcej ciepła niż w przypadku ogrzewania bez zmiany objętości, bowiem część ciepła zużywana jest na wykonanie pracy. 

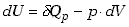
 (7.27)

Wyrażenie to możemy przepisać w innej postaci wykorzystując wzór (7.20)

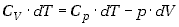
 (7.28)

gdzie wprowadziliśmy pojęcie ciepła molowego przy stałej objętości 

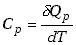
 (7.29)

Z równania (7.28) wynika, że w procesie izobarycznym zmieniają się wszystkie funkcje termodynamiczne, a więc energię wewnętrzna możemy zmienić zarówno na drodze wykonania pracy jak i wymiany ciepła.

Różniczkując równanie stanu gazu dla procesu izobarycznego, gdzie 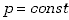mamy

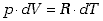
 (7.30)

Wykorzystując ten związek możemy równanie (7.28) przepisać, po podzieleniu przez 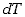, w postaci

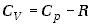
 (7.31)

Stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości stanowi charakterystykę danego gazu i oznaczany jest zwykle symbolem 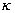(kappa). 

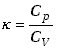
 (7.32)

Wykorzystując wzór (7.31) mamy związek

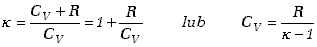
 (7.33)