"Philosophiae naturalis principia mathematica"
w postaci trzech zasad dynamiki.
Zasady te omówimy teraz bardziej szczegółowo.
Fot.3.2. Na fotografii - Issaac Newton (1642 -
1727) - figura w gabinecie figur woskowych Mme Tussaud w Lonndynie
(WiŻ,
5/1977,s.28)
Pierwsza zasada dynamiki
|
Zapiszmy pierwsza zasadę dynamiki w sposób podobny do oryginalnego sformułowania Newtona.
Zasadniczą wartością pierwszej zasady dynamiki jest wprowadzenie równoważności stanu spoczynku i stanu ruchu jednostajnego prostoliniowego. Układy, w których pierwsza zasada dynamiki jest spełniona, nazywamy układami inercjalnymi; układy, w których spełniona nie jest - układami nieinercjalnymi. |
Rozpatrzmy to na przykładzie ruchu pociągów. Kiedy siedzimy w przedziale wagonu jadącego pociągu, układem nieruchomym jest dla nas wagon, bo względem nas się nie porusza. Kiedy stoimy na peronie, układem nieruchomym jest stacja kolejowa. Oba te układy odniesienia są jednakowo dobre do badania stanu ruchu innych przedmiotów, jeśli tylko w czasie prowadzenia obserwacji prędkość pociągu pozostaje stała co do wartości i kierunku. Pierwsza zasada dynamiki mówi, że kiedy pociąg zmienia stan swego ruchu, to musiała zostać wywarta na niego jakaś siła - w przeciwnym wypadku jego stan ruchu (lub bezruchu) pozostawałby bez zmian.
Sytuacja jest zasadniczo inna, kiedy pociąg nasz rusza lub zatrzymuje się - kiedy zmienia wartość lub kierunek swej prędkości. Znajdując się w takim pociągu nie jesteśmy w stanie wypowiadać się o ruchu innych obiektów (pociągów), bo nie wiemy czy to nasz, czy obserwowany przez nas pociąg zmienia stan swego ruchu. Układ taki nie jest dobrym układem odniesienia i jest w sprzeczności z pierwsza zasadą dynamiki.
Jadący pociąg może być układem inercjalnym ale tylko wtedy gdy wektor jego prędkości zachowuje stałą wartość. Zauważmy, że kiedy znany jest jeden układ inercjalny, to znanych jest ich nieskończenie wiele. Każdy bowiem układ poruszający się względem układu inercjalnego z dowolną ale stałą co do wartości i kierunku prędkością jest też układem inercjalnym. Pierwsza zasada dynamiki stanowi wiec definicję układu inercjalnego.
| Newton określił masę jako
miarę ilości
materii uważając tę jej właściwość za niezależną od stanu ruchu
obiektów materialnych.
Jednostkę masy (kilogram, kg) wprowadziliśmy już. Zdefiniowaliśmy też pojęcie punktu materialnego. Teraz,
każdemu
obiektowi materialnemu przypiszemy masę |
Kiedy interesuje nas ruch układu wielu punktów materialnych, wprowadzamy
pojęcie środka masy. Wektor położenia środka masy
dla układu ![]() punktów związany jest z masami
punktów związany jest z masami ![]() oraz promieniami wodzącymi
oraz promieniami wodzącymi ![]() wszystkich punktów wchodzących w skład układu wzorem
wszystkich punktów wchodzących w skład układu wzorem
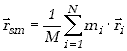 , ,
| gdzie | 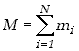
| (3.1) |
|---|
Kiedy rozpatrujemy ruch obiektu o ciągłym rozkładzie masy, określamy położenie jego środka masy podobnie jak dla układu punktów materialnych, ale sumowanie zastępujemy całkowaniem, wykorzystując znane z matematyki określenie całki oznaczonej.
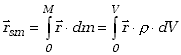
| gdzie | 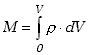 . .
| (3.2) |
|---|
Wprowadzoną tu wielkość
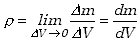
| (3.3) |
|---|
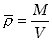 . .
| (3.4) |
|---|
|
Dla ilościowego opisu ruchu ciała o danej masie wprowadza się pojęcie wektora pędu zdefiniowanego jako iloczyn masy ciała i wektora jego prędkości. Pęd jest więc także wektorem, a jego kierunek zgodny jest z kierunkiem wektora prędkości.
|
Pęd układu punktów materialnych stanowi wektorową sumę pędów wszystkich punktów wchodzących w jego skład
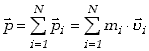
| (3.6) |
|---|
Pęd układu może być wyrażony przez pęd jego środka masy. Różniczkując bowiem lewy z wzorów (3,1) względem czasu - otrzymujemy
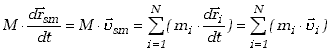
| (3.7) |
|---|
gdzie przy różniczkowaniu skorzystaliśmy z założenia, że masa zachowuje wartość stałą w czasie ruchu. Pochodne wektorów wodzących względem czasu oznaczyliśmy następnie symbolami prędkości.
Wzór (3,7) można teraz przepisać wyrażając pędu układu punktów materialnych poprzez pęd środka masy
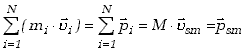
| (3.8) |
|---|
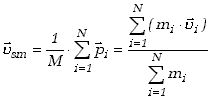
| (3.9) |
|---|
Kiedy ciało jest pod działaniem sił nie równoważących się wzajemnie, to zgodnie z pierwszą zasadą dynamiki jego stan spoczynku lub ruchu jednostajnego prostoliniowego ulega zmianie - zmienia się wektor jego prędkości. Intuicyjnie wyczuwamy, że zmiana prędkości będzie tym większa, im większa siła będzie na ciało działać oraz, że kierunek zmiany prędkości będzie zgodny z kierunkiem działania siły. Z doświadczenia wiemy też, że większą siłę trzeba przykładać do ciał o większej masie niż o mniejszej, by osiągnąć tą samą zmianę prędkości.
|
Druga zasady dynamiki wyraża związek pomiędzy zmianą w czasie pędu ciała, a siłą pod wpływem której zmiana ta zachodzi.
Zmianę pędu w czasie wyrażamy jako pochodną pędu względem czasu otrzymując wzór wyrażający ilościowo drugą zasadę dynamiki
|
Pochodna pędu względem czasu oznacza szybkość zmiany pędu. Możemy wiec drugą zasadę dynamiki sformułować także następująco:
|
Druga zasada dynamiki |
|
Szybkość zmiany pędu ciała równa jest wpadkowej sile działającej na to ciało. |
W ten sposób druga zasada dynamiki daje nam ilościowe określenie siły.
Jeśli przyjmiemy, że masa ciała podczas ruchu pozostaje stała, to równanie (2) możemy przepisać w postaci
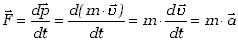
| (3.10a) |
|---|
gdzie ![]() jest
wektorem przyspieszenia ciała.
jest
wektorem przyspieszenia ciała.
|
Druga zasada dynamiki może więc być także sformułowana inaczej.
Założenie o stałości masy nie zawsze jest jednak spełnione. Pierwsze sformułowania drugiej zasady dynamiki są więc ogólniejsze od tego ostatniego. |
W przypadku układu punktów materialnych możemy zapisać drugą zasadę dynamiki do każdego z punktów oddzielnie, a następnie utworzyć sumę takich równań otrzymując
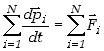 . .
| (3.11) |
|---|
Z drugiej strony, poprzez zróżniczkowanie stronami względem czasu wyrażenia (3,8) możemy otrzymać zależność
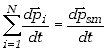 . .
| (3.12) |
|---|
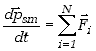 . .
| (3.13) |
|---|
Wzór ten zawiera bardzo ważną informację pokazując, że środek masy układu punktów materialnych porusza się tak, jakby działała na niego wypadkowa wszystkich sił działających na poszczególne punkty materialne układu. Sformułowanie to można jeszcze doprecyzować, ale w tym celu musimy zapoznać się z trzecią zasadą dynamiki.
|
Domowe Laboratorium
Fizyczne |
||
|
Na zaczepionej u góry nici zawieszony jest arbuz. U dołu przymocowana jest taka sama druga nić. )===>>> |
|
Kasia wykonuje doświadczenie. Będzie ciągnąć za nić zaczepioną u dołu. |
| Odpowiedz - która nić, dolna czy górna, zerwie się kiedy Kasia pociągnie szybko, a która - kiedy będzie ciągnąć powoli. Uzasadnij swoją odpowiedź. Teraz zobacz wynik doświadczenia. | ||
Zapiszmy inaczej wzór (3.10a). Kiedy na ciało o masie ![]() działamy siłą
działamy siłą ![]() ,
nadajemy mu przyspieszenie
,
nadajemy mu przyspieszenie
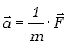 . .
| (3.14) |
|---|
|
Masa i ciężar ciała to nie to samo. Masa, która jest własnością danego ciała zwana jest też masą bezwładną w odróżnieniu od ciężaru ciała, który jest różny na Ziemi, na Księżycu lub w statku kosmicznym. Masa bezwładna jest współczynnikiem proporcjonalności w równaniu (3.10a). Ciężar ciała będący siłą jaka działa na ciało wskutek przyciągania grawitacyjnego, jest proporcjonalny do jego masy bezwładnej. Ciężar ciała możemy wyrazić za pomocą równania (3.10a) jako
Jednostką siły w układzie SI jest
niuton
(N). Jest to siła, która masie równej jednej jednostce masy (kilogram)
nadaje przyspieszenie równe jednej jednostce przyspieszenia (1 m/s2);
|
Przyspieszenie ![]() zwane jest przyspieszeniem ziemskim
i nie zależy od własności
spadających przedmiotów, ale od masy Ziemi i odległości danego ciała od środka
jej masy. Dlatego też inna jest wartość tego przyspieszenia na biegunie, inna
na równiku, bowiem Ziemia nie jest idealną kulą; inna jest także nad
powierzchnią Ziemi.
Oczywiście, można też podobnie zdefiniować przyspieszenie na Księżycu,
Marsie itd.
zwane jest przyspieszeniem ziemskim
i nie zależy od własności
spadających przedmiotów, ale od masy Ziemi i odległości danego ciała od środka
jej masy. Dlatego też inna jest wartość tego przyspieszenia na biegunie, inna
na równiku, bowiem Ziemia nie jest idealną kulą; inna jest także nad
powierzchnią Ziemi.
Oczywiście, można też podobnie zdefiniować przyspieszenie na Księżycu,
Marsie itd.
|
Różnice pomiędzy pomiarami masy i ciężaru demonstrują wagi: szalkowa i sprężynowa. |
|
|
|
Z pomocą wagi szalkowej dokonujemy pomiaru przez
porównanie ciężaru ważonego przedmiotu z ciężarem odważnika o danej masie.
Kiedy szalki są w równowadze, ciężary obu przedmiotów są równe, ponieważ
równe są ich masy, co wynika z wzoru (3.15). Warunek równowagi nie zależy tu od
wartości g. Wartość ta musi być jedynie różna od zera i taka
sama dla obydwu szalek. Inaczej jest w przypadku wagi sprężynowej. Tu ciężar przedmiotu równoważony jest siłą sprężyny. Wielkość ściśnięcia sprężyny zależy zarówno od wartości zawieszonej na haczyku masy m, jak i od wartości przyspieszenia grawitacyjnego g. Mierzy się wartość ciężaru, który jest iloczynem obu tych wielkości, wzór (3.15). Wynik pomiaru w przypadku wagi sprężynowej będzie więc różny na Ziemi i Księżycu, bo różne są wartości g, a będzie taki sam dla wagi szalkowej, bo wynik od wartości g nie zależy. Czy jednak można wykonać te pomiary w przestrzeni kosmicznej? Jeśli nie, to jak tam zmierzyć masę ciała? |
Druga zasada dynamiki stanowi fundament całej fizyki klasycznej. W niezwykle prostej postaci wzoru (3.2) zawarte są prawa ruchu obiektów materialnych poczynając od przykładowego wazonu spadającego z szafy, a kończąc na ruchu samolotów, rakiet i ciał niebieskich. Zasada ta wyznacza związek pomiędzy przyczyną (siła) i skutkiem jej działania (przyspieszenie) stanowiąc podstawę deterministycznego rozumienia praw fizyki wyrażanego przez tzw. zasadę przyczynowości. Zgodnie z tą zasadą znajomość warunków początkowych (położeń i prędkości ciał w danej chwili czasu) oraz działających na te ciała sił wyznacza jednoznacznie stan ich ruchu w dowolnej chwili czasu. Zakres stosowalności drugiej zasady dynamiki wyznaczony został dopiero w początkach XX-go wieku poprzez mechanikę relatywistyczna i kwantową. Zasada ta jest jednak szczególnym przypadkiem obu tych teorii fizycznych.
Widzimy więc, że siły zawsze występują parami. (uświadomił nam to Newton w trzeciej zasadzie dynamiki), ale są przyłożone do różnych ciał. Zwróćmy uwagę, że gdyby były przyłożone do jednego ciała, to znosiłyby się i w naszym świecie nie byłoby ruchów zmiennych.
|
|
| Fot.3.3. Przeciąganie liny jest typowym przykładem akcji i reakcji. (WiŻ, 6/2000,s.57) |
Zastosujmy trzecią zasadę dynamiki do układu punktów materialnych. Przyjmijmy, że na każdy z punktów działają różnorodne siły pochodzące od innych punktów oraz z zewnątrz i zapiszmy dla i-go punktu, reprezentującego dowolny punkt układu, drugą zasadę dynamiki w postaci
|
| (3.17) |
|---|
gdzie górnym indeksem (w) oznaczyliśmy siły pochodzące od innych punktów układu, a indeksem (z) siły zewnętrzne działające na dany punkt. Sumując obustronnie wyrażenia (3,17) dla wszystkich punktów układu otrzymamy
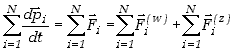
| (3.18) |
|---|
Zauważmy jednak, że zgodnie z trzecią zasadą dynamiki, jeśli jeden punkt układu oddziałuje na drugi, to drugi działa na pierwszy z tą samą siłą, ale przeciwnie skierowaną. Suma sił działających na i-ty punkt pochodzi od pozostałych (N-1) punktów układu. Kiedy zsumujemy te siły, to każdej ze składowych sił będzie odpowiadać inna - przeciwnie skierowana. Suma wszystkich sił wewnętrznych wyniesie więc zero.
Teraz możemy doprecyzować wzór (3,11) eliminując z niego składową związaną z siłami wewnętrznymi.
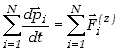
| (3.19) |
|---|
Wzór (3,13) możemy teraz przepisać w postaci
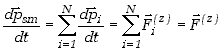
| (3.20) |
|---|
Sens fizyczny tego wzoru możemy sformułować w postaci ważnego stwierdzenia.
Środek masy układu punktów materialnych porusza się
tak, jak poruszałby się punkt materialny gdyby działała na niego wypadkowa
siła ![]() wszystkich
zewnętrznych sił działających na wszystkie punkty układu.
wszystkich
zewnętrznych sił działających na wszystkie punkty układu.
Sformułowanie to odnosi się także i do ciała sztywnego, które możemy traktować jako sumę nieskończonej liczby punktów materialnych. Wzór ten stanowi uogólnienie drugiej zasady dynamiki na układ punktów materialnych i ciała sztywne.