| Te symboliczne grające skrzypce mają nam przypominać, że zjawiska, którymi będziemy zajmować się w tej lekcji pozostają w ścisłym związku z poznanymi w kursie Fizyka I drganiami harmonicznymi układów mechanicznych. Związek ten tkwi przede wszystkim w takiej samej postaci równań różniczkowych opisujących zarówno drgania w układach mechanicznych jak i w układach elektrycznych. |
Rysunki poniżej obrazują zmiany zachodzące w obwodzie elektrycznym złożonym z pojemności i indukcyjności. Małe wahadełko w dolnej części rysunków pokazuje to samo, ale dla układu mechanicznego.
|
|
 |
 |
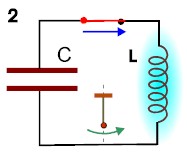
(1) W "chwili zero" kondensator jest naładowany i cała energia układu LC jest energią elektryczną skupioną pomiędzy jego okładkami. (Wahadełko jest odchylone w lewo i cała jego energia jest energią potencjalną.) Wyłącznik ustawiamy w pozycję "włączone". (Puszczamy wahadełko w ruch.) Prąd zaczyna płynąc w obwodzie.
(2) W rezultacie przepływu prądu rośnie pole magnetyczne w solenoidzie, ale kondensator rozładowuje się (Wahadełko uzyskuje energię kinetyczną i traci potencjalną.) Ładunek na okładkach kondensatora staje się równy zeru. Znika energia elektryczna kondensatora, ale nie oznacza to zniknięcia prądu, który określony jest przez dq/dt. Prąd ten płynąc przez solenoid wytwarza w nim pole magnetyczne. Cała energia układu LC jest teraz energią magnetyczną skupioną w solenoidzie. (Wahadełko jest w dolnym położeniu i prędkość jego jest maksymalna. Cała energia wahadełka jest energią kinetyczną.)
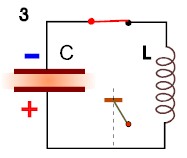
(3) Przepływający prąd naładował kondensator, ale teraz polaryzacja elektrod jest przeciwna. (Wahadełko jest znów w górnym położeniu ale z przeciwnej strony.)
Oczywiście, cykl powtarza się i ruch trwa dalej, jeśli w obwodzie nie występują opory elektryczne (lub mechaniczne). W tej lekcji zobaczymy zarówno cechy wspólne drgań harmonicznych jak i ich specyfikę w układach elektrycznych. Podane tu podstawowe informacje stanowią jedynie wstęp do złożonej analizy zmiennych przebiegów elektrycznych stanowiących podstawę elektroenergetyki oraz elektroniki.
Rozpocznijmy od zapisania prawa Ohma dla obwodu elektrycznego składającego się z pojemności, indukcyjności i oporności, Rys.12.4.1.
|
|
(12.4.1) |
Gdzie stosujemy następujące, znane nam już, przyporządkowania:
|
|
(12.4.2) |
Uwaga wstępna: Wykorzystując prawo Ohma do prądów zmiennych będziemy
zakładać, że wartości prądu we wszystkich miejscach obwodu są w każdej
chwili takie same. Prądy takie nazywamy kwazistacjonarnymi. Założenie
takie jest słuszne dla częstotliwości drgań do ok. 106 Hz. Pamiętajmy
też, że w dalszym ciągu tej lekcji różnicę potencjałów oznaczać będziemy
symbolem U, a symbolem ![]() oznaczać
będziemy fazę drgań obwodu.
oznaczać
będziemy fazę drgań obwodu.
|
|
Kondensator jest naładowany, ale klucz K
jest otwarty . Odpowiada to rozciągnięciu sprężyny,
struny w instrumencie muzycznym lub odchylaniu od pionu wahadła. (Zauważmy
jednak, że energię moglibyśmy przekazać do obwodu także inaczej, np.
umieszczając indukcyjność w zmiennym polu magnetycznym.)
Następnie zwieramy klucz, co powoduje rozładowanie kondensatora C poprzez oporność R i indukcyjność L. |
| Rys.12.4.1. Obwód RLC |
Zapiszemy prawo Ohma wykorzystując podane wyżej przyporządkowania. Suma spadków napięć (z uwzględnieniem znaku) na wszystkich elementach obwodu równa jest zeru, co zapisujemy w postaci zależności
|
|
(12.4.3) |
Dzieląc przez L i pamiętając, że I=dq/dt otrzymujemy równanie różniczkowe
|
|
(12.4.4) |
Jest to zasadnicze równanie drgań w obwodzie, składającym się z podstawowych elementów elektrycznych: oporności R, indukcyjności L i pojemności C.
| Obwód taki zwany jest często
obwodem RLC. Równanie to odpowiada równaniu drgań harmonicznych
znanemu z kursu mechaniki, jeśli dokonamy przyporządkowania: odchylenie
od położenia równowagi, x |